Euler–Fokker genus

In music theory and tuning, an Euler–Fokker genus (plural: genera), named after Leonhard Euler and Adriaan Fokker,[1] is a musical scale in just intonation whose pitches can be expressed as products of some of the members of some multiset of generating prime factors. Powers of two are usually ignored, because of the way the human ear perceives octaves as equivalent.

Euler genus {3, 5} as rectangle
Euler genus {3, 3, 5} as parallelepiped
Euler genus {3, 5, 5} as parallelepiped
Euler–Fokker genus {3, 3, 7} as rectangular parallelepiped

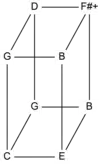
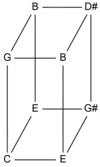
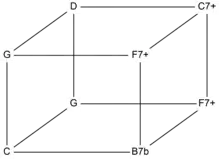
An x-dimensional tone-dimension contains x factors. "An Euler-Fokker genus with two dimensions may be represented in a two-dimensional (rectangular) tone-grid, one with three dimensions in a three-dimensional (block-shaped) tone-lattice. Euler-Fokker genera are characterized by a listing of the number of steps in each dimension. The number of steps is represented by a repeated mention of the dimension, so that there arise descriptions such as [3 3 5 5], [3 5 7], [3 3 5 5 7 7 11 11], etc."[1] For example, the multiset {3, 3, 7} yields the Euler–Fokker genus [3, 3, 7], which contains these pitches:

       1
   3  =3
     7=7
 3×3  =9
   3×7=21
 3×3×7=63

Normalized to fall within an octave, these become: 1/1, 9/8, 21/16, 3/2, 7/4, 63/32. Play 

Euler genera are generated from the prime factors 3 and 5, whereas an Euler–Fokker genus can have factors of 7 or any higher prime number. The degree is the number of intervals which generate a genus. However, not all genera of the same degree have the same number of tones since [XXXYYY] may also be notated [XxYy], "the degree is thus the sum of the exponents," and the number of pitches is obtained adding one to each exponent and then multiplying those ((X+1)×(Y+1)=Z).[2]

Adriaan Fokker wrote much of his music in Euler–Fokker genera expressed in 31-tone equal temperament. Alan Ridout also used Euler-Fokker genera.[2]

Complete contracted chord

The Euler–Fokker genus may also be called a complete contracted chord. Euler coined the term complete chord, while Fokker coined the entire term.[2]

A complete chord has two pitches, the fundamental and a guide tone, the guide tone being a multiple of the fundamental. In between are other pitches which can be seen either as multiples of the fundamental or as divisors of the guide tone (otonality and utonality). For example, given 1 as fundamental and choosing 15 as guide tone, one obtains: 1:3:5:15 (genus [35]). The quotient of the guide tone divided by the fundamental is the "tension number" or "exponens" (Euler: Exponens consonantiae).[2]

List of Euler genera
Second degree
Genera Notes
33 1/1 9/8 3/2
35 1/1 5/4 3/2 15/8
55 1/1 5/4 25/16
Third degree
Genera Notes
333 1/1 9/8 3/2 27/16
335 1/1 9/8 5/4 45/32 3/2 15/8
355 1/1 75/64 5/4 3/2 25/16 15/8
555 1/1 5/4 25/16 125/64
Fourth degree
Genera Notes
3333 1/1 9/8 81/64 3/2 27/16
3335 1/1 135/128 9/8 5/4 45/32 3/2 27/16 15/8
3355 1/1 9/8 75/64 5/4 45/32 3/2 25/16 27/16 225/128 15/8
3555 1/1 75/64 5/4 375/256 3/2 25/16 15/8 125/64
5555 1/1 625/512 5/4 25/16 125/64

...

See also

Sources
  1. Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. ISBN 978-90-5755-065-2.
  2. "What is an Euler–Fokker genus?", Huygens-Fokker.org.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.