Types of mesh

A mesh is a representation of a larger geometric domain by smaller discrete cells. Meshes are commonly used to compute solutions of partial differential equations and render computer graphics, and to analyze geographical and cartographic data. A mesh partitions space into elements (or cells or zones) over which the equations can be solved, which then approximates the solution over the larger domain. Element boundaries may be constrained to lie on internal or external boundaries within a model. Higher-quality (better-shaped) elements have better numerical properties, where what constitutes a "better" element depends on the general governing equations and the particular solution to the model instance.

Common cell shapes

Two-dimensional

Basic two-dimensional Cell shapes

There are two types of two-dimensional cell shapes that are commonly used. These are the triangle and the quadrilateral.

Computationally poor elements will have sharp internal angles or short edges or both.

Triangle

This cell shape consists of 3 sides and is one of the simplest types of mesh. A triangular surface mesh is always quick and easy to create. It is most common in unstructured grids.

Quadrilateral

This cell shape is a basic 4 sided one as shown in the figure. It is most common in structured grids.

Quadrilateral elements are usually excluded from being or becoming concave.

Three-dimensional

Basic three-dimensional cell shapes

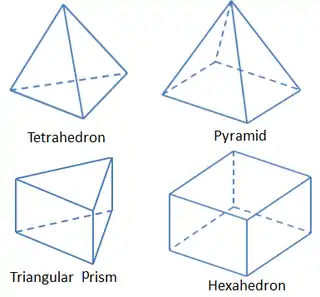
The basic 3-dimensional element are the tetrahedron, quadrilateral pyramid, triangular prism, and hexahedron. They all have triangular and quadrilateral faces.

Extruded 2-dimensional models may be represented entirely by the prisms and hexahedra as extruded triangles and quadrilaterals.

In general, quadrilateral faces in 3-dimensions may not be perfectly planar. A nonplanar quadrilateral face can be considered a thin tetrahedral volume that is shared by two neighboring elements.

Tetrahedron

A tetrahedron has 4 vertices, 6 edges, and is bounded by 4 triangular faces. In most cases a tetrahedral volume mesh can be generated automatically.

Pyramid

A quadrilaterally-based pyramid has 5 vertices, 8 edges, bounded by 4 triangular and 1 quadrilateral face. These are effectively used as transition elements between square and triangular faced elements and other in hybrid meshes and grids.

Triangular prism

A triangular prism has 6 vertices, 9 edges, bounded by 2 triangular and 3 quadrilateral faces. The advantage with this type of layer is that it resolves boundary layer efficiently.

Hexahedron

A hexahedron, a topological cube, has 8 vertices, 12 edges, bounded by 6 quadrilateral faces. It is also called a hex or a brick.[1] For the same cell amount, the accuracy of solutions in hexahedral meshes is the highest.

The pyramid and triangular prism zones can be considered computationally as degenerate hexahedrons, where some edges have been reduced to zero. Other degenerate forms of a hexahedron may also be represented.

Advanced Cells (Polyhedron)

A polyhedron (dual) element has any number of vertices, edges and faces. It usually requires more computing operations per cell due to the number of neighbours (typically 10).[2] Though this is made up for in the accuracy of the calculation.

Classification of grids

Structured grid

Unstructured grid

Structured grids

Structured grids are identified by regular connectivity. The possible element choices are quadrilateral in 2D and hexahedra in 3D. This model is highly space efficient, since the neighbourhood relationships are defined by storage arrangement. Some other advantages of structured grid over unstructured are better convergence and higher resolution.[3] [4] [5]

Unstructured grids

An unstructured grid is identified by irregular connectivity. It cannot easily be expressed as a two-dimensional or three-dimensional array in computer memory. This allows for any possible element that a solver might be able to use. Compared to structured meshes, this model can be highly space inefficient since it calls for explicit storage of neighborhood relationships. These grids typically employ triangles in 2D and tetrahedral in 3D. [6]

Hybrid grids

A hybrid grid contains a mixture of structured portions and unstructured portions. It integrates the structured meshes and the unstructured meshes in an efficient manner. Those parts of the geometry that are regular can have structured grids and those that are complex can have unstructured grids. These grids can be non-conformal which means that grid lines don’t need to match at block boundaries. [7]

Mesh quality

A mesh is considered to have higher quality if a more accurate solution is calculated more quickly. Accuracy and speed are in tension. Decreasing the mesh size always increases the accuracy but also increases computational cost.

Accuracy depends on both discretization error and solution error. For discretization error, a given mesh is a discrete approximation of the space, and so can only provide an approximate solution, even when equations are solved exactly. (In computer graphics ray tracing, the number of rays fired is another source of discretization error.) For solution error, for PDEs many iterations over the entire mesh are required. The calculation is terminated early, before the equations are solved exactly. The choice of mesh element type affects both discretization and solution error.

Accuracy depends on both the total number of elements, and the shape of individual elements. The speed of each iteration grows (linearly) with the number of elements, and the number of iterations needed depends on the local solution value and gradient compared to the shape and size of local elements.

Solution precision

A coarse mesh may provide an accurate solution if the solution is a constant, so the precision depends on the particular problem instance. One can selectively refine the mesh in areas where the solution gradients are high, thus increasing fidelity there. Accuracy, including interpolated values within an element, depends on the element type and shape.

Rate of convergence

Each iteration reduces the error between the calculated and true solution. A faster rate of convergence means smaller error with fewer iterations.

A mesh of inferior quality may leave out important features such as the boundary layer for fluid flow. The discretization error will be large and the rate of convergence will be impaired; the solution may not converge at all.

Grid independence

A solution is considered grid-independent if the discretization and solution error are small enough given sufficient iterations. This is essential to know for comparative results. A mesh convergence study consists of refining elements and comparing the refined solutions to the coarse solutions. If further refinement (or other changes) does not significantly change the solution, the mesh is an "Independent Grid."

Deciding the type of mesh

Skewness based on equilateral volume

If the accuracy is of the highest concern then hexahedral mesh is the most preferable one. The density of the mesh is required to be sufficiently high in order to capture all the flow features but on the same note, it should not be so high that it captures unnecessary details of the flow, thus burdening the CPU and wasting more time. Whenever a wall is present, the mesh adjacent to the wall is fine enough to resolve the boundary layer flow and generally quad, hex and prism cells are preferred over triangles, tetrahedrons and pyramids. Quad and Hex cells can be stretched where the flow is fully developed and one-dimensional.

Depicts the skewness of a quadrilateral

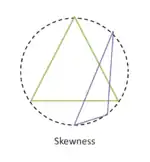
Based on the skewness, smoothness, and aspect ratio, the suitability of the mesh can be decided. [8]

Skewness

The skewness of a grid is an apt indicator of the mesh quality and suitability. Large skewness compromises the accuracy of the interpolated regions. There are three methods of determining the skewness of a grid.

Based on equilateral volume

This method is applicable to triangles and tetrahedral only and is the default method.

${\displaystyle {\text{ Skewness }}={\frac {\text{ optimal cell size - cell size }}{\text{optimal cell size}}}}$

Smooth and large jump change

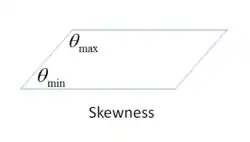
Based on the deviation from normalized equilateral angle

This method applies to all cell and face shapes and is almost always used for prisms and pyramids

${\displaystyle {\text{ Skewness ( for a quad ) }}=\max {\left[{\frac {\theta _{max}-90}{90}},{\frac {90-\theta _{min}}{90}}\right]}}$

Equiangular skew

Another common measure of quality is based on equiangular skew.

${\displaystyle {\text{ Equiangle Skew }}=\max {\left[{\frac {\theta _{max}-\theta _{e}}{180-\theta _{e}}},{\frac {\theta _{e}-\theta _{min}}{\theta _{e}}}\right]}}$

where:

${\displaystyle \theta _{max}\,}$ is the largest angle in a face or cell,

${\displaystyle \theta _{min}\,}$ is the smallest angle in a face or cell,

${\displaystyle \theta _{e}\,}$ is the angle for equi-angular face or cell i.e. 60 for a triangle and 90 for a square.

A skewness' of 0 is the best possible one and a skewness of one is almost never preferred. For Hex and quad cells, skewness should not exceed 0.85 to obtain a fairly accurate solution.

Depicts the changes in aspect ratio

For triangular cells, skewness should not exceed 0.85 and for quadrilateral cells, skewness should not exceed 0.9.

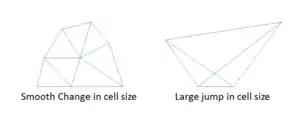
Smoothness

The change in size should also be smooth. There should not be sudden jumps in the size of the cell because this may cause erroneous results at nearby nodes.

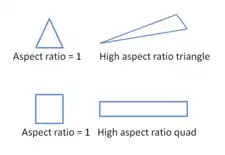
Aspect ratio

It is the ratio of longest to the shortest side in a cell. Ideally it should be equal to 1 to ensure best results. For multidimensional flow, it should be near to one. Also local variations in cell size should be minimal, i.e. adjacent cell sizes should not vary by more than 20%. Having a large aspect ratio can result in an interpolation error of unacceptable magnitude.

Mesh generation and improvement

See also mesh generation and principles of grid generation. In two dimensions, flipping and smoothing are powerful tools for adapting a poor mesh into a good mesh. Flipping involves combining two triangles to form a quadrilateral, then splitting the quadrilateral in the other direction to produce two new triangles. Flipping is used to improve quality measures of a triangle such as skewness. Mesh smoothing enhances element shapes and overall mesh quality by adjusting the location of mesh vertices. In mesh smoothing, core features such as non-zero pattern of the linear system are preserved as the topology of the mesh remains invariant. Laplacian smoothing is the most commonly used smoothing technique.

See also

• Periodic Table of the Finite Elements
• Mesh generation
• Unstructured grid
• Regular grid
• Stretched grid method

References

1. Hexahedron elements
4. Castillo, J.E. (1991), "Mathematical aspects of grid Generation", Society for Industrial and applied Mathematics, Philadelphia
5. George, P.L. (1991), Automatic Mesh Generation
6. Mavriplis, D.J. (1996), "Mesh Generation and adaptivity for complex geometries and flows", Handbook of Computational Fluid Mechanics
7. Bern, Marshall; Plassmann, Paul (2000), "Mesh Generation", Handbook of Computational Geometry. Elsevier Science
8. "Meshing,Lecture 7". Andre Bakker. Retrieved 2012-11-10.