Square pyramid

In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has C_4v symmetry. If all edges are equal, it is an equilateral square pyramid,[1] the Johnson solid J₁.

Square pyramid
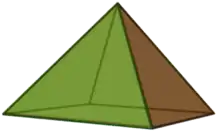Type	Johnson J92 – J1 – J2
Faces	4 triangles 1 square
Edges	8
Vertices	5
Vertex configuration	4(3^2.4) (3^4)
Schläfli symbol	( ) ∨ {4}
Symmetry group	C4v, [4], (*44)
Rotation group	C4, [4]^+, (44)
Dual polyhedron	self
Properties	convex
Net

3D model of a square pyramid

General square pyramid

A possibly oblique square pyramid with base length l and perpendicular height h has volume:

${\displaystyle V={\frac {1}{3}}l^{2}h}$.

Right square pyramid

In a right square pyramid, all the lateral edges have the same length, and the sides other than the base are congruent isosceles triangles.

A right square pyramid with base length l and height h has surface area and volume:

${\displaystyle A=l^{2}+l{\sqrt {l^{2}+(2h)^{2}}}}$

${\displaystyle V={\frac {1}{3}}l^{2}h}$.

The lateral edge length is:

${\displaystyle {\sqrt {h^{2}+{{l^{2}} \over {2}}}}}$,

and the slant height is:

${\displaystyle {\sqrt {h^{2}+{{l^{2}} \over {4}}}}}$.

The dihedral angles are:

between the base and a side: ${\displaystyle \arctan \left({{2\,h} \over {l}}\right)}$;

between two sides: ${\displaystyle \arccos \left({{-l^{2}} \over {l^{2}+4\,h^{2}}}\right)}$.

Equilateral square pyramid, Johnson solid J₁

If all the edges have the same length, then the sides are equilateral triangles, and the pyramid is an equilateral square pyramid, Johnson solid J₁.

The Johnson square pyramid can be characterized by a single edge length parameter l.

The height h (from the midpoint of the square to the apex), the surface area A (including all five faces), and the volume V of an equilateral square pyramid are:

${\displaystyle h={\frac {1}{\sqrt {2}}}l}$

${\displaystyle A=(1+{\sqrt {3}})l^{2}}$

${\displaystyle V={\frac {\sqrt {2}}{6}}l^{3}.}$

The dihedral angles of an equilateral square pyramid are:

• Between the base and a side:

${\displaystyle \arctan {{\biggl (}{\sqrt {2}}{\biggl )}}\approx 54.73561^{\circ }.}$

• Between two (adjacent) sides:

${\displaystyle \arccos {\biggl (}{-1 \over 3}{\biggl )}\approx 109.47122^{\circ }.}$

Graph

A square pyramid can be represented by the Wheel graph W₅.

Related polyhedra and honeycombs

Regular pyramids
Digonal	Triangular	Square	Pentagonal	Hexagonal	Heptagonal	Octagonal	Enneagonal	Decagonal...
Improper	Regular	Equilateral		Isosceles

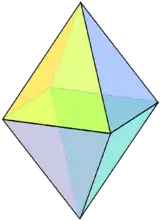
A regular octahedron can be considered a square bipyramid, i.e. two Johnson square pyramids connected base-to-base.	The tetrakis hexahedron can be constructed from a cube with short square pyramids added to each face.	Square frustum is a square pyramid with the apex truncated.

Square pyramids fill space with tetrahedra, truncated cubes or cuboctahedra.[2]

Dual polyhedron

The square pyramid is topologically a self-dual polyhedron. The dual edge lengths are different due to the polar reciprocation.

Dual Square pyramid	Net of dual

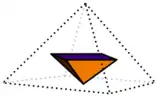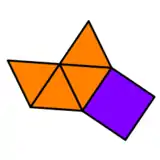References

1. Franz Hocevar, Solid Geometry, 1903, p. 44
2. http://woodenpolyhedra.web.fc2.com/JohnsonHoneycomb.pdf

External links

• Eric W. Weisstein, Square pyramid (Johnson solid) at MathWorld.
• Weisstein, Eric W. "Wheel graph". MathWorld.
• Square Pyramid -- Interactive Polyhedron Model
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra (VRML model)