Identity (music)

In post-tonal music theory, identity is similar to identity in universal algebra. An identity function is a permutation or transformation which transforms a pitch or pitch class set into itself. Generally this requires symmetry. For instance, inverting an augmented triad or C4 interval cycle, 048, produces itself. Performing a retrograde operation upon the tone row 01210 produces 01210. Doubling the length of a rhythm while doubling the tempo produces a rhythm of the same durations as the original.

For other uses, see Limit (music) § Identity.
048 equals itself when transposed by 4 or 8 or when inverted
Sum-4 family (Play ) and interval-4 family (Play )
Sum-4 family and interval-4 family in the chromatic circle, symmetry easily seen
Sum-3 family and interval-3 family for comparison

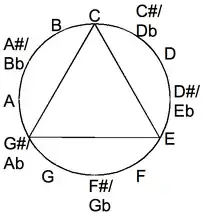
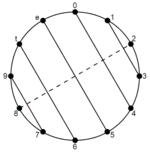
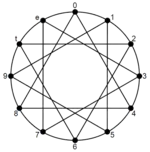
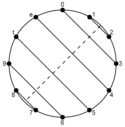
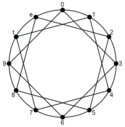
In addition to being a property of a specific set, identity is, by extension, the "family" of sets or set forms which satisfy a possible identity. These families are defined by symmetry, which means that an object is invariant to any of various transformations; including reflection and rotation.

George Perle provides the following example:[1]

"C-E, D-F♯, E♭-G, are different instances of the same interval [interval-4]...[an] other kind of identity...has to do with axes of symmetry [reflection symmetry rather than interval families' rotational symmetry]. C-E belongs to a family [sum-4] of symmetrically related dyads as follows:"
D C♯ C B A♯ A G♯
D D♯ E F F♯ G G♯
2 1 0 e 9 8 7
+ 2 3 4 5 6 7 8
4 4 4 4 4 4 4

C=0, so in mod12, the interval-4 family:

C C♯ D D♯ E F F♯ G G♯ A A♯ B
G♯ A A♯ B C C♯ D D♯ E F F♯ G
0 1 2 3 4 5 6 7 8 9 t e
− 8 9 10 11 0 1 2 3 4 5 6 7
4 4 4 4 4 4 4 4 4 4 4 4

Thus, in addition to being part of the sum-4 family, C-E is also a part of the interval-4 family (in contrast to sum families, interval families are based on difference).

See also

Sources
  1. Perle, George (1995). The Right Notes: Twenty-Three Selected Essays by George Perle on Twentieth-Century Music, p.237-238. ISBN 0-945193-37-8.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.