Flamenco mode

In music theory, the flamenco mode (also Major-Phrygian) is a harmonized mode or scale abstracted from its use in flamenco music. In other words the collection of pitches in ascending order accompanied by chords represents the pitches and chords used together in flamenco songs and pieces. The key signature is the same as that of the Phrygian mode (on E: no accidentals; on C: four flats), with the raised third and seventh being written in as necessary with accidentals. Its modal/tonal characteristics are prominent in the Andalusian cadence.

The two possibilities for ascent and descent over the tonic in the flamenco mode Play : a chromatic tetrachord (E–F–G♯–A) and/or Phrygian tetrachord (E–F–G–A) Play .

There are three fundamental elements which can help define whether or not something really is flameco: A flamenco mode -or musical tonality-; the compás -rhythm- and the performer...who should be a Flamenco! ...For example, if a composer writes a song using a flamenco key- usually called a mode- [without the other two elements then the composer] won't be writing a flamenco piece.[1]

Flamenco, which is a harmonic system of false relations constitutes, according to Manuel de Falla, "one of the marvels of natural art." Only the flamenco guitar, de Falla noted, "can flexibly adjust itself to the ornate melodic embellishments [including melismas] of the flamenco mode."[2]

Flamenco mode Play .

The exact chords depend on the song form (palo) and guitar chord positions[3] since chord voicings in flamenco often include nontriadic pitches, especially open strings.[4] It is characteristic that III, ♭II, and I appear as dissonant chords with a minimum of four tones[3] (for example seventh chords or mixed third chord). Since the tetrachord beginning on the tonic may ascend or descend with either G-sharp or natural (Phrygian tetrachord) the mixed-thirds clash between the major third degree (G♯) in the melody and the minor third degree (G♮) in the accompanying harmony occurs frequently and is characteristic of the flamenco esthetic, as with the blues scale on a major chord.[5]

Augmented sixth chord: B7♭5/F—E or ♭II4
2 —I Play .
Flamenco style melismas from the first movement of Cassadó's Sonata for Cello (1925), m.29-30,[6] cello part (the figure first appears in the piano in measures 1 and 3) (Play )
Flamenco mode with two Phrygian tetrachords Play , also known as the Gypsy minor scale.[7]

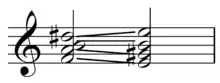
This tetrachord may be copied in the second, producing a D♯ and allowing an augmented sixth chord on the second degree: B7♭5/F.[8]

Lou Harrison composed a "Sonata in Ishartum" (1974 or 1977),[9] which has been arranged by Tolgahan Çoğulu (2001),[10] part of his Suite. In early scholarship regarding a Babylonian cuneiform inscription tuning tablet from the eighteenth century BC., "Ishartum" was equated with the modern Phrygian but is now considered equivalent to the Ionian mode/major scale.[11] Çoğulu's arrangement, at least, is the white note mode on E in Pythagorean tuning, as follows (Play ): F-, C-, G-, D-, A, E, B (F♯+, C♯+, G♯+), or E (1/1), F- (256/243), G- (32/27), A (4/3), B (3/2), C- (128/81), D (16/9), E (2/1), with G♯+ being 81/64.[12]

See also

Sources
  1. Martinez, Emma (2011). Flamenco: All You Wanted to Know, p.6. Mel Bay. ISBN 9781609744700.
  2. George, David (1969). The Flamenco Guitar: From Its Birth in the Hands of the Guitarrero to Its Ultimate Celebration in the Hands of the Flamenco Guitarist, p.111. Society of Spanish Studies. [ISBN unspecified].
  3. Fernández, Lola (2005). Flamenco Music Theory: Rhythm, Harmony, Melody, Form, p.77. ISBN 84-609-3514-0.
  4. Tenzer, Michael (2006). Analytical Studies in World Music, p.97. ISBN 0-19-517789-4.
  5. Fernández (2005), p.78.
  6. Kaufman, Gabrielle (2016). Gaspar Cassadó: Cellist, Composer and Transcriber, p.134. Taylor & Francis. ISBN 9781317130963.
  7. Michale, Ulrich (1982). Atlas de Músical, p.87. cited in Fernández (2005), p.79.
  8. Fernández (2005), p.79.
  9. Josephson, David Lou Harrison: Sonata in Ishartum; Music for Solo Guitar performed by David Tanenbaum at Other Minds 8, 2002", archive.org.
  10. Greve, Martin (2018). Makamsiz: Individualization of Traditional Music on the Eve of Kemalist Turkey, p.187. Ergon Verlag. ISBN 9783956503719.
  11. Alves, Bill and Campbell, Brett (2017). Lou Harrison: American Musical Maverick, p.515, n.12. Indiana University Press. ISBN 9780253026439.
  12. Çoğulu, Tolgahan (Apr 14, 2010). Lou Harrison - Sonata in Ishartum - Pythagorean Tuning / Microtonal Guitar on YouTube "The piece is in "Pythagorean Tuning" with pure fifths."
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.