Fisher's z-distribution

Fisher's z-distribution is the statistical distribution of half the logarithm of an F-distribution variate:

${\displaystyle z={\frac {1}{2}}\log F}$

Fisher's z

Probability density function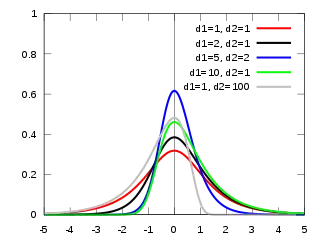
Parameters	${\displaystyle d_{1}>0,\ d_{2}>0}$ deg. of freedom
Support	${\displaystyle x\in (-\infty$ ;+\infty )\!}
PDF	${\displaystyle {\frac {2d_{1}^{d_{1}/2}d_{2}^{d_{2}/2}}{B(d_{1}/2,d_{2}/2)}}{\frac {e^{d_{1}x}}{\left(d_{1}e^{2x}+d_{2}\right)^{\left(d_{1}+d_{2}\right)/2}}}\!}$
Mode	${\displaystyle 0}$

Ronald Fisher

It was first described by Ronald Fisher in a paper delivered at the International Mathematical Congress of 1924 in Toronto.[1] Nowadays one usually uses the F-distribution instead.

The probability density function and cumulative distribution function can be found by using the F-distribution at the value of ${\displaystyle x'=e^{2x}\,}$. However, the mean and variance do not follow the same transformation.

The probability density function is[2][3]

${\displaystyle f(x;d_{1},d_{2})={\frac {2d_{1}^{d_{1}/2}d_{2}^{d_{2}/2}}{B(d_{1}/2,d_{2}/2)}}{\frac {e^{d_{1}x}}{\left(d_{1}e^{2x}+d_{2}\right)^{(d_{1}+d_{2})/2}}},}$

where B is the beta function.

When the degrees of freedom becomes large (${\displaystyle d_{1},d_{2}\rightarrow \infty }$) the distribution approaches normality with mean[2]

${\displaystyle {\bar {x}}={\frac {1}{2}}\left({\frac {1}{d_{2}}}-{\frac {1}{d_{1}}}\right)}$

and variance

${\displaystyle \sigma _{x}^{2}={\frac {1}{2}}\left({\frac {1}{d_{1}}}+{\frac {1}{d_{2}}}\right).}$

Related distribution

• If ${\displaystyle X\sim \operatorname {FisherZ} (n,m)}$ then ${\displaystyle e^{2X}\sim \operatorname {F} (n,m)\,}$ (F-distribution)
• If ${\displaystyle X\sim \operatorname {F} (n,m)}$ then ${\displaystyle {\tfrac {\log X}{2}}\sim \operatorname {FisherZ} (n,m)}$

References

1. Fisher, R. A. (1924). "On a Distribution Yielding the Error Functions of Several Well Known Statistics" (PDF). Proceedings of the International Congress of Mathematics, Toronto. 2: 805–813. Archived from the original (PDF) on April 12, 2011.
2. Leo A. Aroian (December 1941). "A study of R. A. Fisher's z distribution and the related F distribution". The Annals of Mathematical Statistics. 12 (4): 429–448. doi:10.1214/aoms/1177731681. JSTOR 2235955.
3. Charles Ernest Weatherburn (1961). A first course in mathematical statistics.

External links

• MathWorld entry