F-distribution

In probability theory and statistics, the F-distribution, also known as Snedecor's F distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA), e.g., F-test.[2][3][4][5]

Fisher–Snedecor

Probability density function
Cumulative distribution function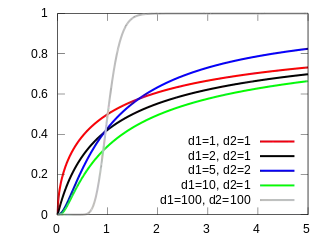
Parameters	d1, d2 > 0 deg. of freedom
Support	${\displaystyle x\in (0,+\infty )\;}$ if ${\displaystyle d_{1}=1}$, otherwise ${\displaystyle x\in [0,+\infty )\;}$
PDF	${\displaystyle {\frac {\sqrt {\frac {(d_{1}x)^{d_{1}}d_{2}^{d_{2}}}{(d_{1}x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\!}$
CDF	${\displaystyle I_{\frac {d_{1}x}{d_{1}x+d_{2}}}\left({\tfrac {d_{1}}{2}},{\tfrac {d_{2}}{2}}\right)}$
Mean	${\displaystyle {\frac {d_{2}}{d_{2}-2}}\!}$ for d2 > 2
Mode	${\displaystyle {\frac {d_{1}-2}{d_{1}}}\;{\frac {d_{2}}{d_{2}+2}}}$ for d1 > 2
Variance	${\displaystyle {\frac {2\,d_{2}^{2}\,(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}\!}$ for d2 > 4
Skewness	${\displaystyle {\frac {(2d_{1}+d_{2}-2){\sqrt {8(d_{2}-4)}}}{(d_{2}-6){\sqrt {d_{1}(d_{1}+d_{2}-2)}}}}\!}$ for d2 > 6
Ex. kurtosis	see text
Entropy	${\displaystyle \ln \Gamma \left({\tfrac {d_{1}}{2}}\right)+\ln \Gamma \left({\tfrac {d_{2}}{2}}\right)-\ln \Gamma \left({\tfrac {d_{1}+d_{2}}{2}}\right)+\!}$ ${\displaystyle \left(1-{\tfrac {d_{1}}{2}}\right)\psi \left(1+{\tfrac {d_{1}}{2}}\right)-\left(1+{\tfrac {d_{2}}{2}}\right)\psi \left(1+{\tfrac {d_{2}}{2}}\right)\!}$ ${\displaystyle +\left({\tfrac {d_{1}+d_{2}}{2}}\right)\psi \left({\tfrac {d_{1}+d_{2}}{2}}\right)+\ln {\frac {d_{1}}{d_{2}}}\!}$[1]
MGF	does not exist, raw moments defined in text and in [2][3]
CF	see text

Definition

If a random variable X has an F-distribution with parameters d₁ and d₂, we write X ~ F(d₁, d₂). Then the probability density function (pdf) for X is given by

${\displaystyle {\begin{aligned}f(x;d_{1},d_{2})&={\frac {\sqrt {\frac {(d_{1}x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\\&={\frac {1}{\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\left({\frac {d_{1}}{d_{2}}}\right)^{\frac {d_{1}}{2}}x^{{\frac {d_{1}}{2}}-1}\left(1+{\frac {d_{1}}{d_{2}}}\,x\right)^{-{\frac {d_{1}+d_{2}}{2}}}\end{aligned}}}$

for real x > 0. Here ${\displaystyle \mathrm {B} }$ is the beta function. In many applications, the parameters d₁ and d₂ are positive integers, but the distribution is well-defined for positive real values of these parameters.

The cumulative distribution function is

${\displaystyle F(x;d_{1},d_{2})=I_{\frac {d_{1}x}{d_{1}x+d_{2}}}\left({\tfrac {d_{1}}{2}},{\tfrac {d_{2}}{2}}\right),}$

where I is the regularized incomplete beta function.

The expectation, variance, and other details about the F(d₁, d₂) are given in the sidebox; for d₂ > 8, the excess kurtosis is

${\displaystyle \gamma _{2}=12{\frac {d_{1}(5d_{2}-22)(d_{1}+d_{2}-2)+(d_{2}-4)(d_{2}-2)^{2}}{d_{1}(d_{2}-6)(d_{2}-8)(d_{1}+d_{2}-2)}}.}$

The k-th moment of an F(d₁, d₂) distribution exists and is finite only when 2k < d₂ and it is equal to [6]

${\displaystyle \mu _{X}(k)=\left({\frac {d_{2}}{d_{1}}}\right)^{k}{\frac {\Gamma \left({\tfrac {d_{1}}{2}}+k\right)}{\Gamma \left({\tfrac {d_{1}}{2}}\right)}}{\frac {\Gamma \left({\tfrac {d_{2}}{2}}-k\right)}{\Gamma \left({\tfrac {d_{2}}{2}}\right)}}}$

The F-distribution is a particular parametrization of the beta prime distribution, which is also called the beta distribution of the second kind.

The characteristic function is listed incorrectly in many standard references (e.g.,[3]). The correct expression [7] is

${\displaystyle \varphi _{d_{1},d_{2}}^{F}(s)={\frac {\Gamma ({\frac {d_{1}+d_{2}}{2}})}{\Gamma ({\tfrac {d_{2}}{2}})}}U\!\left({\frac {d_{1}}{2}},1-{\frac {d_{2}}{2}},-{\frac {d_{2}}{d_{1}}}\imath s\right)}$

where U(a, b, z) is the confluent hypergeometric function of the second kind.

Characterization

A random variate of the F-distribution with parameters ${\displaystyle d_{1}}$ and ${\displaystyle d_{2}}$ arises as the ratio of two appropriately scaled chi-squared variates:[8]

${\displaystyle X={\frac {U_{1}/d_{1}}{U_{2}/d_{2}}}}$

where

• ${\displaystyle U_{1}}$ and ${\displaystyle U_{2}}$ have chi-squared distributions with ${\displaystyle d_{1}}$ and ${\displaystyle d_{2}}$ degrees of freedom respectively, and
• ${\displaystyle U_{1}}$ and ${\displaystyle U_{2}}$ are independent.

In instances where the F-distribution is used, for example in the analysis of variance, independence of ${\displaystyle U_{1}}$ and ${\displaystyle U_{2}}$ might be demonstrated by applying Cochran's theorem.

Equivalently, the random variable of the F-distribution may also be written

${\displaystyle X={\frac {s_{1}^{2}}{\sigma _{1}^{2}}}\div {\frac {s_{2}^{2}}{\sigma _{2}^{2}}},}$

where ${\displaystyle s_{1}^{2}={\frac {S_{1}^{2}}{d_{1}}}}$ and ${\displaystyle s_{2}^{2}={\frac {S_{2}^{2}}{d_{2}}}}$, ${\displaystyle S_{1}^{2}}$ is the sum of squares of ${\displaystyle d_{1}}$ random variables from normal distribution ${\displaystyle N(0,\sigma _{1}^{2})}$ and ${\displaystyle S_{2}^{2}}$ is the sum of squares of ${\displaystyle d_{2}}$ random variables from normal distribution ${\displaystyle N(0,\sigma _{2}^{2})}$.

In a frequentist context, a scaled F-distribution therefore gives the probability ${\displaystyle p(s_{1}^{2}/s_{2}^{2}\mid \sigma _{1}^{2},\sigma _{2}^{2})}$, with the F-distribution itself, without any scaling, applying where ${\displaystyle \sigma _{1}^{2}}$ is being taken equal to ${\displaystyle \sigma _{2}^{2}}$. This is the context in which the F-distribution most generally appears in F-tests: where the null hypothesis is that two independent normal variances are equal, and the observed sums of some appropriately selected squares are then examined to see whether their ratio is significantly incompatible with this null hypothesis.

The quantity ${\displaystyle X}$ has the same distribution in Bayesian statistics, if an uninformative rescaling-invariant Jeffreys prior is taken for the prior probabilities of ${\displaystyle \sigma _{1}^{2}}$ and ${\displaystyle \sigma _{2}^{2}}$.[9] In this context, a scaled F-distribution thus gives the posterior probability ${\displaystyle p(\sigma _{2}^{2}/\sigma _{1}^{2}\mid s_{1}^{2},s_{2}^{2})}$, where the observed sums ${\displaystyle s_{1}^{2}}$ and ${\displaystyle s_{2}^{2}}$ are now taken as known.

Properties and related distributions

• If ${\displaystyle X\sim \chi _{d_{1}}^{2}}$ and ${\displaystyle Y\sim \chi _{d_{2}}^{2}}$ are independent, then ${\displaystyle {\frac {X/d_{1}}{Y/d_{2}}}\sim \mathrm {F} (d_{1},d_{2})}$
• If ${\displaystyle X_{k}\sim \Gamma (\alpha _{k},\beta _{k})\,}$ are independent, then ${\displaystyle {\frac {\alpha _{2}\beta _{1}X_{1}}{\alpha _{1}\beta _{2}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})}$
• If ${\displaystyle X\sim \operatorname {Beta} (d_{1}/2,d_{2}/2)}$ (Beta distribution) then ${\displaystyle {\frac {d_{2}X}{d_{1}(1-X)}}\sim \operatorname {F} (d_{1},d_{2})}$
• Equivalently, if ${\displaystyle X\sim F(d_{1},d_{2})}$, then ${\displaystyle {\frac {d_{1}X/d_{2}}{1+d_{1}X/d_{2}}}\sim \operatorname {Beta} (d_{1}/2,d_{2}/2)}$.
• If ${\displaystyle X\sim F(d_{1},d_{2})}$, then ${\displaystyle {\frac {d_{1}}{d_{2}}}X}$ has a beta prime distribution: ${\displaystyle {\frac {d_{1}}{d_{2}}}X\sim \operatorname {\beta ^{\prime }} ({\tfrac {d_{1}}{2}},{\tfrac {d_{2}}{2}})}$.
• If ${\displaystyle X\sim F(d_{1},d_{2})}$ then ${\displaystyle Y=\lim _{d_{2}\to \infty }d_{1}X}$ has the chi-squared distribution ${\displaystyle \chi _{d_{1}}^{2}}$
• ${\displaystyle F(d_{1},d_{2})}$ is equivalent to the scaled Hotelling's T-squared distribution ${\displaystyle {\frac {d_{2}}{d_{1}(d_{1}+d_{2}-1)}}\operatorname {T} ^{2}(d_{1},d_{1}+d_{2}-1)}$.
• If ${\displaystyle X\sim F(d_{1},d_{2})}$ then ${\displaystyle X^{-1}\sim F(d_{2},d_{1})}$.
• If ${\displaystyle X\sim t_{(n)}}$ — Student's t-distribution — then:

${\displaystyle X^{2}\sim \operatorname {F} (1,n)}$

${\displaystyle X^{-2}\sim \operatorname {F} (n,1)}$

• F-distribution is a special case of type 6 Pearson distribution
• If ${\displaystyle X}$ and ${\displaystyle Y}$ are independent, with ${\displaystyle X,Y\sim }$ Laplace(μ, b) then

${\displaystyle {\frac {|X-\mu |}{|Y-\mu |}}\sim \operatorname {F} (2,2)}$

• If ${\displaystyle X\sim F(n,m)}$ then ${\displaystyle {\tfrac {\log {X}}{2}}\sim \operatorname {FisherZ} (n,m)}$ (Fisher's z-distribution)
• The noncentral F-distribution simplifies to the F-distribution if ${\displaystyle \lambda =0}$.
• The doubly noncentral F-distribution simplifies to the F-distribution if ${\displaystyle \lambda _{1}=\lambda _{2}=0}$
• If ${\displaystyle \operatorname {Q} _{X}(p)}$ is the quantile p for ${\displaystyle X\sim F(d_{1},d_{2})}$ and ${\displaystyle \operatorname {Q} _{Y}(1-p)}$ is the quantile ${\displaystyle 1-p}$ for ${\displaystyle Y\sim F(d_{2},d_{1})}$, then

${\displaystyle \operatorname {Q} _{X}(p)={\frac {1}{\operatorname {Q} _{Y}(1-p)}}.}$

• F-distribution is an instance of ratio distributions

See also

• Beta prime distribution
• Chi-square distribution
• Chow test
• Gamma distribution
• Hotelling's T-squared distribution
• Wilks' lambda distribution
• Wishart distribution

References

1. Lazo, A.V.; Rathie, P. (1978). "On the entropy of continuous probability distributions". IEEE Transactions on Information Theory. IEEE. 24 (1): 120–122. doi:10.1109/tit.1978.1055832.
2. Johnson, Norman Lloyd; Samuel Kotz; N. Balakrishnan (1995). Continuous Univariate Distributions, Volume 2 (Second Edition, Section 27). Wiley. ISBN 0-471-58494-0.
3. Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 26". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 946. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
4. NIST (2006). Engineering Statistics Handbook – F Distribution
5. Mood, Alexander; Franklin A. Graybill; Duane C. Boes (1974). Introduction to the Theory of Statistics (Third ed.). McGraw-Hill. pp. 246–249. ISBN 0-07-042864-6.
6. Taboga, Marco. "The F distribution".
7. Phillips, P. C. B. (1982) "The true characteristic function of the F distribution," Biometrika, 69: 261–264 JSTOR 2335882
8. M.H. DeGroot (1986), Probability and Statistics (2nd Ed), Addison-Wesley. ISBN 0-201-11366-X, p. 500
9. G. E. P. Box and G. C. Tiao (1973), Bayesian Inference in Statistical Analysis, Addison-Wesley. p. 110

External links

• Table of critical values of the F-distribution
• Earliest Uses of Some of the Words of Mathematics: entry on F-distribution contains a brief history
• Free calculator for F-testing