Trigonometric constants expressed in real radicals

Exact algebraic expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification.

The primary solution angles in the form (cos,sin) on the unit circle are at multiples of 30 and 45 degrees.

All trigonometric numbers – sines or cosines of rational multiples of 360° – are algebraic numbers (solutions of polynomial equations with integer coefficients); moreover they may be expressed in terms of radicals of complex numbers; but not all of these are expressible in terms of real radicals. When they are, they are expressible more specifically in terms of square roots.

All values of the sines, cosines, and tangents of angles at 3° increments are expressible in terms of square roots, using identities – the half-angle identity, the double-angle identity, and the angle addition/subtraction identity – and using values for 0°, 30°, 36°, and 45°. For an angle of an integer number of degrees that is not a multiple of 3° (π/60 radians), the values of sine, cosine, and tangent cannot be expressed in terms of real radicals.

According to Niven's theorem, the only rational values of the sine function for which the argument is a rational number of degrees are 0, 1/2,  1, −1/2, and −1.

According to Baker's theorem, if the value of a sine, a cosine or a tangent is algebraic, then the angle is either a rational number of degrees or a transcendental number of degrees. That is, if the angle is an algebraic, but non-rational, number of degrees, the trigonometric functions all have transcendental values.

Scope of this article

The list in this article is incomplete in several senses. First, the trigonometric functions of all angles that are integer multiples of those given can also be expressed in radicals, but some are omitted here.

Second, it is always possible to apply the half-angle formula to find an expression in radicals for a trigonometric function of one-half of any angle on the list, then half of that angle, etc.

Third, expressions in real radicals exist for a trigonometric function of a rational multiple of π if and only if the denominator of the fully reduced rational multiple is a power of 2 by itself or the product of a power of 2 with the product of distinct Fermat primes, of which the known ones are 3, 5, 17, 257, and 65537.

Fourth, this article only deals with trigonometric function values when the expression in radicals is in real radicals – roots of real numbers. Many other trigonometric function values are expressible in, for example, cube roots of complex numbers that cannot be rewritten in terms of roots of real numbers. For example, the trigonometric function values of any angle that is one-third of an angle θ considered in this article can be expressed in cube roots and square roots by using the cubic equation formula to solve

${\displaystyle 4\cos ^{3}{\frac {\theta }{3}}-3\cos {\frac {\theta }{3}}=\cos \theta ,}$

but in general the solution for the cosine of the one-third angle involves the cube root of a complex number (giving casus irreducibilis).

In practice, all values of sines, cosines, and tangents not found in this article are approximated using the techniques described at Trigonometric tables.

Some angles

Exact trigonometric table for multiples of 3 degrees.

Values outside the [0°, 45°] angle range are trivially derived from the following values, using circle axis reflection symmetry. (See List of trigonometric identities.)

In the entries below, when a certain number of degrees is related to a regular polygon, the relation is that the number of degrees in each angle of the polygon is (n – 2) times the indicated number of degrees (where n is the number of sides). This is because the sum of the angles of any n-gon is 180° × (n – 2) and so the measure of each angle of any regular n-gon is 180° × (n – 2) ÷ n. Thus for example the entry "45°: square" means that, with n = 4, 180° ÷ n = 45°, and the number of degrees in each angle of a square is (n – 2) × 45° = 90°.

0°: fundamental

${\displaystyle \sin 0=0\,}$

${\displaystyle \cos 0=1\,}$

${\displaystyle \tan 0=0\,}$

${\displaystyle \cot 0{\text{ is undefined}}\,}$

1.5°: regular hecatonicosagon (120-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{120}}\right)=\sin \left(1.5^{\circ }\right)={\frac {\left({\sqrt {2+{\sqrt {2}}}}\right)\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)-\left({\sqrt {2-{\sqrt {2}}}}\right)\left({\sqrt {30-6{\sqrt {5}}}}+{\sqrt {5}}+1\right)}{16}}}$

${\displaystyle \cos \left({\frac {\pi }{120}}\right)=\cos \left(1.5^{\circ }\right)={\frac {\left({\sqrt {2+{\sqrt {2}}}}\right)\left({\sqrt {30-6{\sqrt {5}}}}+{\sqrt {5}}+1\right)+\left({\sqrt {2-{\sqrt {2}}}}\right)\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)}{16}}}$

1.875°: regular enneacontahexagon (96-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{96}}\right)=\sin \left(1.875^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{96}}\right)=\cos \left(1.875^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}}}$

2.25°: regular octacontagon (80-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{80}}\right)=\sin \left(2.25^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{80}}\right)=\cos \left(2.25^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}}}}}$

2.8125°: regular hexacontatetragon (64-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{64}}\right)=\sin \left(2.8125^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{64}}\right)=\cos \left(2.8125^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}}}$

3°: regular hexacontagon (60-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{60}}\right)=\sin \left(3^{\circ }\right)={\frac {2\left(1-{\sqrt {3}}\right){\sqrt {5+{\sqrt {5}}}}+\left({\sqrt {10}}-{\sqrt {2}}\right)\left({\sqrt {3}}+1\right)}{16}}\,}$

${\displaystyle \cos \left({\frac {\pi }{60}}\right)=\cos \left(3^{\circ }\right)={\frac {2\left(1+{\sqrt {3}}\right){\sqrt {5+{\sqrt {5}}}}+\left({\sqrt {10}}-{\sqrt {2}}\right)\left({\sqrt {3}}-1\right)}{16}}\,}$

${\displaystyle \tan \left({\frac {\pi }{60}}\right)=\tan \left(3^{\circ }\right)={\frac {\left[\left(2-{\sqrt {3}}\right)\left(3+{\sqrt {5}}\right)-2\right]\left[2-{\sqrt {10-2{\sqrt {5}}}}\right]}{4}}\,}$

${\displaystyle \cot \left({\frac {\pi }{60}}\right)=\cot \left(3^{\circ }\right)={\frac {\left[\left(2+{\sqrt {3}}\right)\left(3+{\sqrt {5}}\right)-2\right]\left[2+{\sqrt {10-2{\sqrt {5}}}}\right]}{4}}\,}$

3.75°: regular tetracontaoctagon (48-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{48}}\right)=\sin \left(3.75^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{48}}\right)=\cos \left(3.75^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}$

4.5°: regular tetracontagon (40-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{40}}\right)=\sin \left(4.5^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{40}}\right)=\cos \left(4.5^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}}}$

5.625°: regular triacontadigon (32-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{32}}\right)=\sin \left(5.625^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}$

${\displaystyle \cos \left({\frac {\pi }{32}}\right)=\cos \left(5.625^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}$

6°: regular triacontagon (30-sided polygon)

${\displaystyle \sin {\frac {\pi }{30}}=\sin 6^{\circ }={\frac {{\sqrt {30-{\sqrt {180}}}}-{\sqrt {5}}-1}{8}}\,}$

${\displaystyle \cos {\frac {\pi }{30}}=\cos 6^{\circ }={\frac {{\sqrt {10-{\sqrt {20}}}}+{\sqrt {3}}+{\sqrt {15}}}{8}}\,}$

${\displaystyle \tan {\frac {\pi }{30}}=\tan 6^{\circ }={\frac {{\sqrt {10-{\sqrt {20}}}}+{\sqrt {3}}-{\sqrt {15}}}{2}}\,}$

${\displaystyle \cot {\frac {\pi }{30}}=\cot 6^{\circ }={\frac {{\sqrt {27}}+{\sqrt {15}}+{\sqrt {50+{\sqrt {2420}}}}}{2}}\,}$

7.5°: regular icositetragon (24-sided polygon)

${\displaystyle \sin \left({\frac {\pi }{24}}\right)=\sin \left(7.5^{\circ }\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {3}}}}}}={\frac {1}{4}}{\sqrt {8-2{\sqrt {6}}-2{\sqrt {2}}}}}$

${\displaystyle \cos \left({\frac {\pi }{24}}\right)=\cos \left(7.5^{\circ }\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}={\frac {1}{4}}{\sqrt {8+2{\sqrt {6}}+2{\sqrt {2}}}}}$

${\displaystyle \tan \left({\frac {\pi }{24}}\right)=\tan \left(7.5^{\circ }\right)={\sqrt {6}}-{\sqrt {3}}+{\sqrt {2}}-2\ =\left({\sqrt {2}}-1\right)\left({\sqrt {3}}-{\sqrt {2}}\right)}$

${\displaystyle \cot \left({\frac {\pi }{24}}\right)=\cot \left(7.5^{\circ }\right)={\sqrt {6}}+{\sqrt {3}}+{\sqrt {2}}+2\ =\left({\sqrt {2}}+1\right)\left({\sqrt {3}}+{\sqrt {2}}\right)}$

9°: regular icosagon (20-sided polygon)

${\displaystyle \sin {\frac {\pi }{20}}=\sin 9^{\circ }={\frac {1}{2}}{\sqrt {2-{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}$

${\displaystyle \cos {\frac {\pi }{20}}=\cos 9^{\circ }={\frac {1}{2}}{\sqrt {2+{\sqrt {\frac {5+{\sqrt {5}}}{2}}}}}}$

${\displaystyle \tan {\frac {\pi }{20}}=\tan 9^{\circ }={\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}\,}$

${\displaystyle \cot {\frac {\pi }{20}}=\cot 9^{\circ }={\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}\,}$

11.25°: regular hexadecagon (16-sided polygon)

${\displaystyle \sin {\frac {\pi }{16}}=\sin 11.25^{\circ }={\frac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}$

${\displaystyle \cos {\frac {\pi }{16}}=\cos 11.25^{\circ }={\frac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}$

${\displaystyle \tan {\frac {\pi }{16}}=\tan 11.25^{\circ }={\sqrt {4+2{\sqrt {2}}}}-{\sqrt {2}}-1}$

${\displaystyle \cot {\frac {\pi }{16}}=\cot 11.25^{\circ }={\sqrt {4+2{\sqrt {2}}}}+{\sqrt {2}}+1}$

12°: regular pentadecagon (15-sided polygon)

${\displaystyle \sin {\frac {\pi }{15}}=\sin 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {2\left(5+{\sqrt {5}}\right)}}+{\sqrt {3}}-{\sqrt {15}}\right]\,}$

${\displaystyle \cos {\frac {\pi }{15}}=\cos 12^{\circ }={\tfrac {1}{8}}\left[{\sqrt {6\left(5+{\sqrt {5}}\right)}}+{\sqrt {5}}-1\right]\,}$

${\displaystyle \tan {\frac {\pi }{15}}=\tan 12^{\circ }={\tfrac {1}{2}}\left[3{\sqrt {3}}-{\sqrt {15}}-{\sqrt {2\left(25-11{\sqrt {5}}\right)}}\,\right]\,}$

${\displaystyle \cot {\frac {\pi }{15}}=\cot 12^{\circ }={\tfrac {1}{2}}\left[{\sqrt {15}}+{\sqrt {3}}+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,\right]\,}$

15°: regular dodecagon (12-sided polygon)

${\displaystyle \sin {\frac {\pi }{12}}=\sin 15^{\circ }={\frac {1}{4}}\left({\sqrt {6}}-{\sqrt {2}}\right)={\frac {1}{2}}{\sqrt {2-{\sqrt {3}}}}}$

${\displaystyle \cos {\frac {\pi }{12}}=\cos 15^{\circ }={\frac {1}{4}}\left({\sqrt {6}}+{\sqrt {2}}\right)={\frac {1}{2}}{\sqrt {2+{\sqrt {3}}}}}$

${\displaystyle \tan {\frac {\pi }{12}}=\tan 15^{\circ }=2-{\sqrt {3}}\,}$

${\displaystyle \cot {\frac {\pi }{12}}=\cot 15^{\circ }=2+{\sqrt {3}}\,}$

18°: regular decagon (10-sided polygon)[1]

${\displaystyle \sin {\frac {\pi }{10}}=\sin 18^{\circ }={\tfrac {1}{4}}\left({\sqrt {5}}-1\right)={\frac {1}{1+{\sqrt {5}}}}\,}$

${\displaystyle \cos {\frac {\pi }{10}}=\cos 18^{\circ }={\tfrac {1}{4}}{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,}$

${\displaystyle \tan {\frac {\pi }{10}}=\tan 18^{\circ }={\tfrac {1}{5}}{\sqrt {5\left(5-2{\sqrt {5}}\right)}}\,}$

${\displaystyle \cot {\frac {\pi }{10}}=\cot 18^{\circ }={\sqrt {5+2{\sqrt {5}}}}\,}$

21°: sum 9° + 12°

${\displaystyle \sin {\frac {7\pi }{60}}=\sin 21^{\circ }={\frac {1}{16}}\left(2\left({\sqrt {3}}+1\right){\sqrt {5-{\sqrt {5}}}}-\left({\sqrt {6}}-{\sqrt {2}}\right)\left(1+{\sqrt {5}}\right)\right)\,}$

${\displaystyle \cos {\frac {7\pi }{60}}=\cos 21^{\circ }={\frac {1}{16}}\left(2\left({\sqrt {3}}-1\right){\sqrt {5-{\sqrt {5}}}}+\left({\sqrt {6}}+{\sqrt {2}}\right)\left(1+{\sqrt {5}}\right)\right)\,}$

${\displaystyle \tan {\frac {7\pi }{60}}=\tan 21^{\circ }={\frac {1}{4}}\left(2-\left(2+{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)\right)\left(2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right)\,}$

${\displaystyle \cot {\frac {7\pi }{60}}=\cot 21^{\circ }={\frac {1}{4}}\left(2-\left(2-{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)\right)\left(2+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\right)\,}$

22.5°: regular octagon

${\displaystyle \sin {\frac {\pi }{8}}=\sin 22.5^{\circ }={\frac {1}{2}}{\sqrt {2-{\sqrt {2}}}},}$

${\displaystyle \cos {\frac {\pi }{8}}=\cos 22.5^{\circ }={\frac {1}{2}}{\sqrt {2+{\sqrt {2}}}}\,}$

${\displaystyle \tan {\frac {\pi }{8}}=\tan 22.5^{\circ }={\sqrt {2}}-1\,}$

${\displaystyle \cot {\frac {\pi }{8}}=\cot 22.5^{\circ }={\sqrt {2}}+1=\delta _{S}\,}$, the silver ratio

24°: sum 12° + 12°

${\displaystyle \sin {\frac {2\pi }{15}}=\sin 24^{\circ }={\tfrac {1}{8}}\left[{\sqrt {15}}+{\sqrt {3}}-{\sqrt {2\left(5-{\sqrt {5}}\right)}}\right]\,}$

${\displaystyle \cos {\frac {2\pi }{15}}=\cos 24^{\circ }={\tfrac {1}{8}}\left({\sqrt {6\left(5-{\sqrt {5}}\right)}}+{\sqrt {5}}+1\right)\,}$

${\displaystyle \tan {\frac {2\pi }{15}}=\tan 24^{\circ }={\tfrac {1}{2}}\left[{\sqrt {50+22{\sqrt {5}}}}-3{\sqrt {3}}-{\sqrt {15}}\right]\,}$

${\displaystyle \cot {\frac {2\pi }{15}}=\cot 24^{\circ }={\tfrac {1}{2}}\left[{\sqrt {15}}-{\sqrt {3}}+{\sqrt {2\left(5-{\sqrt {5}}\right)}}\right]\,}$

27°: sum 12° + 15°

${\displaystyle \sin {\frac {3\pi }{20}}=\sin 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}-{\sqrt {2}}\;\left({\sqrt {5}}-1\right)\right]\,}$

${\displaystyle \cos {\frac {3\pi }{20}}=\cos 27^{\circ }={\tfrac {1}{8}}\left[2{\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}\;\left({\sqrt {5}}-1\right)\right]\,}$

${\displaystyle \tan {\frac {3\pi }{20}}=\tan 27^{\circ }={\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}\,}$

${\displaystyle \cot {\frac {3\pi }{20}}=\cot 27^{\circ }={\sqrt {5}}-1+{\sqrt {5-2{\sqrt {5}}}}\,}$

30°: regular hexagon

${\displaystyle \sin {\frac {\pi }{6}}=\sin 30^{\circ }={\frac {1}{2}}\,}$

${\displaystyle \cos {\frac {\pi }{6}}=\cos 30^{\circ }={\frac {\sqrt {3}}{2}}\,}$

${\displaystyle \tan {\frac {\pi }{6}}=\tan 30^{\circ }={\frac {\sqrt {3}}{3}}={\frac {1}{\sqrt {3}}}\,}$

${\displaystyle \cot {\frac {\pi }{6}}=\cot 30^{\circ }={\sqrt {3}}\,}$

33°: sum 15° + 18°

${\displaystyle \sin {\frac {11\pi }{60}}=\sin 33^{\circ }={\tfrac {1}{16}}\left[2\left({\sqrt {3}}-1\right){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}\left(1+{\sqrt {3}}\right)\left({\sqrt {5}}-1\right)\right]\,}$

${\displaystyle \cos {\frac {11\pi }{60}}=\cos 33^{\circ }={\tfrac {1}{16}}\left[2\left({\sqrt {3}}+1\right){\sqrt {5+{\sqrt {5}}}}+{\sqrt {2}}\left(1-{\sqrt {3}}\right)\left({\sqrt {5}}-1\right)\right]\,}$

${\displaystyle \tan {\frac {11\pi }{60}}=\tan 33^{\circ }={\tfrac {1}{4}}\left[2-\left(2-{\sqrt {3}}\right)\left(3+{\sqrt {5}}\right)\right]\left[2+{\sqrt {2\left(5-{\sqrt {5}}\right)}}\,\right]\,}$

${\displaystyle \cot {\frac {11\pi }{60}}=\cot 33^{\circ }={\tfrac {1}{4}}\left[2-\left(2+{\sqrt {3}}\right)\left(3+{\sqrt {5}}\right)\right]\left[2-{\sqrt {2\left(5-{\sqrt {5}}\right)}}\,\right]\,}$

36°: regular pentagon

[1]

${\displaystyle \sin {\frac {\pi }{5}}=\sin 36^{\circ }={\frac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}}$

${\displaystyle \cos {\frac {\pi }{5}}=\cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}}={\frac {\varphi }{2}},}$ where φ is the golden ratio;

${\displaystyle \tan {\frac {\pi }{5}}=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}\,}$

${\displaystyle \cot {\frac {\pi }{5}}=\cot 36^{\circ }={\frac {1}{5}}{\sqrt {25+10{\sqrt {5}}}}}$

39°: sum 18° + 21°

${\displaystyle \sin {\frac {13\pi }{60}}=\sin 39^{\circ }={\tfrac {1}{16}}\left[2\left(1-{\sqrt {3}}\right){\sqrt {5-{\sqrt {5}}}}+{\sqrt {2}}\left({\sqrt {3}}+1\right)\left({\sqrt {5}}+1\right)\right]\,}$

${\displaystyle \cos {\frac {13\pi }{60}}=\cos 39^{\circ }={\tfrac {1}{16}}\left[2\left(1+{\sqrt {3}}\right){\sqrt {5-{\sqrt {5}}}}+{\sqrt {2}}\left({\sqrt {3}}-1\right)\left({\sqrt {5}}+1\right)\right]\,}$

${\displaystyle \tan {\frac {13\pi }{60}}=\tan 39^{\circ }={\tfrac {1}{4}}\left[\left(2-{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)-2\right]\left[2-{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,\right]\,}$

${\displaystyle \cot {\frac {13\pi }{60}}=\cot 39^{\circ }={\tfrac {1}{4}}\left[\left(2+{\sqrt {3}}\right)\left(3-{\sqrt {5}}\right)-2\right]\left[2+{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,\right]\,}$

42°: sum 21° + 21°

${\displaystyle \sin {\frac {7\pi }{30}}=\sin 42^{\circ }={\frac {{\sqrt {30+6{\sqrt {5}}}}-{\sqrt {5}}+1}{8}}\,}$

${\displaystyle \cos {\frac {7\pi }{30}}=\cos 42^{\circ }={\frac {{\sqrt {15}}-{\sqrt {3}}+{\sqrt {10+2{\sqrt {5}}}}}{8}}\,}$

${\displaystyle \tan {\frac {7\pi }{30}}=\tan 42^{\circ }={\frac {{\sqrt {15}}+{\sqrt {3}}-{\sqrt {10+2{\sqrt {5}}}}}{2}}\,}$

${\displaystyle \cot {\frac {7\pi }{30}}=\cot 42^{\circ }={\frac {{\sqrt {50-22{\sqrt {5}}}}+3{\sqrt {3}}-{\sqrt {15}}}{2}}\,}$

45°: square

${\displaystyle \sin {\frac {\pi }{4}}=\sin 45^{\circ }={\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}\,}$

${\displaystyle \cos {\frac {\pi }{4}}=\cos 45^{\circ }={\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}\,}$

${\displaystyle \tan {\frac {\pi }{4}}=\tan 45^{\circ }=1\,}$

${\displaystyle \cot {\frac {\pi }{4}}=\cot 45^{\circ }=1\,}$

54°: sum 27° + 27°

${\displaystyle \sin {\frac {3\pi }{10}}=\sin 54^{\circ }={\frac {{\sqrt {5}}+1}{4}}\,\!}$

${\displaystyle \cos {\frac {3\pi }{10}}=\cos 54^{\circ }={\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}$

${\displaystyle \tan {\frac {3\pi }{10}}=\tan 54^{\circ }={\frac {\sqrt {25+10{\sqrt {5}}}}{5}}\,}$

${\displaystyle \cot {\frac {3\pi }{10}}=\cot 54^{\circ }={\sqrt {5-2{\sqrt {5}}}}\,}$

60°: equilateral triangle

${\displaystyle \sin {\frac {\pi }{3}}=\sin 60^{\circ }={\frac {\sqrt {3}}{2}}\,}$

${\displaystyle \cos {\frac {\pi }{3}}=\cos 60^{\circ }={\frac {1}{2}}\,}$

${\displaystyle \tan {\frac {\pi }{3}}=\tan 60^{\circ }={\sqrt {3}}\,}$

${\displaystyle \cot {\frac {\pi }{3}}=\cot 60^{\circ }={\frac {\sqrt {3}}{3}}={\frac {1}{\sqrt {3}}}\,}$

67.5°: sum 7.5° + 60°

${\displaystyle \sin {\frac {3\pi }{8}}=\sin 67.5^{\circ }={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2}}}}\,}$

${\displaystyle \cos {\frac {3\pi }{8}}=\cos 67.5^{\circ }={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2}}}}\,}$

${\displaystyle \tan {\frac {3\pi }{8}}=\tan 67.5^{\circ }={\sqrt {2}}+1\,}$

${\displaystyle \cot {\frac {3\pi }{8}}=\cot 67.5^{\circ }={\sqrt {2}}-1\,}$

72°: sum 36° + 36°

${\displaystyle \sin {\frac {2\pi }{5}}=\sin 72^{\circ }={\tfrac {1}{4}}{\sqrt {2\left(5+{\sqrt {5}}\right)}}\,}$

${\displaystyle \cos {\frac {2\pi }{5}}=\cos 72^{\circ }={\tfrac {1}{4}}\left({\sqrt {5}}-1\right)\,}$

${\displaystyle \tan {\frac {2\pi }{5}}=\tan 72^{\circ }={\sqrt {5+2{\sqrt {5}}}}\,}$

${\displaystyle \cot {\frac {2\pi }{5}}=\cot 72^{\circ }={\tfrac {1}{5}}{\sqrt {5\left(5-2{\sqrt {5}}\right)}}\,}$

75°: sum 30° + 45°

${\displaystyle \sin {\frac {5\pi }{12}}=\sin 75^{\circ }={\tfrac {1}{4}}\left({\sqrt {6}}+{\sqrt {2}}\right)\,}$

${\displaystyle \cos {\frac {5\pi }{12}}=\cos 75^{\circ }={\tfrac {1}{4}}\left({\sqrt {6}}-{\sqrt {2}}\right)\,}$

${\displaystyle \tan {\frac {5\pi }{12}}=\tan 75^{\circ }=2+{\sqrt {3}}\,}$

${\displaystyle \cot {\frac {5\pi }{12}}=\cot 75^{\circ }=2-{\sqrt {3}}\,}$

90°: fundamental

${\displaystyle \sin {\frac {\pi }{2}}=\sin 90^{\circ }=1\,}$

${\displaystyle \cos {\frac {\pi }{2}}=\cos 90^{\circ }=0\,}$

${\displaystyle \tan {\frac {\pi }{2}}=\tan 90^{\circ }{\text{ is undefined}}\,}$

${\displaystyle \cot {\frac {\pi }{2}}=\cot 90^{\circ }=0\,}$

List of trigonometric constants of 2π/n

For cube roots of non-real numbers that appear in this table, one has to take the principal value, that is the cube root with the largest real part; this largest real part is always positive. Therefore, the sums of cube roots that appear in the table are all positive real numbers.

${\displaystyle {\begin{array}{r|l|l|l}n&\sin \left({\frac {2\pi }{n}}\right)&\cos \left({\frac {2\pi }{n}}\right)&\tan \left({\frac {2\pi }{n}}\right)\\\hline 1&0&1&0\\\hline 2&0&-1&0\\\hline 3&{\frac {1}{2}}{\sqrt {3}}&-{\frac {1}{2}}&-{\sqrt {3}}\\\hline 4&1&0&\pm \infty \\\hline 5&{\frac {1}{4}}\left({\sqrt {10+2{\sqrt {5}}}}\right)&{\frac {1}{4}}\left({\sqrt {5}}-1\right)&{\sqrt {5+2{\sqrt {5}}}}\\\hline 6&{\frac {1}{2}}{\sqrt {3}}&{\frac {1}{2}}&{\sqrt {3}}\\\hline 7&&{\frac {1}{6}}\left(-1+{\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}+{\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}\right)&\\\hline 8&{\frac {1}{2}}{\sqrt {2}}&{\frac {1}{2}}{\sqrt {2}}&1\\\hline 9&{\frac {i}{2}}\left({\sqrt[{3}]{\frac {-1-{\sqrt {-3}}}{2}}}-{\sqrt[{3}]{\frac {-1+{\sqrt {-3}}}{2}}}\right)&{\frac {1}{2}}\left({\sqrt[{3}]{\frac {-1+{\sqrt {-3}}}{2}}}+{\sqrt[{3}]{\frac {-1-{\sqrt {-3}}}{2}}}\right)&\\\hline 10&{\frac {1}{4}}\left({\sqrt {10-2{\sqrt {5}}}}\right)&{\frac {1}{4}}\left({\sqrt {5}}+1\right)&{\sqrt {5-2{\sqrt {5}}}}\\\hline 11&&&\\\hline 12&{\frac {1}{2}}&{\frac {1}{2}}{\sqrt {3}}&{\frac {1}{3}}{\sqrt {3}}\\\hline 13&&{\frac {1}{12}}\left({\sqrt[{3}]{104-20{\sqrt {13}}+12{\sqrt {-39}}}}+{\sqrt[{3}]{104-20{\sqrt {13}}-12{\sqrt {-39}}}}+{\sqrt {13}}-1\right)&\\\hline 14&{\frac {1}{24}}{\sqrt {3\left(112-{\sqrt[{3}]{14336+{\sqrt {-5549064192}}}}-{\sqrt[{3}]{14336-{\sqrt {-5549064192}}}}\right)}}&{\frac {1}{24}}{\sqrt {3\left(80+{\sqrt[{3}]{14336+{\sqrt {-5549064192}}}}+{\sqrt[{3}]{14336-{\sqrt {-5549064192}}}}\right)}}&{\sqrt {\frac {112-{\sqrt[{3}]{14336+{\sqrt {-5549064192}}}}-{\sqrt[{3}]{14336-{\sqrt {-5549064192}}}}}{80+{\sqrt[{3}]{14336+{\sqrt {-5549064192}}}}+{\sqrt[{3}]{14336-{\sqrt {-5549064192}}}}}}}\\\hline 15&{\frac {1}{8}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)&{\frac {1}{8}}\left(1+{\sqrt {5}}+{\sqrt {30-6{\sqrt {5}}}}\right)&{\frac {1}{2}}\left(-3{\sqrt {3}}-{\sqrt {15}}+{\sqrt {50+22{\sqrt {5}}}}\right)\\\hline 16&{\frac {1}{2}}\left({\sqrt {2-{\sqrt {2}}}}\right)&{\frac {1}{2}}\left({\sqrt {2+{\sqrt {2}}}}\right)&{\sqrt {2}}-1\\\hline 17&{\frac {1}{4}}{\sqrt {8-{\sqrt {2\left(15+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {17+3{\sqrt {17}}-{\sqrt {170+38{\sqrt {17}}}}}}\right)}}}}&{\frac {1}{16}}\left(-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+2{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}\right)&\\\hline 18&{\frac {i}{4}}\left({\sqrt[{3}]{4-4{\sqrt {-3}}}}-{\sqrt[{3}]{4+4{\sqrt {-3}}}}\right)&{\frac {1}{4}}\left({\sqrt[{3}]{4+4{\sqrt {-3}}}}+{\sqrt[{3}]{4-4{\sqrt {-3}}}}\right)&\\\hline 20&{\frac {1}{4}}\left({\sqrt {5}}-1\right)&{\frac {1}{4}}\left({\sqrt {10+2{\sqrt {5}}}}\right)&{\frac {1}{5}}\left({\sqrt {25-10{\sqrt {5}}}}\right)\\\hline 24&{\frac {1}{4}}\left({\sqrt {6}}-{\sqrt {2}}\right)&{\frac {1}{4}}\left({\sqrt {6}}+{\sqrt {2}}\right)&2-{\sqrt {3}}\\\hline 25&&{\frac {1}{2}}\left({\sqrt[{5}]{\frac {-1+{\sqrt {5}}+{\sqrt {-10-2{\sqrt {5}}}}}{4}}}+{\sqrt[{5}]{\frac {-1+{\sqrt {5}}-{\sqrt {-10-2{\sqrt {5}}}}}{4}}}\right)&\\\end{array}}}$

Notes

Uses for constants

As an example of the use of these constants, consider the volume of a regular dodecahedron, where a is the length of an edge:

${\displaystyle V={\frac {5a^{3}\cos 36^{\circ }}{\tan ^{2}{36^{\circ }}}}.}$

Using

${\displaystyle \cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}},\,}$

${\displaystyle \tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}},\,}$

this can be simplified to:

${\displaystyle V={\frac {a^{3}\left(15+7{\sqrt {5}}\right)}{4}}.\,}$

Derivation triangles

Regular polygon (n-sided) and its fundamental right triangle. Angles: a = 180°/n and b =90(1 − 2/n)°

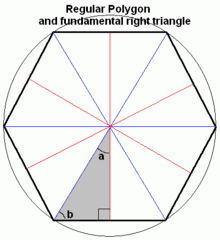
The derivation of sine, cosine, and tangent constants into radial forms is based upon the constructibility of right triangles.

Here right triangles made from symmetry sections of regular polygons are used to calculate fundamental trigonometric ratios. Each right triangle represents three points in a regular polygon: a vertex, an edge center containing that vertex, and the polygon center. An n-gon can be divided into 2n right triangles with angles of 180/n, 90 − 180/n, 90 degrees, for n in 3, 4, 5, …

Constructibility of 3, 4, 5, and 15-sided polygons are the basis, and angle bisectors allow multiples of two to also be derived.

• Constructible
  • 3 × 2ⁿ-sided regular polygons, for n = 0, 1, 2, 3, ...
    • 30°-60°-90° triangle: triangle (3-sided)
    • 60°-30°-90° triangle: hexagon (6-sided)
    • 75°-15°-90° triangle: dodecagon (12-sided)
    • 82.5°-7.5°-90° triangle: icositetragon (24-sided)
    • 86.25°-3.75°-90° triangle: tetracontaoctagon (48-sided)
    • 88.125°-1.875°-90° triangle: enneacontahexagon (96-sided)
    • 89.0625°-0.9375°-90° triangle: 192-gon
    • 89.53125°-0.46875°-90° triangle: 384-gon
    • ...
  • 4 × 2ⁿ-sided
    • 45°-45°-90° triangle: square (4-sided)
    • 67.5°-22.5°-90° triangle: octagon (8-sided)
    • 78.75°-11.25°-90° triangle: hexadecagon (16-sided)
    • 84.375°-5.625°-90° triangle: triacontadigon (32-sided)
    • 87.1875°-2.8125°-90° triangle: hexacontatetragon (64-sided)
    • 88.09375°-1.40625°-90° triangle: 128-gon
    • 89.046875°-0.703125°-90° triangle: 256-gon
    • ...
  • 5 × 2ⁿ-sided
    • 54°-36°-90° triangle: pentagon (5-sided)
    • 72°-18°-90° triangle: decagon (10-sided)
    • 81°-9°-90° triangle: icosagon (20-sided)
    • 85.5°-4.5°-90° triangle: tetracontagon (40-sided)
    • 87.75°-2.25°-90° triangle: octacontagon (80-sided)
    • 88.875°-1.125°-90° triangle: 160-gon
    • 89.4375°-0.5625°-90° triangle: 320-gon
    • ...
  • 15 × 2ⁿ-sided
    • 78°-12°-90° triangle: pentadecagon (15-sided)
    • 84°-6°-90° triangle: triacontagon (30-sided)
    • 87°-3°-90° triangle: hexacontagon (60-sided)
    • 88.5°-1.5°-90° triangle: hecatonicosagon (120-sided)
    • 89.25°-0.75°-90° triangle: 240-gon
  • ...

There are also higher constructible regular polygons: 17, 51, 85, 255, 257, 353, 449, 641, 1409, 2547, ..., 65535, 65537, 69481, 73697, ..., 4294967295.)

• Nonconstructible (with whole or half degree angles) – No finite radical expressions involving real numbers for these triangle edge ratios are possible, therefore its multiples of two are also not possible.
  • 9 × 2ⁿ-sided
    • 70°-20°-90° triangle: enneagon (9-sided)
    • 80°-10°-90° triangle: octadecagon (18-sided)
    • 85°-5°-90° triangle: triacontahexagon (36-sided)
    • 87.5°-2.5°-90° triangle: heptacontadigon (72-sided)
    • ...
  • 45 × 2ⁿ-sided
    • 86°-4°-90° triangle: tetracontapentagon (45-sided)
    • 88°-2°-90° triangle: enneacontagon (90-sided)
    • 89°-1°-90° triangle: 180-gon
    • 89.5°-0.5°-90° triangle: 360-gon
    • ...

Calculated trigonometric values for sine and cosine

The trivial values

In degree format, sin and cos of 0, 30, 45, 60, and 90 can be calculated from their right angled triangles, using the Pythagorean theorem.

In radian format, sin and cos of π / 2ⁿ can be expressed in radical format by recursively applying the following:

${\displaystyle 2\cos \theta ={\sqrt {2+2\cos 2\theta }}={\sqrt {2+{\sqrt {2+2\cos 4\theta }}}}={\sqrt {2+{\sqrt {2+{\sqrt {2+2\cos 8\theta }}}}}}}$ and so on.

${\displaystyle 2\sin \theta ={\sqrt {2-2\cos 2\theta }}={\sqrt {2-{\sqrt {2+2\cos 4\theta }}}}={\sqrt {2-{\sqrt {2+{\sqrt {2+2\cos 8\theta }}}}}}}$ and so on.

For example:

${\displaystyle \cos {\frac {\pi }{2^{1}}}={\frac {0}{2}}}$

${\displaystyle \cos {\frac {\pi }{2^{2}}}={\frac {\sqrt {2+0}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{2^{2}}}={\frac {\sqrt {2-0}}{2}}}$

${\displaystyle \cos {\frac {\pi }{2^{3}}}={\frac {\sqrt {2+{\sqrt {2}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{2^{3}}}={\frac {\sqrt {2-{\sqrt {2}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{2^{4}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{2^{4}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{2^{5}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{2^{5}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{2^{6}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{2^{6}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}}{2}}}$

and so on.

Radical form, sin and cos of π/(3 × 2ⁿ)

${\displaystyle \cos {\frac {2\pi }{3}}={\frac {-1}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{0}}}={\frac {\sqrt {2-1}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{0}}}={\frac {\sqrt {2+1}}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{1}}}={\frac {\sqrt {2+1}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{1}}}={\frac {\sqrt {2-1}}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{2}}}={\frac {\sqrt {2+{\sqrt {3}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{2}}}={\frac {\sqrt {2-{\sqrt {3}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{3}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{3}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {3}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{4}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{4}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{3\times 2^{5}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{3\times 2^{5}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {3}}}}}}}}}}{2}}}$

and so on.

Radical form, sin and cos of π/(5 × 2ⁿ)

${\displaystyle \cos {\frac {2\pi }{5}}={\frac {{\sqrt {5}}-1}{4}}}$

${\displaystyle \cos {\frac {\pi }{5\times 2^{0}}}={\frac {{\sqrt {5}}+1}{4}}}$ ( Therefore ${\displaystyle 2+2\cos {\frac {\pi }{5}}=2+{\sqrt {1.25}}+0.5}$ )

${\displaystyle \cos {\frac {\pi }{5\times 2^{1}}}={\frac {\sqrt {2.5+{\sqrt {1.25}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{5\times 2^{1}}}={\frac {\sqrt {1.5-{\sqrt {1.25}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{5\times 2^{2}}}={\frac {\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{5\times 2^{2}}}={\frac {\sqrt {2-{\sqrt {2.5+{\sqrt {1.25}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{5\times 2^{3}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{5\times 2^{3}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{5\times 2^{4}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{5\times 2^{4}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{5\times 2^{5}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{5\times 2^{5}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2.5+{\sqrt {1.25}}}}}}}}}}}}{2}}}$

and so on.

Radical form, sin and cos of π/(5 × 3 × 2ⁿ)

${\displaystyle \cos {\frac {\pi }{15\times 2^{0}}}={\frac {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}-0.25}{2}}}$

${\displaystyle \cos {\frac {\pi }{15\times 2^{1}}}={\frac {\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{15\times 2^{1}}}={\frac {\sqrt {2.25-{\sqrt {{\sqrt {0.703125}}+1.875}}-{\sqrt {0.3125}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{15\times 2^{2}}}={\frac {\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{15\times 2^{2}}}={\frac {\sqrt {2-{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{15\times 2^{3}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{15\times 2^{3}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{15\times 2^{4}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{15\times 2^{4}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}}}{2}}}$

${\displaystyle \cos {\frac {\pi }{15\times 2^{5}}}={\frac {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{15\times 2^{5}}}={\frac {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {{\sqrt {{\sqrt {0.703125}}+1.875}}+{\sqrt {0.3125}}+1.75}}}}}}}}}}{2}}}$

and so on.

Radical form, sin and cos of π/(17 × 2ⁿ)

If ${\displaystyle M=2(17+{\sqrt {17}})}$ and ${\displaystyle N=2(17-{\sqrt {17}})}$ then

${\displaystyle \cos {\frac {\pi }{17}}={\frac {\sqrt {M-4+2({\sqrt {N}}+{\sqrt {2(2M-N+{\sqrt {17N}}-{\sqrt {N}}-8{\sqrt {M}})}})}}{8}}.}$

Therefore, applying induction:

${\displaystyle \cos {\frac {\pi }{17\times 2^{0}}}={\frac {\sqrt {30+2{\sqrt {17}}+{\sqrt {136-8{\sqrt {17}}}}+{\sqrt {272+48{\sqrt {17}}+8{\sqrt {34-2{\sqrt {17}}}}\times ({\sqrt {17}}-1)-64{\sqrt {34+2{\sqrt {17}}}}}}}}{8}};}$

${\displaystyle \cos {\frac {\pi }{17\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{17\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{17\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{17\times 2^{n}}}}}{2}}.}$

Radical form, sin and cos of π/(257 × 2ⁿ) and π/(65537 × 2ⁿ)

The induction above can be applied in the same way to all the remaining Fermat primes (F₃=2²³+1=2⁸+1=257 and F₄=2²⁴+1=2¹⁶+1=65537), the factors of π whose cos and sin radical expressions are known to exist but are very long to express here.

${\displaystyle \cos {\frac {\pi }{257\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{257\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{257\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{257\times 2^{n}}}}}{2}};}$

${\displaystyle \cos {\frac {\pi }{65537\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{65537\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{65537\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{65537\times 2^{n}}}}}{2}}.}$

Radical form, sin and cos of π/(255 × 2ⁿ), π/(65535 × 2ⁿ) and π/(4294967295 × 2ⁿ)

D = 2³² - 1 = 4,294,967,295 is the largest odd integer denominator for which radical forms for sin(π/D) and cos (π/D) are known to exist.

Using the radical form values from the sections above, and applying cos(A-B) = cosA cosB + sinA sinB, followed by induction, we get -

${\displaystyle \cos {\frac {\pi }{255\times 2^{0}}}={\frac {\sqrt {2+2\cos({\frac {\pi }{15}}-{\frac {\pi }{17}})}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{255\times 2^{0}}}={\frac {\sqrt {2-2\cos({\frac {\pi }{15}}-{\frac {\pi }{17}})}}{2}};}$

${\displaystyle \cos {\frac {\pi }{255\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{255\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{255\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{255\times 2^{n}}}}}{2}};}$

Therefore, using the radical form values from the sections above, and applying cos(A-B) = cosA cosB + sinA sinB, followed by induction, we get -

${\displaystyle \cos {\frac {\pi }{65535\times 2^{0}}}={\frac {\sqrt {2+2\cos({\frac {\pi }{255}}-{\frac {\pi }{257}})}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{65535\times 2^{0}}}={\frac {\sqrt {2-2\cos({\frac {\pi }{255}}-{\frac {\pi }{257}})}}{2}};}$

${\displaystyle \cos {\frac {\pi }{65535\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{65535\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{65535\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{65535\times 2^{n}}}}}{2}}.}$

Finally, using the radical form values from the sections above, and applying cos(A-B) = cosA cosB + sinA sinB, followed by induction, we get -

${\displaystyle \cos {\frac {\pi }{4294967295\times 2^{0}}}={\frac {\sqrt {2+2\cos({\frac {\pi }{65535}}-{\frac {\pi }{65537}})}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{4294967295\times 2^{0}}}={\frac {\sqrt {2-2\cos({\frac {\pi }{65535}}-{\frac {\pi }{65537}})}}{2}};}$

${\displaystyle \cos {\frac {\pi }{4294967295\times 2^{n+1}}}={\frac {\sqrt {2+2\cos {\frac {\pi }{4294967295\times 2^{n}}}}}{2}}}$ and ${\displaystyle \sin {\frac {\pi }{4294967295\times 2^{n+1}}}={\frac {\sqrt {2-2\cos {\frac {\pi }{4294967295\times 2^{n}}}}}{2}}.}$

The radical form expansion of the above is very large, hence expressed in the simpler form above.

n × π/(5 × 2^m)

Chord(36°) = a/b = 1/φ, i.e., the reciprocal of the golden ratio, from Ptolemy's theorem

Geometrical method

Applying Ptolemy's theorem to the cyclic quadrilateral ABCD defined by four successive vertices of the pentagon, we can find that:

${\displaystyle \operatorname {crd} 36^{\circ }=\operatorname {crd} (\angle \mathrm {ADB} )={\frac {a}{b}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}}$

which is the reciprocal 1/φ of the golden ratio. crd is the chord function,

${\displaystyle \operatorname {crd} \ {\theta }=2\sin {\frac {\theta }{2}}.\,}$

(See also Ptolemy's table of chords.)

Thus

${\displaystyle \sin 18^{\circ }={\frac {1}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{4}}.}$

(Alternatively, without using Ptolemy's theorem, label as X the intersection of AC and BD, and note by considering angles that triangle AXB is isosceles, so AX = AB = a. Triangles AXD and CXB are similar, because AD is parallel to BC. So XC = a·(a/b). But AX + XC = AC, so a + a²/b = b. Solving this gives a/b = 1/φ, as above).

Similarly

${\displaystyle \operatorname {crd} \ 108^{\circ }=\operatorname {crd} (\angle \mathrm {ABC} )={\frac {b}{a}}={\frac {1+{\sqrt {5}}}{2}},}$

so

${\displaystyle \sin 54^{\circ }=\cos 36^{\circ }={\frac {1+{\sqrt {5}}}{4}}.}$

Algebraic method

If θ is 18° or -54°, then 2θ and 3θ add up to 5θ = 90° or -270°, therefore sin 2θ is equal to cos 3θ.

${\displaystyle (2\sin \theta )\cos \theta =\sin 2\theta =\cos 3\theta =4\cos ^{3}\theta -3\cos \theta =(4\cos ^{2}\theta -3)\cos \theta =(1-4\sin ^{2}\theta )\cos \theta }$

So, ${\displaystyle 4\sin ^{2}\theta +2\sin \theta -1=0}$, which implies ${\displaystyle \sin \theta =\sin(18^{\circ },-54^{\circ })={\frac {-1\pm {\sqrt {5}}}{4}}.}$

Therefore,

${\displaystyle \sin(18^{\circ })=\cos(72^{\circ })={\frac {{\sqrt {5}}-1}{4}}}$ and ${\displaystyle \sin(54^{\circ })=\cos(36^{\circ })={\frac {{\sqrt {5}}+1}{4}}}$ and

${\displaystyle \sin(36^{\circ })=\cos(54^{\circ })={\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}$ and ${\displaystyle \sin(72^{\circ })=\cos(18^{\circ })={\frac {\sqrt {10+2{\sqrt {5}}}}{4}}.}$

Alternately, the multiple-angle formulas for functions of 5x, where x ∈ {18, 36, 54, 72, 90} and 5x ∈ {90, 180, 270, 360, 450}, can be solved for the functions of x, since we know the function values of 5x. The multiple-angle formulas are:

${\displaystyle \sin 5x=16\sin ^{5}x-20\sin ^{3}x+5\sin x,\,}$

${\displaystyle \cos 5x=16\cos ^{5}x-20\cos ^{3}x+5\cos x.\,}$

• When sin 5x = 0 or cos 5x = 0, we let y = sin x or y = cos x and solve for y:

${\displaystyle 16y^{5}-20y^{3}+5y=0.\,}$

One solution is zero, and the resulting quartic equation can be solved as a quadratic in y².

• When sin 5x = 1 or cos 5x = 1, we again let y = sin x or y = cos x and solve for y:

${\displaystyle 16y^{5}-20y^{3}+5y-1=0,\,}$

which factors into:

${\displaystyle (y-1)\left(4y^{2}+2y-1\right)^{2}=0.\,}$

n × π/20

9° is 45 − 36, and 27° is 45 − 18; so we use the subtraction formulas for sine and cosine.

n × π/30

6° is 36 − 30, 12° is 30 − 18, 24° is 54 − 30, and 42° is 60 − 18; so we use the subtraction formulas for sine and cosine.

n × π/60

3° is 18 − 15, 21° is 36 − 15, 33° is 18 + 15, and 39° is 54 − 15, so we use the subtraction (or addition) formulas for sine and cosine.

Strategies for simplifying expressions

Rationalizing the denominator

If the denominator is a square root, multiply the numerator and denominator by that radical. If the denominator is the sum or difference of two terms, multiply the numerator and denominator by the conjugate of the denominator. The conjugate is the identical, except the sign between the terms is changed. Sometimes the denominator needs to be rationalized more than once.

Splitting a fraction in two

Sometimes it helps to split the fraction into the sum of two fractions and then simplify both separately.

Squaring and taking square roots

If there is a complicated term, with only one kind of radical in a term, this plan may help. Square the term, combine like terms, and take the square root. This may leave a big radical with a smaller radical inside, but it is often better than the original.

Simplifying nested radical expressions

In general nested radicals cannot be reduced. But the radical

${\displaystyle {\sqrt {a\pm b{\sqrt {c}}}}\,}$

with a, b, and c rational, can be reduced if

${\displaystyle R={\sqrt {a^{2}-b^{2}c}}\,}$

is rational. In this case both

${\displaystyle d={\frac {a+R}{2}}{\text{ and }}e={\frac {a-R}{2}}\,}$

are rational, and we have

${\displaystyle {\sqrt {a\pm b{\sqrt {c}}}}={\sqrt {d}}\pm {\sqrt {e}}.\,}$

For example,

${\displaystyle 4\sin 18^{\circ }={\sqrt {6-2{\sqrt {5}}}}={\sqrt {5}}-1.\,}$

${\displaystyle 4\sin 15^{\circ }=2{\sqrt {2-{\sqrt {3}}}}={\sqrt {2}}\left({\sqrt {3}}-1\right).}$

See also

• Constructible polygon, one for which the cosine or sine of each angle has an exact expression in square roots
• Heptadecagonal construction, giving the exact expression for cos 2π/17
• List of trigonometric identities
• Niven's theorem on rational values of the sine of a rational multiple of π
• Ptolemy's table of chords
• Trigonometric functions
• Trigonometric number, the value of a trigonometric function of a rational multiple of π
• Units of angle measure

References

1. Bradie, Brian (Sep 2002). "Exact values for the sine and cosine of multiples of 18°: A geometric approach". The College Mathematics Journal. 33 (4): 318–319. doi:10.2307/1559057. JSTOR 1559057.

• Weisstein, Eric W. "Constructible polygon". MathWorld.

Weisstein, Eric W. "Trigonometry angles". MathWorld.

• π/3 (60°) — π/6 (30°) — π/12 (15°) — π/24 (7.5°)
• π/4 (45°) — π/8 (22.5°) — π/16 (11.25°) — π/32 (5.625°)
• π/5 (36°) — π/10 (18°) — π/20 (9°)
• π/7 — π/14
• π/9 (20°) — π/18 (10°)
• π/11
• π/13
• π/15 (12°) — π/30 (6°)
• π/17
• π/19
• π/23

• Bracken, Paul; Cizek, Jiri (2002). "Evaluation of quantum mechanical perturbation sums in terms of quadratic surds and their use in approximation of ζ(3)/π³". Int. J. Quantum Chem. 90 (1): 42–53. doi:10.1002/qua.1803.
• Conway, John H.; Radin, Charles; Sadun, Lorenzo (1999). "On angles whose squared trigonometric functions are rational". Disc. And Comp. Geom. 22 (3): 321–332. arXiv:math-ph/9812019. doi:10.1007/PL00009463. MR 1706614.
• Girstmair, Kurt (1997). "Some linear relations between values of trigonometric functions at kπ/n". Acta Arithmetica. 81 (4): 387–398. doi:10.4064/aa-81-4-387-398. MR 1472818.
• Gurak, S. (2006). "On the minimal polynomial of gauss periods for prime powers". Mathematics of Computation. 75 (256): 2021–2035. Bibcode:2006MaCom..75.2021G. doi:10.1090/S0025-5718-06-01885-0. MR 2240647.
• Servi, L. D. (2003). "Nested square roots of 2". Amer. Math. Monthly. 110 (4): 326–330. doi:10.2307/3647881. JSTOR 3647881. MR 1984573.

External links

• Constructible Regular Polygons
• Naming polygons
• Sine and cosine in surds includes alternative expressions in some cases as well as expressions for some other angles