List of metaphor-based metaheuristics

This is a chronologically ordered list of metaphor-based metaheuristics and swarm intelligence algorithms.

Algorithms

Simulated annealing (Kirkpatrick et al., 1983)

Simulated annealing (SA) is a probabilistic technique inspired by a heat treatment method in metallurgy. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For problems where finding the precise global optimum is less important than finding an acceptable local optimum in a fixed amount of time, simulated annealing may be preferable to alternatives such as gradient descent.

Simulated annealing interprets slow cooling as a slow decrease in the probability of accepting worse solutions as it explores the solution space. Accepting worse solutions is a fundamental property of metaheuristics because it allows for a more extensive search for the optimal solution.

Ant colony optimization (Dorigo, 1992)

The ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Initially proposed by Marco Dorigo in 1992 in his PhD thesis,[1][2] the first algorithm was aiming to search for an optimal path in a graph, based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants. From a broader perspective, ACO performs a model-based search[3] and shares some similarities with Estimation of Distribution Algorithms.

Particle swarm optimization (Kennedy & Eberhart, 1995)

Particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formulae over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.

PSO is originally attributed to Kennedy, Eberhart and Shi[4][5] and was first intended for simulating social behaviour,[6] as a stylized representation of the movement of organisms in a bird flock or fish school. The algorithm was simplified and it was observed to be performing optimization. The book by Kennedy and Eberhart[7] describes many philosophical aspects of PSO and swarm intelligence. An extensive survey of PSO applications is made by Poli.[8][9] Recently, a comprehensive review on theoretical and experimental works on PSO has been published by Bonyadi and Michalewicz.[10]

Harmony search (Geem, Kim & Loganathan, 2001)

Harmony search is a phenomenon-mimicking metaheuristic introduced in 2001 by Zong Woo Geem, Joong Hoon Kim, and G. V. Loganathan.[11] Harmony search is inspired by the improvisation process of jazz musicians. A paper claimed that harmony search is proven to be a special case of the Evolution Strategies algorithm. [12] However, a recent paper argues that the structure of Evolution Strategies is different from that of harmony search. [13] Also, a programming code was provided for showing how HS to solve Sudoku.[14]

The Harmony search (HS) is a relatively simple yet very efficient evolutionary algorithm. In HS algorithm a set of possible solutions is randomly generated (called Harmony memory). A new solution is generated by using all the solutions in the Harmony memory (rather than just two as used in GA) and if this new solution is better than the Worst solution in Harmony memory, the Worst solution gets replaced by this new solution. Although HS is a relatively new meta heuristic algorithm, its effectiveness and advantages have been demonstrated in various applications like design of municipal water distribution networks,[15] structural design,[16] traffic routing,[17] load dispatch problem in electrical engineering,[18] multi objective optimization,[19] rostering problems,[20] clustering,[21] classification and feature selection[22][23] to name a few. A detailed survey on applications of HS can be found in [24][25] and applications of HS in data mining can be found in.[26]

Artificial bee colony algorithm (Karaboga, 2005)

Artificial bee colony algorithm is a meta-heuristic algorithm introduced by Karaboga in 2005,[27] and simulates the foraging behaviour of honey bees. The ABC algorithm has three phases: employed bee, onlooker bee and scout bee. In the employed bee and the onlooker bee phases, bees exploit the sources by local searches in the neighbourhood of the solutions selected based on deterministic selection in the employed bee phase and the probabilistic selection in the onlooker bee phase. In the scout bee phase which is an analogy of abandoning exhausted food sources in the foraging process, solutions that are not beneficial anymore for search progress are abandoned, and new solutions are inserted instead of them to explore new regions in the search space. The algorithm has a well-balanced exploration and exploitation ability.

Bees algorithm (Pham, 2005)

The bees algorithm in its basic formulation was created by Pham and his co-workers in 2005,[28] and further refined in the following years.[29] Modelled on the foraging behaviour of honey bees, the algorithm combines global explorative search with local exploitative search. A small number of artificial bees (scouts) explores randomly the solution space (environment) for solutions of high fitness (highly profitable food sources), whilst the bulk of the population search (harvest) the neighbourhood of the fittest solutions looking for the fitness optimum. A deterministics recruitment procedure which simulates the waggle dance of biological bees is used to communicate the scouts' findings to the foragers, and distribute the foragers depending on the fitness of the neighbourhoods selected for local search. Once the search in the neighbourhood of a solution stagnates, the local fitness optimum is considered to be found, and the site is abandoned. In summary, the Bees Algorithm searches concurrently the most promising regions of the solution space, whilst continuously sampling it in search of new favourable regions.

Glowworm swarm optimization (Krishnanand & Ghose, 2005)

The glowworm swarm optimization is a swarm intelligence optimization algorithm developed based on the behaviour of glowworms (also known as fireflies or lightning bugs). The GSO algorithm was developed and introduced by K.N. Krishnanand and Debasish Ghose in 2005 at the Guidance, Control, and Decision Systems Laboratory in the Department of Aerospace Engineering at the Indian Institute of Science, Bangalore, India.[30]

The behaviour pattern of glowworms which is used for this algorithm is the apparent capability of the glowworms to change the intensity of the luciferin emission and thus appear to glow at different intensities.

1. The GSO algorithm makes the agents glow at intensities approximately proportional to the function value being optimized. It is assumed that glowworms of brighter intensities attract glowworms that have lower intensity.
2. The second significant part of the algorithm incorporates a dynamic decision range by which the effect of distant glowworms are discounted when a glowworm has sufficient number of neighbours or the range goes beyond the range of perception of the glowworms.

The part 2 of the algorithm makes it different from other evolutionary multimodal optimization algorithms. It is this step that allows glowworm swarms to automatically subdivide into subgroups which can then converge to multiple local optima simultaneously, This property of the algorithm allows it to be used to identify multiple peaks of a multi-modal function and makes it a part of the evolutionary multimodal optimization algorithms family.

Shuffled frog leaping algorithm (Eusuff, Lansey & Pasha, 2006)

The shuffled frog leaping algorithm is an optimization algorithm used in artificial intelligence.[31] It is comparable to a genetic algorithm.

Cat Swarm Optimization (Chu, Tsai, and Pan, 2006)

The cat swarm optimization algorithm which solves optimization problems and is inspired by the behavior of cats.[32] It is similar to other swarm optimization algorithms such as the Ant Colony Optimization or Particle Swarm Optimization algorithms. Seeking and Tracing, two common behavior of cats, make up the two sub-models of the algorithm. Seeking Mode is inspired by the behavior of a cat at rest, seeking where to move next. In Seeking Mode, it selects several candidate points and then selects one to move to randomly, increasing the probability of choosing points that have a higher fitness value. Tracing Mode is inspired by a cat tracing some target. In this mode, the cat will try to move towards the position with the best fitness value. Cats will continue moving in Seeking and Tracing mode until a terminating condition is met.

Imperialist competitive algorithm (Atashpaz-Gargari & Lucas, 2007)

The imperialist competitive algorithm is a computational method that is used to solve optimization problems of different types.[33][34] Like most of the methods in the area of evolutionary computation, ICA does not need the gradient of the function in its optimization process. From a specific point of view, ICA can be thought of as the social counterpart of genetic algorithms (GAs). ICA is the mathematical model and the computer simulation of human social evolution, while GAs are based on the biological evolution of species.

This algorithm starts by generating a set of random candidate solutions in the search space of the optimization problem. The generated random points are called the initial Countries. Countries in this algorithm are the counterpart of Chromosomes in GAs and Particles in Particle Swarm Optimization (PSO) and it is an array of values of a candidate solution of optimization problem. The cost function of the optimization problem determines the power of each country. Based on their power, some of the best initial countries (the countries with the least cost function value), become Imperialists and start taking control of other countries (called colonies) and form the initial Empires.[33]

Two main operators of this algorithm are Assimilation and Revolution. Assimilation makes the colonies of each empire get closer to the imperialist state in the space of socio-political characteristics (optimization search space). Revolution brings about sudden random changes in the position of some of the countries in the search space. During assimilation and revolution a colony might reach a better position and has the chance to take the control of the entire empire and replace the current imperialist state of the empire.[35]

Imperialistic Competition is another part of this algorithm. All the empires try to win this game and take possession of colonies of other empires. In each step of the algorithm, based on their power, all the empires have a chance to take control of one or more of the colonies of the weakest empire.[33]

Algorithm continues with the mentioned steps (Assimilation, Revolution, Competition) until a stop condition is satisfied.

The above steps can be summarized as the below pseudocode.[34][35]

0) Define objective function: ${\displaystyle f(\mathbf {x} ),\quad \mathbf {x} =(x_{1},x_{2},\dots ,x_{d});\,}$
1) Initialization of the algorithm. Generate some random solution in the search space and create initial empires.
    2) Assimilation: Colonies move towards imperialist states in different in directions.
    3) Revolution: Random changes occur in the characteristics of some countries.
    4) Position exchange between a colony and Imperialist. A colony with a better position than the imperialist,
       has the chance to take the control of empire by replacing the existing imperialist.
    5) Imperialistic competition: All imperialists compete to take possession of colonies of each other.
    6) Eliminate the powerless empires. Weak empires lose their power gradually and they will finally be eliminated.
    7) If the stop condition is satisfied, stop, if not go to 2.
8) End

River formation dynamics (Rabanal, Rodríguez & Rubio, 2007)

River formation dynamics is based on imitating how water forms rivers by eroding the ground and depositing sediments (the drops act as the swarm). After drops transform the landscape by increasing/decreasing the altitude of places, solutions are given in the form of paths of decreasing altitudes. Decreasing gradients are constructed, and these gradients are followed by subsequent drops to compose new gradients and reinforce the best ones. This heuristic optimization method was first presented in 2007 by Rabanal et al.[36] The applicability of RFD to other NP-complete problems has been studied,[37] and the algorithm has been applied to fields such as routing[38] and robot navigation.[39] The main applications of RFD can be found at a detailed survey.[40]

Intelligent water drops algorithm (Shah-Hosseini, 2007)

Intelligent water drops algorithm contains a few essential elements of natural water drops and actions and reactions that occur between river's bed and the water drops that flow within. The IWD was first introduced for the traveling salesman problem in 2007.[41]

Almost every IWD algorithm is composed of two parts: a graph that plays the role of distributed memory on which soils of different edges are preserved, and the moving part of the IWD algorithm, which is a few number of Intelligent water drops. These intelligent water drops (IWDs) both compete and cooperate to find better solutions and by changing soils of the graph, the paths to better solutions become more reachable. It is mentioned that the IWD-based algorithms need at least two IWDs to work.

The IWD algorithm has two types of parameters: static and dynamic parameters. Static parameters are constant during the process of the IWD algorithm. Dynamic parameters are reinitialized after each iteration of the IWD algorithm. The pseudo-code of an IWD-based algorithm may be specified in eight steps:

1) Static parameter initialization

a) Problem representation in the form of a graph

b) Setting values for static parameters

2) Dynamic parameter initialization: soil and velocity of IWDs

3) Distribution of IWDs on the problem's graph

4) Solution construction by IWDs along with soil and velocity updating

a) Local soil updating on the graph

b) Soil and velocity updating on the IWDs

5) Local search over each IWD's solution (optional)

6) Global soil updating

7) Total-best solution updating

8) Go to step 2 unless termination condition is satisfied

Gravitational search algorithm (Rashedi, Nezamabadi-pour & Saryazdi, 2009)

A gravitational search algorithm is based on the law of gravity and the notion of mass interactions. The GSA algorithm uses the theory of Newtonian physics and its searcher agents are the collection of masses. In GSA, there is an isolated system of masses. Using the gravitational force, every mass in the system can see the situation of other masses. The gravitational force is therefore a way of transferring information between different masses (Rashedi, Nezamabadi-pour and Saryazdi 2009).[42] In GSA, agents are considered as objects and their performance is measured by their masses. All these objects attract each other by a gravity force, and this force causes movement of all objects towards the objects with heavier masses. Heavier masses correspond to better solutions of the problem. The position of the agent corresponds to a solution of the problem, and its mass is determined using a fitness function. By lapse of time, masses are attracted by the heaviest mass, which would ideally present an optimum solution in the search space. The GSA could be considered as an isolated system of masses. It is like a small artificial world of masses obeying the Newtonian laws of gravitation and motion.[43] A multi-objective variant of GSA, called MOGSA, was first proposed by Hassanzadeh et al. in 2010.[44]

Cuckoo search (Yang & Deb, 2009)

In operations research, cuckoo search is an optimization algorithm developed by Xin-she Yang and Suash Deb in 2009.[45][46] It was inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of other host birds (of other species). If a host bird discovers that the eggs are not their own, it will throw them out of the nest, or abandon the nest and build a new one. The principle of cuckoo search is placing "eggs" (newly found solutions) into "nests", and keeping the best ones as candidates for the next generation. The new solutions may be randomly discarded ("eggs" are being thrown out of the "nest").

Bat algorithm (Yang, 2010)

Bat algorithm is a swarm-intelligence-based algorithm, inspired by the echolocation behavior of microbats. BA automatically balances exploration (long-range jumps around the global search space to avoid getting stuck around one local maximum) with exploitation (searching in more detail around known good solutions to find local maxima) by controlling loudness and pulse emission rates of simulated bats in the multi-dimensional search space.[47]

Spiral optimization (SPO) algorithm (Tamura & Yasuda 2011, 2016-2017)

Spiral optimization (SPO) algorithm

The spiral optimization (SPO) algorithm is an uncomplicated search concept inspired by spiral phenomena in nature. The motivation for focusing on spiral phenomena was due to the insight that the dynamics that generate logarithmic spirals share the diversification and intensification behavior. The diversification behavior can work for a global search (exploration) and the intensification behavior enables an intensive search around a current found good solution (exploitation). The SPO algorithm is a multipoint search algorithm that has no objective function gradient, which uses multiple spiral models that can be described as deterministic dynamical systems. As search points follow logarithmic spiral trajectories towards the common center, defined as the current best point, better solutions can be found and the common center can be updated.[48]

Flower pollination algorithm (Yang, 2012)

Flower pollination algorithm is a metaheuristic algorithm that was developed by Xin-She Yang,[49] based on the pollination process of flowering plants.

This algorithm has 4 rules or assumptions:

1. Biotic and cross-pollination is considered as a global pollination process with pollen carrying pollinators performing Levy flights.
2. Abiotic and self-pollination are considered as local pollination.
3. Flower constancy can be considered as the reproduction probability is proportional to the similarity of two flowers involved.
4. Local and global pollination are controlled by a switch probability ${\displaystyle p\in [0,1]}$. Due to the physical proximity and other factors such as wind, local pollination can have a significant fraction q in the overall pollination activities.

These rules can be translated into the following updating equations:

${\displaystyle x_{i}^{t+1}=x_{i}^{t}+L(x_{i}^{t}-g_{*})}$

${\displaystyle x_{i}^{t+1}=x_{i}^{t}+\epsilon (x_{i}^{t}-x_{k}^{t})}$

where ${\displaystyle x_{i}^{t}}$ is the solution vector and ${\displaystyle g_{*}}$ is the current best found so far during iteration. The switch probability between two equations during iterations is ${\displaystyle p}$. In addition, ${\displaystyle \epsilon }$ is a random number drawn from a uniform distribution. ${\displaystyle L}$ is a step size drawn from a Lévy distribution.

Lévy flights using Lévy steps is a powerful random walk because both global and local search capabilities can be carried out at the same time. In contrast with standard Random walks, Lévy flights have occasional long jumps, which enable the algorithm to jump out any local valleys. Lévy steps obey the following approximation:

${\displaystyle L\sim {\frac {1}{s^{1+\beta }}},}$

where ${\displaystyle \beta }$ is the Lévy exponent.[50] It may be challenging to draw Lévy steps properly, and a simple way of generating Lévy flights ${\displaystyle s}$ is to use two normal distributions ${\displaystyle u}$ and ${\displaystyle v}$ by a transform[51]

${\displaystyle s={\frac {u}{|v|^{1+\beta }}},}$

with

${\displaystyle u\sim N(0,\sigma ^{2}),\quad v\sim N(0,1),}$

where ${\displaystyle \sigma }$ is a function of ${\displaystyle \beta }$.

Cuttlefish optimization algorithm (Eesa, Mohsin, Brifcani & Orman, 2013)

The six cases of reflection used by the Cuttlefish

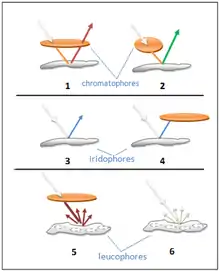
The cuttlefish optimization algorithm is a population-based search algorithm inspired by skin color changing behaviour of Cuttlefish which was developed in 2013[52][53] It has two global search and two local search.

The algorithm considers two main processes: Reflection and Visibility. Reflection process simulates the light reflection mechanism, while visibility simulates the visibility of matching patterns. These two processes are used as a search strategy to find the global optimal solution. The formulation of finding the new solution (newP) by using reflection and visibility is as follows: ${\displaystyle newP=Reflection+Visibility}$

CFA divide the population into 4 Groups (G1, G2, G3 and G4). For G1 the algorithm applying case 1 and 2 (the interaction between chromatophores and iridophores) to produce a new solutions. These two cases are used as a global search. For G2, the algorithm uses case 3 (Iridophores reflection opaerator) and case 4 (the interaction between Iridophores and chromatophores) to produces a new solutions) as a local search. While for G3 the interaction between the leucophores and chromatophores (case 5) is used to produce solutions around the best solution (local search). Finally for G4, case 6 (reflection operator of leucophores) is used as a global search by reflecting any incoming light as it with out any modification. The main step of CFA is described as follows:

algorithm cuttlefish_optimization is
    Initialize population (P[N]) with random solutions, Assign the values of r1, r2, v1, v2.
    Evaluate the population and keep the best solution.
    Divide population into four groups (G1, G2, G3 and G4).

    repeat
        Calculate the average value of the best solution.
        for each element in G1 do
            generate new solution using Case(1 and 2)
        for each element in G2 do
            generate new solution using Case(3 and 4)
        for each element in G3 do
            generate new solution using Case(5)
        for each element in G4 do
            generate new solution using Case(6)
        Evaluate the new solutions 
    until (stopping criterion is met)

    return the best solution

Equations that are used to calculate reflection and visibility for the four Groups are described below:

Case 1 and 2 for G1:

${\displaystyle Reflection[j]=R*G_{1}[j].Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-G_{1}[i].Points[j])}$

Case 3 and 4 for G2:

${\displaystyle Reflection[j]=R*Best.Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-G_{2}[i].Points[j])}$

Case 5 for G3:

${\displaystyle Reflection[j]=R*Best.Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-AV_{Best}}$

Case 6 for G4:

${\displaystyle P[i].Points[j]=random*(upperLimit-lowerLinit)+LowerLimit,i=1,2,...,N;j=1,2,...,d}$

Where ${\displaystyle G_{1}}$, ${\displaystyle G_{2}}$ are Group1 and Group2, i presents the ${\displaystyle i^{th}}$ element in G, j is the ${\displaystyle j^{th}}$ point of ${\displaystyle i^{th}}$ element in group G, Best is the best solution and ${\displaystyle AV_{Best}}$ presents the average value of the Best points. While R and V are two random numbers produced around zero such as between (-1, 1), R represents the degree of reflection, V represents the visibility degree of the final view of the pattern, upperLimit and lowerLimit are the upper limit and the lower limit of the problem domain.

Heterogeneous Distributed Bees Algorithm (Tkach et al., 2013)

The Heterogeneous Distributed Bees Algorithm (HDBA) also known as the Modified Distributed Bees Algorithm (MDBA) is a multi-agent metaheuristic algorithm initially introduced by Tkach and his co-workers in 2013,[54][55] developed as part of his PhD dissertation. HDBA uses probabilistic technique taking inspiration from the foraging behaviour of bees. It enables to solve combinatorial optimization problems with multiple heterogeneous agents that possess different capabilities and performances. The final decision-making mechanism uses a wheel-selection rule, where each agent has a probability with which it selects a solution. It was first applied for the case of heterogeneous sensors in target recognition problem to improve system performance by correlating sensors’ utility function with the value of their performances. Afterwards, it was successfully applied to other problems, including the problem of allocating police agents to crime incidents and producing near-optimal solutions to the travelling salesman problem.

Artificial ecosystem algorithm (Baczyński, 2013)

Artificial ecosystem algorithm (AEA) is a probabilistic optimisation method inspired by some phenomena taking place in natural ecosystems. Relationships between individuals is modelled both by their mutual relationships within a single group and the relationships between individuals belonging to different groups, co-existing as a part of the ecological system. There are three principal types of organisms: plants, herbivores and predators. All types of organisms reproduce (cross over and mutate) within their own species. As a method, it includes some of Evolutionary Algorithms and PSO elements with additional extensions. It is quite complicated method, but it has proved itself to be capable to solve both continuous and combinatorial optimization problems.[56]

Cooperative Group Optimization (2014)

Cooperative group optimization (CGO) system[57][58] is a metaheuristic framework for implementing algorithm instances by integrating the advantages of the cooperative group and low-level algorithm portfolio design. Following the nature-inspired paradigm of a cooperative group, the agents not only explore in a parallel way with their individual memory, but also cooperate with their peers through the group memory. Each agent holds a portfolio of (heterogeneous) embedded search heuristics (ESHs), in which each ESH can drive the group into a stand-alone CGO case, and hybrid CGO cases in an algorithmic space can be defined by low-level cooperative search among an algorithm portfolio (of ESHs) through customized memory sharing. The optimization process might also be facilitated by a passive group leader through encoding knowledge in the search landscape. It has been applied on both numerical and combinatorial optimization problems.

Artificial swarm intelligence (Rosenberg, 2014)

Artificial swarm intelligence refers to a real-time closed-loop system of human users connected over the internet and structured in a framework modeled after natural swarms such that it evokes the group's collective wisdom as a unified emergent intelligence.[59][60] In this way, human swarms can answer questions, make predictions, reach decisions, and solve problems by collectively exploring a diverse set of options and converging on preferred solutions in synchrony. Invented by Dr. Louis Rosenberg in 2014, the ASI methodology has become notable for its ability to make accurate collective predictions that outperform the individual members of the swarm.[61] In 2016 an Artificial Swarm Intelligence from Unanimous A.I. was challenged by a reporter to predict the winners of the Kentucky Derby, and successfully picked the first four horses, in order, beating 540 to 1 odds.[62][63]

Colliding bodies optimization (Kaveh and Mahdavi, 2014)

The Colliding bodies optimization (CBO)[64] algorithm was created by Kaveh and Mahdavi in 2014 based on laws of momentum and energy. This algorithm does not depend on any internal parameter and also it is extremely simple to implement and to use and used in different types of problems in engineering.[65]

Duelist Algorithm (Biyanto, 2016)

Duelist algorithm refers to a gene-based optimization algorithm similar to Genetic Algorithms. Duelist Algorithm starts with an initial set of duelists. The duel is to determine the winner and loser. The loser learns from the winner, while the winner try their new skill or technique that may improve their fighting capabilities. A few duelists with highest fighting capabilities are called as champion. The champion train a new duelist such as their capabilities. The new duelist will join the tournament as a representative of each champion. All duelist are re-evaluated, and the duelists with worst fighting capabilities is eliminated to maintain the amount of duelists.[66]

Harris hawks optimization (Heidari et al., 2019)

Harris hawks optimizer (HHO) inspires the hunting strategies of Harris's hawk and escaping patterns of rabbits in nature.[67]

Killer Whale Algorithm (Biyanto, 2016)

Killer Whale Algorithm is an algorithm Inspired by the Killer Whale Life. The philosophy of algorithm is the patterns of movement Killer Whale in prey hunting and Killer whale social structure. The novelty of this algorithm is incorporating "memorize capability" of Killer Whale in the algorithm.[68]

Rain Water Algorithm (Biyanto, 2017)

"Physical movements of rain drops by utilizing Newton's Law motion" was inspired the authors to create this algorithm. Each rain drop represent as random values of optimized variables that it have vary in mass and elevation. It will fall on the ground by following "the free fall movement" with velocity is square root of gravity acceleration time elevation. The next movement is "uniformly accelerated motion" along the rain drop travel to reach the lowest place on the ground. The lowest place in the ground is an objective function of this algorithm.[69]

Mass and Energy Balances Algorithm (Biyanto, 2018)

Mass and Energy Balances is a fundamental "laws of physics" states that mass can neither be produced nor destroyed. It is only conserved. Equally fundamental is the law of conservation of energy. Although energy can change in form, it can not be created or destroyed also. The beauty of this algorithm is the capability to reach the global optimum solution by simultaneously work either "minimize and maximize searching method".

Hydrological Cycle Algorithm (Wedyan et al., 2017)

A new nature-inspired optimization algorithm called the Hydrological Cycle Algorithm (HCA) is proposed based on the continuous movement of water in nature. In the HCA, a collection of water drops passes through various hydrological water cycle stages, such as flow, evaporation, condensation, and precipitation. Each stage plays an important role in generating solutions and avoiding premature convergence. The HCA shares information by direct and indirect communication among the water drops, which improves solution quality. HCA provides an alternative approach to tackling various types of optimization problems as well as an overall framework for water-based particle algorithms in general.[70]

Emperor Penguins Colony (Harifi et al., 2019)

This algorithm is a new metaheuristic algorithm that inspired by the behavior of emperor penguins that live in Antarctica. EPC is controlled by the body heat radiation of the penguins and their spiral-like movement in their colony. The emperor penguins in the colony seek to create the appropriate heat and regulate their body temperature, and this heat is completely coordinated and controlled by the movement of the penguins.[71]

Momentum Balance Algorithm (MBA) (Biyanto et al., 2019)

Momentum balance is one of three fundamental "laws of physics" that states mass, energy and momentum is only conserved. The utilizations of momentum balance have been proposed in many applications.[72][73][74]

In this research, momentum balance was adopted to obtain the perfectly elastic collision. In an ideal, perfectly elastic collision, there is no kinetic energy losses into other forms such as potential energy, heat and noise. The beauty of this algorithm is easy as simple as deterministic optimization algorithms, however the momentum balance algorithm has capability to reach the global optimum solution.

Shuffled Shepherd Optimization Algorithm (SSOA) (Kaveh and Zaerreza, 2020)

This method is a new multi-community meta-heuristic optimization algorithm. In this algorithm,The agents are first separated into multi-communities and the optimization process is then performed mimicking the behavior of a shepherd in nature operating on each community.[75]

A mayfly optimization algorithm (MA) (Zervoudakis & Tsafarakis, 2020)

The mayfly optimization algorithm was developed to address both continuous and discrete optimization problems and is inspired from the flight behavior and the mating process of mayflies. The processes of nuptial dance and random flight enhance the balance between the algorithm's exploration and exploitation properties and assist its escape from local optima. The performance of the mayfly algorithm is superior to that of other popular metaheuristics like PSO, DE, GA and FA, in terms of convergence rate and convergence speed. [76]

Political Optimizer (PO) (Qamar Askari, Irfan Younas & Mehreen Saeed, 2020)

Political Optimizer (PO) is a human social behavior-based algorithm inspired by a multi-party political system. The source of inspiration is formulated as a set of 5 phases: party formation and constituency allocation, party switching, election campaign, inter-party election, and parliamentary affairs. PO has two unique features: logical division of the population to assign a dual role to each candidate solution and recent-past based position updating strategy (RPPUS). PO demonstrates excellent performance against 15 well-known meta-heuristics for 50 unimodal and multimodal benchmark functions and 4 engineering problems. [77]

Heap-Based Optimizer (HBO) (Qamar Askari, Mehreen Saeed, Irfan Younas, 2020)

HBO is a human social-behavior-based meta-heuristic inspired by the corporate rank hierarchy and interaction among the employees arranged in the hierarchy. The uniqueness of HBO is the utilization of the heap data structure to model the hierarchical arrangement of the employees and the introduction of a parameter (γ) to alternatively incorporate exploration and exploitation. Moreover, three equations derived for three phases of HBO are probabilistically merged to balance exploration and exploitation. HBO demonstrates tremendous performance for 97 benchmarks and 3 mechanical engineering problems. [78]

Forensic-based investigation algorithm (FBI) (JS Chou and NM Nguyen, 2020)

The main motivation for developing a new algorithm is its capacity to effectively and efficiently solve various optimization problems. A novel optimization method, the forensic-based investigation algorithm (FBI), is developed to determine global solutions for continuous nonlinear functions with low computational effort and high accuracy. FBI is inspired by the suspect investigation–location–pursuit process of police officers. Main features of FBI: (1) FBI is a parameter-free optimization algorithm; (2) FBI remarkably outperformed the well-known and newly developed algorithms; (3) FBI has short computational time and rapidly reaches the optimal solutions in solving problems; (4) FBI is effective in solving high-dimensional problems (D=1000); and (5) FBI structure has two teams that well balance exploration and exploitation.

Details can be found at: Chou J-S, Nguyen N-M, FBI inspired meta-optimization, Applied Soft Computing, 2020:106339, ISSN 1568-4946, https://doi.org/10.1016/j.asoc.2020.106339 [79]

Jellyfish Search (JS) (JS Chou and DN Truong, 2021)

Visualization of JS for searching the global minimum of a mathematical function.

Jellyfish Search (JS) Optimizer is inspired by the behavior of jellyfish in the ocean. The simulation of the search behavior of jellyfish involves their following the ocean current, their motions inside a jellyfish swarm (active motions and passive motions), a time control mechanism for switching among these movements, and their convergences into jellyfish bloom. The new algorithm is successfully tested on benchmark functions and optimization problems. Notably, JS has only two control parameters, which are population size and number of iterations. Therefore, JS is very simple to use, and potentially an excellent metaheuristic algorithm for solving optimization problems. [80]

Golden Eagle Optimizer (GEO) (Mohammadi-Balani et al., 2020)

Golden Eagle Optimizer (GEO) is a population-based swarm-intelligence nature-inspired metaheuristic algorithm, which is by the hunting behavior of golden eagles. The algorithm models this behavior by dividing the velocity vector of golden eagles into to components: a) attack vector, and b) cruise vector. The attack vector for each golden eagle (search agent) starts at the current position the golden eagle and ends at the location of prey in the memory of each golden eagle. The prey for each golden eagle is the best location that it has visited so far. Golden eagles circle around the prey in hypothetical hyperspheres. The cruise vector is a vector tangent to the hypothetical hypersphere for each golden eagle. The original paper contains both single- and multi-objective versions of the algorithm.[81] Source code, toolbox, and graphical user interface for Golden Eagle Optimizer (GEO) and Multi-Objective Golden Eagle Optimizer (MOGEO) are also developed for MATLAB.[82]

Criticism of the metaphor methodology

While individual metaphor-inspired metaheuristics have produced remarkably effective solutions to specific problems,[83] metaphor-inspired metaheuristics in general have attracted criticism in the research community for hiding their lack of effectiveness or novelty behind an elaborate metaphor.[83][84] Kenneth Sörensen noted that:[85]

In recent years, the field of combinatorial optimization has witnessed a true tsunami of "novel" metaheuristic methods, most of them based on a metaphor of some natural or man-made process. The behavior of virtually any species of insects, the flow of water, musicians playing together – it seems that no idea is too far-fetched to serve as inspiration to launch yet another metaheuristic. [I] will argue that this line of research is threatening to lead the area of metaheuristics away from scientific rigor.

Sörensen and Glover stated that:[86]

A large (and increasing) number of publications focuses on the development of (supposedly) new metaheuristic frameworks based on metaphors. The list of natural or man-made processes that has been used as the basis for a metaheuristic framework now includes such diverse processes as bacterial foraging, river formation, biogeography, musicians playing together, electromagnetism, gravity, colonization by an empire, mine blasts, league championships, clouds, and so forth. An important subcategory is found in metaheuristics based on animal behavior. Ants, bees, bats, wolves, cats, fireflies, eagles, dolphins, frogs, salmon, vultures, termites, flies, and many others, have all been used to inspire a "novel" metaheuristic. [...] As a general rule, publication of papers on metaphor-based metaheuristics has been limited to second-tier journals and conferences, but some recent exceptions to this rule can be found. Sörensen (2013) states that research in this direction is fundamentally flawed. Most importantly, the author contends that the novelty of the underlying metaphor does not automatically render the resulting framework "novel". On the contrary, there is increasing evidence that very few of the metaphor-based methods are new in any interesting sense.

In response, Springer's Journal of Heuristics has updated their editorial policy to state that:[87]

Proposing new paradigms is only acceptable if they contain innovative basic ideas, such as those that are embedded in classical frameworks like genetic algorithms, tabu search, and simulated annealing. The Journal of Heuristics avoids the publication of articles that repackage and embed old ideas in methods that are claimed to be based on metaphors of natural or manmade systems and processes. These so-called "novel" methods employ analogies that range from intelligent water drops, musicians playing jazz, imperialist societies, leapfrogs, kangaroos, all types of swarms and insects and even mine blast processes (Sörensen, 2013). If a researcher uses a metaphor to stimulate his or her own ideas about a new method, the method must nevertheless be translated into metaphor-free language, so that the strategies employed can be clearly understood, and their novelty is made clearly visible. (See items 2 and 3 below.) Metaphors are cheap and easy to come by. Their use to "window dress" a method is not acceptable."

[...] Implementations should be explained by employing standard optimization terminology, where a solution is called a "solution" and not something else related to some obscure metaphor (e.g., harmony, flies, bats, countries, etc.).

[...] The Journal of Heuristics fully endorses Sörensen's view that metaphor-based “novel” methods should not be published if they cannot demonstrate a contribution to their field. Renaming existing concepts does not count as a contribution. Even though these methods are often called “novel”, many present no new ideas, except for the occasional marginal variant of an already existing methodology. These methods should not take the journal space of truly innovative ideas and research. Since they do not use the standard optimization vocabulary, they are unnecessarily difficult to understand.

The policy of Springer's journal 4OR - A Quarterly Journal of Operations Research states that:[88]

The emphasis on scientific rigor and on innovation implies, in particular, that the journal does not publish articles that simply propose disguised variants of known methods without adequate validation (e.g., metaheuristics that are claimed to be "effective" on the sole basis of metaphorical comparisons with natural or artificial systems and processes). New methods must be presented in metaphor-free language by establishing their relationship with classical paradigms. Their properties must be established on the basis of scientifically compelling arguments: mathematical proofs, controlled experiments, objective comparisons, etc.

See also

• Swarm intelligence#Algorithms

Notes

1. Colorni, Alberto; Dorigo, Marco; Maniezzo, Vittorio (1992). "Distributed Optimization by Ant Colonies". In Varela, Francisco J.; Bourgine, Paul (eds.). Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life. pp. 134–42. ISBN 978-0-262-72019-9.
2. M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy, 1992.
3. Zlochin, Mark; Birattari, Mauro; Meuleau, Nicolas; Dorigo, Marco (2004). "Model-Based Search for Combinatorial Optimization: A Critical Survey". Annals of Operations Research. 131 (1–4): 373–95. CiteSeerX 10.1.1.3.427. doi:10.1023/B:ANOR.0000039526.52305.af. S2CID 63137.
4. Kennedy, J.; Eberhart, R. (1995). "Particle swarm optimization". Proceedings of ICNN'95 - International Conference on Neural Networks. 4. pp. 1942–8. CiteSeerX 10.1.1.709.6654. doi:10.1109/ICNN.1995.488968. ISBN 978-0-7803-2768-9. S2CID 7367791.
5. Shi, Y.; Eberhart, R. (1998). "A modified particle swarm optimizer". 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360). pp. 69–73. doi:10.1109/ICEC.1998.699146. ISBN 978-0-7803-4869-1. S2CID 16708577.
6. Kennedy, J. (1997). "The particle swarm: Social adaptation of knowledge". Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC '97). pp. 303–8. doi:10.1109/ICEC.1997.592326. ISBN 978-0-7803-3949-1. S2CID 61487376.
7. Kennedy, J.; Eberhart, R.C. (2001). Swarm Intelligence. Morgan Kaufmann. ISBN 978-1-55860-595-4.
8. Poli, R. (2007). "An analysis of publications on particle swarm optimisation applications" (PDF). Technical Report CSM-469. Department of Computer Science, University of Essex, UK. Archived from the original (PDF) on 2011-07-16. Retrieved 2016-08-31.
9. Poli, Riccardo (2008). "Analysis of the Publications on the Applications of Particle Swarm Optimisation". Journal of Artificial Evolution and Applications. 2008: 1–10. doi:10.1155/2008/685175.
10. Bonyadi, Mohammad Reza; Michalewicz, Zbigniew (2017). "Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review". Evolutionary Computation. 25 (1): 1–54. doi:10.1162/EVCO_r_00180. PMID 26953883. S2CID 8783143.
11. Zong Woo Geem; Joong Hoon Kim; Loganathan, G.V. (2016). "A New Heuristic Optimization Algorithm: Harmony Search". Simulation. 76 (2): 60–8. doi:10.1177/003754970107600201. S2CID 20076748.
12. Weyland, Dennis (2015). "A critical analysis of the harmony search algorithm—How not to solve sudoku". Operations Research Perspectives. 2: 97–105. doi:10.1016/j.orp.2015.04.001.
13. Saka, M. (2016). "Metaheuristics in structural optimization and discussions on harmony search algorithm". Swarm and Evolutionary Computation. 28: 88–97. doi:10.1016/j.swevo.2016.01.005.
14. "HS Code for Sudoku".
15. Geem, Zong Woo (2006). "Optimal cost design of water distribution networks using harmony search". Engineering Optimization. 38 (3): 259–277. doi:10.1080/03052150500467430. S2CID 18614329.
16. Gholizadeh, S.; Barzegar, A. (2013). "Shape optimization of structures for frequency constraints by sequential harmony search algorithm". Engineering Optimization. 45 (6): 627. Bibcode:2013EnOp...45..627G. doi:10.1080/0305215X.2012.704028. S2CID 123589002.
17. Geem, Zong Woo; Lee, Kang Seok; Park, Yongjin (2005). "Application of Harmony Search to Vehicle Routing". American Journal of Applied Sciences. 2 (12): 1552. doi:10.3844/ajassp.2005.1552.1557.
18. Wang, Ling; Li, Ling-po (2013). "An effective differential harmony search algorithm for the solving non-convex economic load dispatch problems". International Journal of Electrical Power & Energy Systems. 44: 832–843. doi:10.1016/j.ijepes.2012.08.021.
19. Nekooei, Komail; Farsangi, Malihe M.; Nezamabadi-Pour, Hossein; Lee, Kwang Y. (2013). "An Improved Multi-Objective Harmony Search for Optimal Placement of DGs in Distribution Systems". IEEE Transactions on Smart Grid. 4: 557–567. doi:10.1109/TSG.2012.2237420. S2CID 12988437.
20. Hadwan, Mohammed; Ayob, Masri; Sabar, Nasser R.; Qu, Roug (2013). "A harmony search algorithm for nurse rostering problems". Information Sciences. 233: 126–140. CiteSeerX 10.1.1.298.6805. doi:10.1016/j.ins.2012.12.025.
21. Hoang, Duc Chinh; Yadav, Parikshit; Kumar, Rajesh; Panda, Sanjib Kumar (2014). "Real-Time Implementation of a Harmony Search Algorithm-Based Clustering Protocol for Energy-Efficient Wireless Sensor Networks". IEEE Transactions on Industrial Informatics. 10: 774–783. doi:10.1109/TII.2013.2273739. S2CID 3731612.
22. Ren Diao; Qiang Shen (2012). "Feature Selection with Harmony Search". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 42 (6): 1509–23. doi:10.1109/TSMCB.2012.2193613. PMID 22645272. S2CID 206794122.
23. Fattahi, Hadi; Gholami, Amin; Amiribakhtiar, Mohammad Sadegh; Moradi, Siyamak (2014). "Estimation of asphaltene precipitation from titration data: A hybrid support vector regression with harmony search". Neural Computing and Applications. 26 (4): 789. doi:10.1007/s00521-014-1766-y. S2CID 16208680.
24. "Harmony Search Algorithm".
25. Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. (2013). "A survey on applications of the harmony search algorithm". Engineering Applications of Artificial Intelligence. 26 (8): 1818. doi:10.1016/j.engappai.2013.05.008.
26. Assif Assad; Deep, Kusum (2016). "Applications of Harmony Search Algorithm in Data Mining: A Survey". Proceedings of Fifth International Conference on Soft Computing for Problem Solving. Advances in Intelligent Systems and Computing. 437. pp. 863–74. doi:10.1007/978-981-10-0451-3_77. ISBN 978-981-10-0450-6.
27. Karaboga, Dervis (2010). "Artificial bee colony algorithm". Scholarpedia. 5 (3): 6915. Bibcode:2010SchpJ...5.6915K. doi:10.4249/scholarpedia.6915.
28. Pham DT, Ghanbarzadeh A, Koc E, Otri S, Rahim S and Zaidi M. The Bees Algorithm. Technical Note, Manufacturing Engineering Centre, Cardiff University, UK, 2005.
29. Pham, D T; Castellani, M (2009). "The Bees Algorithm: Modelling foraging behaviour to solve continuous optimization problems". Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 223 (12): 2919. doi:10.1243/09544062jmes1494. S2CID 111315200.
30. Krishnanand, K.N.; Ghose, D. (2005). "Detection of multiple source locations using a glowworm metaphor with applications to collective robotics". Proceedings 2005 IEEE Swarm Intelligence Symposium, 2005. SIS 2005. pp. 84–91. doi:10.1109/SIS.2005.1501606. ISBN 978-0-7803-8916-8. S2CID 17016908.
31. Eusuff, Muzaffar; Lansey, Kevin; Pasha, Fayzul (2006). "Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization". Engineering Optimization. 38 (2): 129. doi:10.1080/03052150500384759. S2CID 18117277.
32. Chu, Shu-Chuan; Tsai, Pei-wei; Pan, Jeng-Shyang (2006). "Cat Swarm Optimization". PRICAI 2006: Trends in Artificial Intelligence. Lecture Notes in Computer Science. 4099. Guilin, China. pp. 854–858. doi:10.1007/11801603_94. ISBN 978-3-540-36667-6.
33. Atashpaz-Gargari, Esmaeil; Lucas, Caro (2007). "Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition". 2007 IEEE Congress on Evolutionary Computation. pp. 4661–7. doi:10.1109/CEC.2007.4425083. ISBN 978-1-4244-1339-3. S2CID 2736579.
34. Hosseini, Seyedmohsen; Al Khaled, Abdullah (2014). "A survey on the Imperialist Competitive Algorithm metaheuristic: Implementation in engineering domain and directions for future research". Applied Soft Computing. 24: 1078–1094. doi:10.1016/j.asoc.2014.08.024.
35. Nazari-Shirkouhi, S.; Eivazy, H.; Ghodsi, R.; Rezaie, K.; Atashpaz-Gargari, E. (2010). "Solving the integrated product mix-outsourcing problem using the Imperialist Competitive Algorithm". Expert Systems with Applications. 37 (12): 7615. doi:10.1016/j.eswa.2010.04.081.
36. Akl, Selim G.; Calude, Cristian S.; Dinneen, Michael J.; Rozenberg, Grzegorz; Todd Wareham, H. (2007). Unconventional Computation. Lecture Notes in Computer Science. 4618. arXiv:0711.2964. doi:10.1007/978-3-540-73554-0. ISBN 978-3-540-73553-3.
37. Rabanal, Pablo; Rodríguez, Ismael; Rubio, Fernando (2009). "Applying River Formation Dynamics to Solve NP-Complete Problems". Nature-Inspired Algorithms for Optimisation. Studies in Computational Intelligence. 193. pp. 333–68. doi:10.1007/978-3-642-00267-0_12. ISBN 978-3-642-00266-3.
38. Amin, Saman Hameed; Al-Raweshidy, H.S.; Abbas, Rafed Sabbar (2014). "Smart data packet ad hoc routing protocol". Computer Networks. 62: 162–181. doi:10.1016/j.bjp.2013.11.015.
39. Redlarski, Grzegorz; Pałkowski, Aleksander; Dąbkowski, Mariusz (2013). "Using River Formation Dynamics Algorithm in Mobile Robot Navigation". Solid State Phenomena. 198: 138–143. doi:10.4028/www.scientific.net/SSP.198.138. S2CID 137020536.
40. Rabanal, Pablo; Rodríguez, Ismael; Rubio, Fernando (2017). "Applications of river formation dynamics". Journal of Computational Science. 22: 26–35. doi:10.1016/j.jocs.2017.08.002.
41. Hosseini, Hamed Shah (2009). "The intelligent water drops algorithm: A nature-inspired swarm-based optimization algorithm". International Journal of Bio-Inspired Computation. 1: 71. doi:10.1504/ijbic.2009.022775.
42. Rashedi, Esmat; Nezamabadi-Pour, Hossein; Saryazdi, Saeid (2009). "GSA: A Gravitational Search Algorithm". Information Sciences. 179 (13): 2232. doi:10.1016/j.ins.2009.03.004.
43. Rashedi, Nezamabadi-pour and Saryazdi 2009
44. Hassanzadeh, Hamid Reza; Rouhani, Modjtaba (2010). "A Multi-objective Gravitational Search Algorithm". 2010 2nd International Conference on Computational Intelligence, Communication Systems and Networks. pp. 7–12. doi:10.1109/CICSyN.2010.32. ISBN 978-1-4244-7837-8.
45. Yang, Xin-She; Suash Deb (2009). "Cuckoo Search via Lévy flights". 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). pp. 210–4. doi:10.1109/NABIC.2009.5393690. ISBN 978-1-4244-5053-4. S2CID 206491725.
46. Inderscience (27 May 2010). "Cuckoo designs spring". Alphagalileo.org. Retrieved 2010-05-27.
47. Yang, Xin-She (2010). "A New Metaheuristic Bat-Inspired Algorithm". Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Studies in Computational Intelligence. 284. pp. 65–74. CiteSeerX 10.1.1.761.2708. doi:10.1007/978-3-642-12538-6_6. ISBN 978-3-642-12537-9. S2CID 14494281.
48. Tamura, Kenichi; Yasuda, Keiichiro (2016). "Spiral Optimization Algorithm Using Periodic Descent Directions". SICE Journal of Control, Measurement, and System Integration. 9 (3): 134–43. Bibcode:2016JCMSI...9..134T. doi:10.9746/jcmsi.9.134.
49. Yang, Xin-She (2012). "Flower Pollination Algorithm for Global Optimization". Unconventional Computation and Natural Computation. Lecture Notes in Computer Science. 7445. pp. 240–9. CiteSeerX 10.1.1.747.9556. doi:10.1007/978-3-642-32894-7_27. ISBN 978-3-642-32893-0. S2CID 8021636.
50. Pavlyukevich, Ilya (2007). "Lévy flights, non-local search and simulated annealing". Journal of Computational Physics. 226 (2): 1830–1844. arXiv:cond-mat/0701653. Bibcode:2007JCoPh.226.1830P. doi:10.1016/j.jcp.2007.06.008. S2CID 7368994.
51. X. S. Yang, Nature-Inspired Optimization Algorithms, Elsevier, (2014).
52. Eesa, Adel Sabry; Brifcani, Adnan Mohsin Abdulazeez; Orman, Zeynep (September 2013). "Cuttlefish Algorithm – A Novel Bio-Inspired Optimization Algorithm". International Journal of Scientific & Engineering Research. 4 (9): 1978–86.
53. Eesa, Adel Sabry; Orman, Zeynep; Brifcani, Adnan Mohsin Abdulazeez (2015). "A novel feature-selection approach based on the cuttlefish optimization algorithm for intrusion detection systems". Expert Systems with Applications. 42 (5): 2670. doi:10.1016/j.eswa.2014.11.009.
54. Tkach, I.; Edan, Y.; Jevtic, A.; Nof, S. Y. (October 2013). "Automatic Multi-sensor Task Allocation Using Modified Distributed Bees Algorithm". 2013 IEEE International Conference on Systems, Man, and Cybernetics: 1401–1406. doi:10.1109/SMC.2013.242. ISBN 978-1-4799-0652-9. S2CID 206569470.
55. Edan, Yael; Nof, Shimon Y.; Jevtić, Aleksandar; Tkach, Itshak (March 2018). "A Modified Distributed Bees Algorithm for Multi-Sensor Task Allocation". Sensors. 18 (3): 759. doi:10.3390/s18030759. PMC 5876720. PMID 29498683.
56. Baczyński Dariusz, "A new concept of an artificial ecosystem algorithm for optimization problems", CONTROL AND CYBERNETICS, 45, ISSN 0324-8569, pp. 5-36, No. 1
57. Xie, Xiao-Feng; Liu, J.; Wang, Zun-Jing (2018). "A cooperative group optimization system". Soft Computing. 18 (3): 469–495. arXiv:1808.01342. doi:10.1007/s00500-013-1069-8. S2CID 5393223.
58. Xie, Xiao-Feng; Wang, Zun-Jing (2018). "Cooperative group optimization with ants (CGO-AS): Leverage optimization with mixed individual and social learning". Applied Soft Computing. 50: 223–234. arXiv:1808.00524. doi:10.1016/j.asoc.2016.11.018. S2CID 205709082.
59. Rosenberg, Louis (February 12, 2016). "Artificial Swarm Intelligence, a Human-in-the-loop approach to A.I." Proceedings of the 13th Annual AAAI Conference on Artificial Intelligence (AAAI-16).
60. Reese, Hope (Jan 22, 2016). "How 'artificial swarm intelligence' uses people to make better predictions than experts".
61. Rosenberg, Louis B. (2015). "Human swarming, a real-time method for parallel distributed intelligence". 2015 Swarm/Human Blended Intelligence Workshop (SHBI). pp. 1–7. doi:10.1109/SHBI.2015.7321685. ISBN 978-1-4673-6522-2. S2CID 15166767.
62. CUTHBERTSON, ANTHONY (May 10, 2016). "ARTIFICIAL INTELLIGENCE TURNS $20 INTO $11,000 IN KENTUCKY DERBY BET (Newsweek)".
63. Ohlheiser, Abby (June 2, 2016). "What happened when an A.I. hive mind answered Reddit's burning politics questions (Washington Post)".
64. Kaveh, Ali; Mahdavi, Vahid Reza (2014). "Colliding bodies optimization : A novel meta-heuristic method". Computers and Structures. 139: 18–27. doi:10.1016/j.compstruc.2014.04.005.
65. Kaveh, Ali; Vazirinia, Yasin (2018). "Optimization of tower crane location and material quantity between supply and demand points: A comparative study". Periodica Polytechnica Civil Engineering. 62 (3): 732–745. doi:10.3311/PPci.11816.
66. Biyanto, Totok Ruki; Fibrianto, Henokh Yernias; Nugroho, Gunawan; Hatta, Agus Muhamad; Listijorini, Erny; Budiati, Titik; Huda, Hairul (2016). "Duelist Algorithm: An Algorithm Inspired by How Duelist Improve Their Capabilities in a Duel". Advances in Swarm Intelligence. Lecture Notes in Computer Science. 9712. pp. 39–47. arXiv:1512.00708. doi:10.1007/978-3-319-41000-5_4. ISBN 978-3-319-40999-3. S2CID 17915138.
67. Heidari, Ali Asghar; Mirjalili, Seyedali; Faris, Hossam; Aljarah, Ibrahim; Mafarja, Majdi; Chen, Huiling (2019). "Harris hawks optimization: Algorithm and applications". Future Generation Computer Systems. 97: 849–872. doi:10.1016/j.future.2019.02.028. ISSN 0167-739X.
68. Biyanto, Totok R; Matradji; Irawan, Sonny; Febrianto, Henokh Y; Afdanny, Naindar; Rahman, Ahmad H; Gunawan, Kevin S; Pratama, Januar A.D; Bethiana, Titania N (2017). "Killer Whale Algorithm: An Algorithm Inspired by the Life of Killer Whale". Procedia Computer Science. 124: 151–7. doi:10.1016/j.procs.2017.12.141.
69. Biyanto, T R; Matradji; Syamsi, M N; Fibrianto, H Y; Afdanny, N; Rahman, A H; Gunawan, K S; Pratama, J A D; Malwindasari, A; Abdillah, A I; Bethiana, T N; Putra, Y A (2017). "Optimization of Energy Efficiency and Conservation in Green Building Design Using Duelist, Killer-Whale and Rain-Water Algorithms". IOP Conference Series: Materials Science and Engineering. 267 (1): 012036. Bibcode:2017MS&E..267a2036B. doi:10.1088/1757-899X/267/1/012036.
70. Wedyan, Ahmad; Whalley, Jacqueline; Narayanan, Ajit (2017). "Hydrological Cycle Algorithm for Continuous Optimization Problems". Journal of Optimization. 2017: 1–25. doi:10.1155/2017/3828420.
71. Harifi, Sasan; Khalilian, Madjid; Mohammadzadeh, Javad; Ebrahimnejad, Sadoullah (2019). "Emperor Penguins Colony: A new metaheuristic algorithm for optimization". Evolutionary Intelligence. 12 (2): 211–226. doi:10.1007/s12065-019-00212-x. S2CID 86856463.
72. Rawal, A.; Mukhopadhyay, S. (2014). "Melt spinning of synthetic polymeric filaments". Advances in Filament Yarn Spinning of Textiles and Polymers. pp. 75–99. doi:10.1533/9780857099174.2.75. ISBN 9780857094995.
73. Zienkiewicz, O.C.; Taylor, R.L.; Fox, David (2014). "A Nonlinear Geometrically Exact Shell Model". The Finite Element Method for Solid and Structural Mechanics. pp. 519–588. doi:10.1016/B978-1-85617-634-7.00014-4. ISBN 9781856176347.
74. Wu, Yu-Shu (2016). "Multiphase Fluid and Heat Flow Coupled with Geomechanics". Multiphase Fluid Flow in Porous and Fractured Reservoirs. pp. 265–293. doi:10.1016/B978-0-12-803848-2.00011-8. ISBN 9780128038482.
75. Kaveh, Ali; Zaerreza, Ataollah (2020). "Shuffled shepherd optimization method: a new Meta-heuristic algorithm". Engineering Computations. ahead-of-print (ahead-of-print): head-of-print. doi:10.1108/EC-10-2019-0481.
76. Zervoudakis, Konstantinos; Tsafarakis, Stelios (2020). "A mayfly optimization algorithm". Computers & Industrial Engineering. ahead-of-print (ahead-of-print): head-of-print. doi:10.1016/j.cie.2020.106559.
77. Askari, Qamar; Younas, Irfan; Saeed, Mehreen (2020). "Political Optimizer: A novel socio-inspired meta-heuristic for global optimization". Knowledge-Based Systems. 195: 105709. doi:10.1016/j.knosys.2020.105709.
78. Askari, Qamar; Saeed, Mehreen; Younas, Irfan (2020). "Heap-based optimizer inspired by corporate rank hierarchy for global optimization". Expert Systems with Applications. 161: 113702. doi:10.1016/j.eswa.2020.113702.
79. Chou, Jui-Sheng; Nguyen, Ngoc-Mai (2020). "FBI inspired meta-optimization". Applied Soft Computing. 93: 106339. doi:10.1016/j.asoc.2020.106339 – via Elsevier Science Direct.
80. Chou, Jui-Sheng; Truong, Dinh-Nhat (2021). "A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean". Applied Mathematics and Computation. 389: 125535. doi:10.1016/j.amc.2020.125535 – via Elsevier Science Direct.
81. Mohammadi-Balani, Abdolkarim; Dehghan Nayeri, Mahmoud; Azar, Adel; Taghizadeh-Yazdi, Mohammadreza (2020-12-17). "Golden Eagle Optimizer: A nature-inspired metaheuristic algorithm". Computers & Industrial Engineering. 152: 107050. doi:10.1016/j.cie.2020.107050. ISSN 0360-8352.
82. "Golden Eagle Optimizer Toolbox". www.mathworks.com. Retrieved 2020-12-17.
83. Alexander Brownlee and John R. Woodward (2015). "Why we fell out of love with algorithms inspired by nature". The Conversation.
84. Jerry Swan, Steven Adriaensen, Mohamed Bishr, Edmund K. Burke, John A. Clark, Patrick De Causmaecker, Juanjo Durillo, Kevin Hammond, Emma Hart, Colin G. Johnson, Zoltan A. Kocsis, Ben Kovitz, Krzysztof Krawiec, Simon Martin, J. J. Merelo, Leandro L. Minku, Ender Özcan, Gisele L. Pappa, Erwin Pesch, Pablo Garcáa-Sánchez, Andrea Schaerf, Kevin Sim, Jim E. Smith, Thomas Stützle, Stefan Voß, Stefan Wagner, Xin Yao. "A Research Agenda for Metaheuristic Standardization". "Metaphors often inspire new metaheuristics, but without mathematical rigor, it can be hard to tell if a new metaheuristic is really distinct from a familiar one. For example, mathematically, 'Harmony search' turned out to be a simple variant of 'Evolution Strategies' even though the metaphors that inspired them were quite different. Formally describing state, representation, and operators allows genuine novelty to be distinguished from minor variation."
85. Sörensen, Kenneth (2015). "Metaheuristics-the metaphor exposed". International Transactions in Operational Research. 22: 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001.
86. Fred Glover and Kenneth Sörensen (ed.). "Metaheuristics". Scholarpedia.
87. Journal of Heuristic Policies on Heuristic Search Research. Springer.
88. "4OR – incl. Option to publish open access".

References

• Sörensen, Kenneth; Sevaux, Marc; Glover, Fred (2017-01-16). "A History of Metaheuristics" (PDF). In Martí, Rafael; Panos, Pardalos; Resende, Mauricio (eds.). Handbook of Heuristics. Springer. ISBN 978-3-319-07123-7.
• Sörensen, Kenneth (2015). "Metaheuristics-the metaphor exposed". International Transactions in Operational Research. 22: 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001.
• Lones, Michael A. (2014). "Metaheuristics in nature-inspired algorithms". Proceedings of the 2014 conference companion on Genetic and evolutionary computation companion - GECCO Comp '14. pp. 1419–22. CiteSeerX 10.1.1.699.1825. doi:10.1145/2598394.2609841. ISBN 9781450328814. S2CID 14997975.
• Fister, Iztok; Yang, Xin-She; Fister, Iztok; Brest, Janez; Fister, Dušan (2013). "A Brief Review of Nature-Inspired Algorithms for Optimization". Elektrotehniški Vestnik. arXiv:1307.4186.

External links

• Evolutionary Computation Bestiary – a tongue-in-cheek account of all the weird, even bizarre metaphor-based metaheuristics out there in the wide world of academic publishing
• The Science Matrix's List of Metaheuristic – a complete list of metaheuristic algorithms. The list can be easily filter by Name, Author or Year, and provides the link to the main publication of each algorithm.