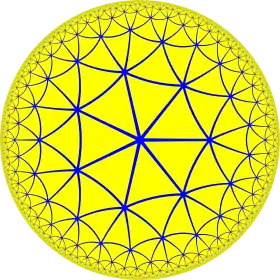
Heptagrammic-order heptagonal tiling
In geometry, the heptagrammic-order heptagonal tiling is a regular star-tiling of the hyperbolic plane. It has Schläfli symbol of {7,7/2}. The vertex figure heptagrams are {7/2}, ![]()
| Heptagrammic-order heptagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | 77/2 |
| Schläfli symbol | {7,7/2} |
| Wythoff symbol | 7 2 |
| Coxeter diagram | |
| Symmetry group | [7,3], (*732) |
| Dual | Order-7 heptagrammic tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
Related tilings
It has the same vertex arrangement as the regular order-7 triangular tiling, {3,7}. The full set of edges coincide with the edges of a heptakis heptagonal tiling.
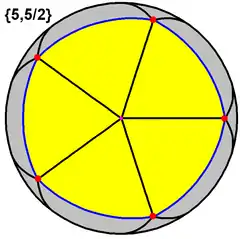
It is related to a Kepler-Poinsot polyhedron, the great dodecahedron, {5,5/2}, which is polyhedron and a density-3 regular star-tiling on the sphere (resembling a regular icosahedron in this state, similarly to this tessellation resembling the order-7 triangular tiling):
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.