Helium atom
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with either one or two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom.
 Helium-4 | |
| Names | |
|---|---|
| Systematic IUPAC name
Helium[1] | |
| Identifiers | |
3D model (JSmol) |
|
| ChEBI | |
| ChemSpider | |
| EC Number |
|
| 16294 | |
| KEGG | |
| MeSH | Helium |
PubChem CID |
|
| RTECS number |
|
| UNII | |
| UN number | 1046 |
| |
| |
| Properties | |
| He | |
| Molar mass | 4.002602 g·mol−1 |
| Appearance | Colourless gas |
| Boiling point | −269 °C (−452.20 °F; 4.15 K) |
| Thermochemistry | |
Std molar entropy (S |
126.151-126.155 J K−1 mol−1 |
| Pharmacology | |
| V03AN03 (WHO) | |
| Hazards | |
| S-phrases (outdated) | S9 |
Except where otherwise noted, data are given for materials in their standard state (at 25 °C [77 °F], 100 kPa). | |
| Infobox references | |
Introduction
The quantum mechanical description of the helium atom is of special interest, because it is the simplest multi-electron system and can be used to understand the concept of quantum entanglement. The Hamiltonian of helium, considered as a three-body system of two electrons and a nucleus and after separating out the centre-of-mass motion, can be written as
where is the reduced mass of an electron with respect to the nucleus, and are the electron-nucleus distance vectors and . The nuclear charge, is 2 for helium. In the approximation of an infinitely heavy nucleus, we have and the mass polarization term disappears. In atomic units the Hamiltonian simplifies to
It is important to note, that it operates not in normal space, but in a 6-dimensional configuration space . In this approximation (Pauli approximation) the wave function is a second order spinor with 4 components , where the indices describe the spin projection of both electrons (z-direction up or down) in some coordinate system.[2] It has to obey the usual normalization condition . This general spinor can be written as 2x2 matrix and consequently also as linear combination of any given basis of four orthogonal (in the vector-space of 2x2 matrices) constant matrices with scalar function coefficients
as . A convenient basis consists of one anti-symmetric matrix (with total spin , corresponding to a singlet state)
and three symmetric matrices (with total spin , corresponding to a triplet state)
It is easy to show, that the singlet state is invariant under all rotations (a scalar entity), while the triplet can be mapped to an ordinary space vector , with the three components
, and .
Since all spin interaction terms between the four components of in the above (scalar) Hamiltonian are neglected (e.g. an external magnetic field, or relativistic effects, like angular momentum coupling), the four Schrödinger equations can be solved independently.[3]
The spin here only comes into play through the Pauli exclusion principle, which for fermions (like electrons) requires antisymmetry under simultaneous exchange of spin and coordinates
- .
Parahelium is then the singlet state with a symmetric function and orthohelium is the triplet state with an antisymmetric function . If the electron-electron interaction term is ignored, both spatial functions can be written as linear combination of two arbitrary (orthogonal and normalized)
one-electron eigenfunctions :
or for the special cases
of (both electrons have identical quantum numbers, parahelium only): . The total energy (as eigenvalue of ) is then for all cases (independent of the symmetry).
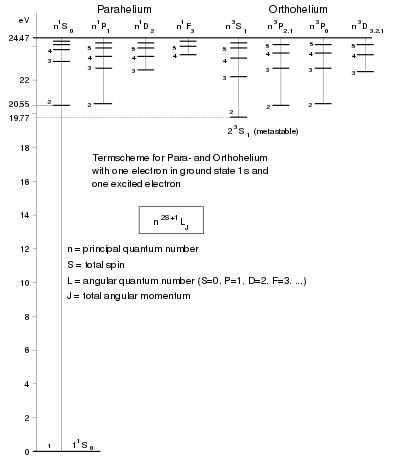
This explains the absence of the state (with ) for orthohelium, where consequently (with ) is the metastable ground state. (A state with the quantum numbers: principal quantum number , total spin , angular quantum number and total angular momentum is denoted by .)
If the electron-electron interaction term is included, the Schrödinger equation is non separable. However, also if is neglected, all states described above (even with two identical quantum numbers, like with ) cannot be written as a product of one-electron wave functions: — the wave function is entangled. One cannot say, particle 1 is in state 1 and the other in state 2, and measurements cannot be made on one particle without affecting the other.
Nevertheless, quite good theoretical descriptions of helium can be obtained within the Hartree–Fock and Thomas–Fermi approximations (see below).
The Hartree–Fock method is used for a variety of atomic systems. However it is just an approximation, and there are more accurate and efficient methods used today to solve atomic systems. The "many-body problem" for helium and other few electron systems can be solved quite accurately. For example, the ground state of helium is known to fifteen digits. In Hartree–Fock theory, the electrons are assumed to move in a potential created by the nucleus and the other electrons.
Perturbation method
The Hamiltonian for helium with two electrons can be written as a sum of the Hamiltonians for each electron:
where the zero-order unperturbed Hamiltonian is
while the perturbation term:
is the electron-electron interaction. H0 is just the sum of the two hydrogenic Hamiltonians:
where
Eni, the energy eigenvalues and , the corresponding eigenfunctions of the hydrogenic Hamiltonian will denote the normalized energy eigenvalues and the normalized eigenfunctions. So:
where
Neglecting the electron-electron repulsion term, the Schrödinger equation for the spatial part of the two-electron wave function will reduce to the 'zero-order' equation
This equation is separable and the eigenfunctions can be written in the form of single products of hydrogenic wave functions:
The corresponding energies are (in atomic units, hereafter a.u.):
Note that the wave function
An exchange of electron labels corresponds to the same energy . This particular case of degeneracy with respect to exchange of electron labels is called exchange degeneracy. The exact spatial wave functions of two-electron atoms must either be symmetric or antisymmetric with respect to the interchange of the coordinates and of the two electrons. The proper wave function then must be composed of the symmetric (+) and antisymmetric(-) linear combinations:
This comes from Slater determinants.
The factor normalizes . In order to get this wave function into a single product of one-particle wave functions, we use the fact that this is in the ground state. So . So the will vanish, in agreement with the original formulation of the Pauli exclusion principle, in which two electrons cannot be in the same state. Therefore, the wave function for helium can be written as
Where and use the wave functions for the hydrogen Hamiltonian. [lower-alpha 1] For helium, Z = 2 from
where E = −4 a.u. which is approximately −108.8 eV, which corresponds to an ionization potential V = 2 a.u. (≅54.4 eV). The experimental values are E = −2.90 a.u. (≅ −79.0 eV) and V = 0.90 a.u. (≅ 24.6 eV).
The energy that we obtained is too low because the repulsion term between the electrons was ignored, whose effect is to raise the energy levels. As Z gets bigger, our approach should yield better results, since the electron-electron repulsion term will get smaller.
So far a very crude independent-particle approximation has been used, in which the electron-electron repulsion term is completely omitted. Splitting the Hamiltonian showed below will improve the results:
where
and
V(r) is a central potential which is chosen so that the effect of the perturbation is small. The net effect of each electron on the motion of the other one is to screen somewhat the charge of the nucleus, so a simple guess for V(r) is
where S is a screening constant and the quantity Ze is the effective charge. The potential is a Coulomb interaction, so the corresponding individual electron energies are given (in a.u.) by
and the corresponding wave function is given by
If Ze was 1.70, that would make the expression above for the ground state energy agree with the experimental value E0 = −2.903 a.u. of the ground state energy of helium. Since Z = 2 in this case, the screening constant is S = 0.30. For the ground state of helium, for the average shielding approximation, the screening effect of each electron on the other one is equivalent to about of the electronic charge.[5]
The variational method
To obtain a more accurate energy the variational principle can be applied to the electron-electron potential Vee using the wave function
:
After integrating this, the result is:
This is closer to the experimental value, but if a better trial wave function is used, an even more accurate answer could be obtained. An ideal wave function would be one that doesn't ignore the influence of the other electron. In other words, each electron represents a cloud of negative charge which somewhat shields the nucleus so that the other electron actually sees an effective nuclear charge Z that is less than 2. A wave function of this type is given by:
Treating Z as a variational parameter to minimize H. The Hamiltonian using the wave function above is given by:
After calculating the expectation value of and Vee the expectation value of the Hamiltonian becomes:
The minimum value of Z needs to be calculated, so taking a derivative with respect to Z and setting the equation to 0 will give the minimum value of Z:
This shows that the other electron somewhat shields the nucleus reducing the effective charge from 2 to 1.69. So we obtain the most accurate result yet:
Where again, E1 represents the ionization energy of hydrogen.
By using more complicated/accurate wave functions, the ground state energy of helium has been calculated closer and closer to the experimental value −78.95 eV.[6] The variational approach has been refined to very high accuracy for a comprehensive regime of quantum states by G.W.F. Drake and co-workers[7][8][9] as well as J.D. Morgan III, Jonathan Baker and Robert Hill[10][11][12] using Hylleraas or Frankowski-Pekeris basis functions. One needs to include relativistic and quantum electrodynamic corrections to get full agreement with experiment to spectroscopic accuracy.[13][14]
Experimental value of ionization energy
Helium's first ionization energy is −24.587387936(25) eV.[15] This value was derived by experiment.[16] The theoretic value of Helium atom's second ionization energy is −54.41776311(2) eV.[15] The total ground state energy of the helium atom is −79.005151042(40) eV,[15] or −2.90338583(13) Atomic units a.u., which equals −5.80677166 (26) Ry.
See also
References
- For n = 1, l = 0 and m = 0, the wavefunction in a spherically symmetric potential for a hydrogen electron is .[4] In atomic units, the Bohr radius equals 1, and the wavefunction becomes .
- "Helium - PubChem Public Chemical Database". The PubChem Project. USA: National Center for Biotechnology Information.
- Rennert, P.; Schmiedel, H.; Weißmantel, C. (1988). Kleine Enzyklopädie Physik (in German). VEB Bibliographisches Institut Leipzig. pp. 192–194. ISBN 3-323-00011-0.
- Landau, L. D.; Lifschitz, E. M. (1971). Lehrbuch der Theoretischen Physik (in German). Bd. III (Quantenmechanik). Berlin: Akademie-Verlag. Kap. IX, pp. 218. OCLC 25750516.
- "Hydrogen Wavefunctions". Hyperphysics. Archived from the original on 1 February 2014.
- Bransden, B. H.; Joachain, C. J. Physics of Atoms and Molecules (2nd ed.). Pearson Education.
- Griffiths, David I. (2005). Introduction to Quantum Mechanics (Second ed.). Pearson Education.
- Drake, G.W.F.; Van, Zong-Chao (1994). "Variational eigenvalues for the S states of helium". Chemical Physics Letters. Elsevier BV. 229 (4–5): 486–490. doi:10.1016/0009-2614(94)01085-4. ISSN 0009-2614.
- Yan, Zong-Chao; Drake, G. W. F. (1995-06-12). "High Precision Calculation of Fine Structure Splittings in Helium and He-Like Ions". Physical Review Letters. American Physical Society (APS). 74 (24): 4791–4794. doi:10.1103/physrevlett.74.4791. ISSN 0031-9007. PMID 10058600.
- Drake, G. W. F. (1999). "High Precision Theory of Atomic Helium". Physica Scripta. IOP Publishing. T83 (1): 83–92. doi:10.1238/physica.topical.083a00083. ISSN 0031-8949.
- J.D. Baker, R.N. Hill, and J.D. Morgan III (1989), "High Precision Calculation of Helium Atom Energy Levels", in AIP ConferenceProceedings 189, Relativistic, Quantum Electrodynamic, and Weak Interaction Effects in Atoms (AIP, New York),123
- Baker, Jonathan D.; Freund, David E.; Hill, Robert Nyden; Morgan, John D. (1990-02-01). "Radius of convergence and analytic behavior of the 1/Z expansion". Physical Review A. American Physical Society (APS). 41 (3): 1247–1273. doi:10.1103/physreva.41.1247. ISSN 1050-2947. PMID 9903218.
- Scott, T. C.; Lüchow, A.; Bressanini, D.; Morgan, J. D. III (2007). "The Nodal Surfaces of Helium Atom Eigenfunctions" (PDF). Phys. Rev. A. 75 (6): 060101. Bibcode:2007PhRvA..75f0101S. doi:10.1103/PhysRevA.75.060101. hdl:11383/1679348.
- Drake, G. W. F.; Yan, Zong-Chao (1992-09-01). "Energies and relativistic corrections for the Rydberg states of helium: Variational results and asymptotic analysis". Physical Review A. American Physical Society (APS). 46 (5): 2378–2409. doi:10.1103/physreva.46.2378. ISSN 1050-2947. PMID 9908396.
- G.W.F. Drake (2006). "Springer Handbook of Atomic, molecular, and Optical Physics", Edited by G.W.F. Drake (Springer, New York), 199-219.
- Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team. "NIST Atomic Spectra Database Ionization Energies Data". Gaithersburg, MD: NIST.CS1 maint: uses authors parameter (link)
- D. Z. Kandula, C. Gohle, T. J. Pinkert, W. Ubachs, and K. S. E. Eikema (2010). "Extreme Ultraviolet Frequency Comb Metrology". Phys. Rev. Lett. 105 (6): 063001. arXiv:1004.5110. Bibcode:2010PhRvL.105f3001K. doi:10.1103/PhysRevLett.105.063001. PMID 20867977. S2CID 2499460.CS1 maint: uses authors parameter (link)