Epigraph (mathematics)

In mathematics, the epigraph or supergraph[1] of a function ${\displaystyle f:X\to \mathbb {R} \cup \{\pm \infty \}}$ is the set of points lying on or above its graph.[2]

A function (in black) is convex if and only if the region above its graph (in green) is a convex set. This region is the function's epigraph.

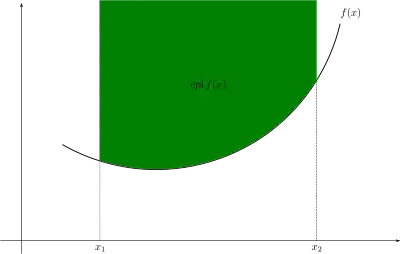
The study of continuous real-valued functions in real analysis has traditionally been closely associated with the study of their graphs, which are sets that provide geometric information (and intuition) about these functions.[2] Epigraphs serve this same purpose in the fields of convex analysis and variational analysis, in which convex functions are studied instead.[2] This is because in general, for such functions, geometric intuition is more readily obtained from a function's epigraph than from its graph.[2] The epigraph can often be used to give geometrical interpretations of the properties of convex functions or to prove these properties.

Definition

The definition of the epigraph was inspired by that of the graph of a function, where the graph of ${\displaystyle f:X\to Y}$ is defined to be the set

${\displaystyle \operatorname {graph} f:=\left\{(x,y)\in X\times Y~:~y=f(x)\right\}.}$

The epigraph or supergraph of a function ${\displaystyle f:X\to [-\infty ,\infty ]}$ valued in the extended real numbers ${\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$ is the set[2]

${\displaystyle {\begin{alignedat}{4}\operatorname {epi} f&=\left\{(x,r)\in X\times \mathbb {R} ~:~r\geq f(x)\right\}\\&=\left[f^{-1}(-\infty )\times \mathbb {R} \right]\cup \bigcup _{x\in f^{-1}(\mathbb {R} )}\{x\}\times [f(x),\infty ).\end{alignedat}}}$

Similarly, the set of points on or below the function is its hypograph. The strict epigraph is the epigraph with the graph removed:

${\displaystyle {\begin{alignedat}{4}\operatorname {epi} _{S}f&=\left\{(x,r)\in X\times \mathbb {R} ~:~r>f(x)\right\}\\&=\operatorname {epi} f\setminus \operatorname {graph} f\\&=\bigcup _{x\in X}\{x\}\times (f(x),\infty ).\end{alignedat}}}$

Despite the fact that ${\displaystyle f}$ might take one (or both) of ${\displaystyle \pm \infty }$ as a value (in which case its graph would not be a subset of ${\displaystyle X\times \mathbb {R} }$), the epigraph of ${\displaystyle f}$ is nevertheless defined to be a subset of ${\displaystyle X\times \mathbb {R} }$ rather than of ${\displaystyle X\times [-\infty ,\infty ].}$ This is intentional because when ${\displaystyle X}$ is a vector space then so is ${\displaystyle X\times \mathbb {R} }$ but ${\displaystyle X\times [-\infty ,\infty ]}$ is never a vector space.[2] The epigraph being a subset of a vector space allows for tools related to real analysis and functional analysis (and other fields) to be more readily applied.

The domain (rather than the codomain) of the function is not particularly important for this definition; it can be any linear space[1] or even an arbitrary set[3] instead of ${\displaystyle \mathbb {R} ^{n}}$.

Properties

The epigraph of a function ${\displaystyle f:X\to [-\infty ,\infty ]}$ is related to its graph and strict epigraph by

${\displaystyle \,\operatorname {epi} f\,\subseteq \,\operatorname {epi} _{S}f\,\cup \,\operatorname {graph} f}$

where set equality holds if and only if ${\displaystyle f}$ is real-valued. However,

${\displaystyle \operatorname {epi} f=\left[\operatorname {epi} _{S}f\,\cup \,\operatorname {graph} f\right]\,\cap \,\left[X\times \mathbb {R} \right]}$

always holds. The epigraph is empty if and only if the function is identically equal to infinity.

Just as any function can be reconstructed from its graph, so too can any extended real-valued function ${\displaystyle f}$ on ${\displaystyle X}$ be reconstructed from its epigraph ${\displaystyle E:=\operatorname {epi} f}$ (even when ${\displaystyle f}$ takes on ${\displaystyle \pm \infty }$ as a value). Given ${\displaystyle x\in X,}$ if ${\displaystyle E\cap \left(\{x\}\times \mathbb {R} \right)=\varnothing }$ then ${\displaystyle f(x)=\infty ,}$ while if ${\displaystyle E\cap \left(\{x\}\times \mathbb {R} \right)=\{x\}\times \mathbb {R} }$ then ${\displaystyle f(x)=-\infty ,}$ and otherwise ${\displaystyle E\cap \left(\{x\}\times \mathbb {R} \right)}$ is necessarily of the form ${\displaystyle \{x\}\times [f(x),\infty ),}$ from which the value of ${\displaystyle f(x)}$ can be obtained by taking the infimum of the interval. Specifically, for any ${\displaystyle x\in X,}$

${\displaystyle f(x)=\inf _{}\{r\in \mathbb {R} ~:~(x,r)\in E\}}$

where by definition, ${\displaystyle \inf _{}\varnothing$ :=\infty .} This same formula can also be used to reconstruct ${\displaystyle f}$ from its strict epigraph ${\displaystyle E:=\operatorname {epi} _{S}f.}$

A function is convex if and only if its epigraph is a convex set. The epigraph of a real affine function ${\displaystyle g:\mathbb {R} ^{n}\to \mathbb {R} }$ is a halfspace in ${\displaystyle \mathbb {R} ^{n+1}.}$

A function is lower semicontinuous if and only if its epigraph is closed.

See also

• Effective domain
• Hypograph (mathematics)
• Proper convex function

Citations

1. Pekka Neittaanmäki; Sergey R. Repin (2004). Reliable Methods for Computer Simulation: Error Control and Posteriori Estimates. Elsevier. p. 81. ISBN 978-0-08-054050-4.
2. Rockafellar & Wets 2009, pp. 1-37. sfn error: no target: CITEREFRockafellarWets2009 (help)
3. Charalambos D. Aliprantis; Kim C. Border (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3rd ed.). Springer Science & Business Media. p. 8. ISBN 978-3-540-32696-0.

References

• Rockafellar, R. Tyrrell; Wets, Roger J.-B. (26 June 2009). Variational Analysis. Grundlehren der mathematischen Wissenschaften. 317. Berlin New York: Springer Science & Business Media. ISBN 9783642024313. OCLC 883392544.CS1 maint: date and year (link)
• Rockafellar, Ralph Tyrell (1996), Convex Analysis, Princeton University Press, Princeton, NJ. ISBN 0-691-01586-4.