Enneagonal antiprism
In geometry, the enneagonal antiprism (or nonagonal antiprism) is one in an infinite set of convex antiprisms formed by triangle sides and two regular polygon caps, in this case two enneagons.
| Uniform enneagonal antiprism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 20, E = 36 V = 18 (χ = 2) |
| Faces by sides | 18{3}+2{9} |
| Schläfli symbol | s{2,18} sr{2,9} |
| Wythoff symbol | | 2 2 9 |
| Coxeter diagram | |
| Symmetry group | D9d, [2+,18], (2*9), order 36 |
| Rotation group | D9, [9,2]+, (922), order 18 |
| References | U77(g) |
| Dual | Enneagonal trapezohedron |
| Properties | convex |
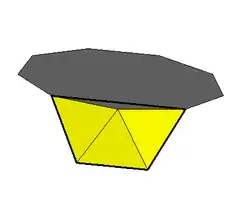 Vertex figure 3.3.3.9 | |
Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.
In the case of a regular 9-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.
If faces are all regular, it is a semiregular polyhedron.
See also
| Family of uniform n-gonal antiprisms | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | ... | Apeirogonal antiprism | ||||||||||||
| Spherical tiling image | Plane tiling image | |||||||||||||
| Vertex configuration n.3.3.3 | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 | |
External links
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model
- Conway Notation for Polyhedra Try: "A9"
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.