Darboux integral

In real analysis, a branch of mathematics, the Darboux integral is constructed using Darboux sums and is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal.[1] The definition of the Darboux integral has the advantage of being easier to apply in computations or proofs than that of the Riemann integral. Consequently, introductory textbooks on calculus and real analysis often develop Riemann integration using the Darboux integral, rather than the true Riemann integral.[2] Moreover, the definition is readily extended to defining Riemann–Stieltjes integration.[3] Darboux integrals are named after their inventor, Gaston Darboux.

Definition

The definition of the Darboux integral considers upper and lower (Darboux) integrals, which exist for any bounded real-valued function f on the interval [a, b]. The Darboux integral exists if and only if the upper and lower integrals are equal. The upper and lower integrals are in turn the infimum and supremum, respectively, of upper and lower (Darboux) sums which over- and underestimate, respectively, the "area under the curve." In particular, for a given partition of the interval of integration, the upper and lower sums add together the areas of rectangular slices whose heights are the supremum and infimum, respectively, of f in each subinterval of the partition. These ideas are made precise below:

Darboux sums

A partition of an interval [a, b] is a finite sequence of values x_i such that

${\displaystyle a=x_{0}<x_{1}<\cdots <x_{n}=b.\,\!}$

Each interval [x_i−1, x_i] is called a subinterval of the partition. Let ƒ: [a, b] → ℝ be a bounded function, and let

${\displaystyle P=(x_{0},\ldots ,x_{n})\,\!}$

be a partition of [a, b]. Let

${\displaystyle {\begin{aligned}M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x),\\m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x).\end{aligned}}}$

Lower (green) and upper (green plus lavender) Darboux sums for four subintervals

The upper Darboux sum of ƒ with respect to P is

${\displaystyle U_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})M_{i}.\,\!}$

The lower Darboux sum of ƒ with respect to P is

${\displaystyle L_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})m_{i}.\,\!}$

The lower and upper Darboux sums are often called the lower and upper sums.

Darboux integrals

The upper Darboux integral of ƒ is

${\displaystyle U_{f}=\inf\{U_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}$

The lower Darboux integral of ƒ is

${\displaystyle L_{f}=\sup\{L_{f,P}\colon P{\text{ is a partition of }}[a,b]\}.\,\!}$

In some literature an integral symbol with an underline and overline represent the lower and upper Darboux integrals respectively.

${\displaystyle {\begin{aligned}L_{f}\equiv {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x&\quad U_{f}\equiv {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\end{aligned}},}$

and like Darboux sums they are sometimes simply called the lower and upper integrals.

If U_ƒ = L_ƒ, then we call the common value the Darboux Integral.[4] We also say that ƒ is Darboux-integrable or simply integrable and set

${\displaystyle \int _{a}^{b}{f(t)\,dt}=U_{f}=L_{f},\,\!}$

An equivalent and sometimes useful criterion for the integrability of f is to show that for every ε > 0 there exists a partition P_ε of [a, b] such that[5]

${\displaystyle U_{f,P_{\epsilon }}-L_{f,P_{\epsilon }}<\varepsilon .}$

Properties

• For any given partition, the upper Darboux sum is always greater than or equal to the lower Darboux sum. Furthermore, the lower Darboux sum is bounded below by the rectangle of width (b−a) and height inf(f) taken over [a, b]. Likewise, the upper sum is bounded above by the rectangle of width (b−a) and height sup(f).

${\displaystyle (b-a)\inf _{x\in [a,b]}f(x)\leqslant L_{f,P}\leqslant U_{f,P}\leqslant (b-a)\sup _{x\in [a,b]}f(x)}$

• The lower and upper Darboux integrals satisfy

${\displaystyle {\underline {\int _{a}^{b}}}f(x)\,dx\leqslant {\overline {\int _{a}^{b}}}f(x)\,dx}$

• Given any c in (a, b)

${\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx&={\underline {\int _{a}^{c}}}f(x)\,dx+{\underline {\int _{c}^{b}}}f(x)\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx&={\overline {\int _{a}^{c}}}f(x)\,dx+{\overline {\int _{c}^{b}}}f(x)\,dx\end{aligned}}}$

• The lower and upper Darboux integrals are not necessarily linear. Suppose that g:[a, b] → ℝ is also a bounded function, then the upper and lower integrals satisfy the following inequalities.

${\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,dx+{\underline {\int _{a}^{b}}}g(x)\,dx&\leqslant {\underline {\int _{a}^{b}}}(f(x)+g(x))\,dx\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,dx+{\overline {\int _{a}^{b}}}g(x)\,dx&\geqslant {\overline {\int _{a}^{b}}}(f(x)+g(x))\,dx\end{aligned}}}$

• For a constant c ≥ 0 we have

${\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\end{aligned}}}$

• For a constant c ≤ 0 we have

${\displaystyle {\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\end{aligned}}}$

• Consider the function:

${\displaystyle {\begin{cases}F:[a,b]\to \mathbb {R} \\F(x)={\underline {\int _{a}^{x}}}f(t)\,dt\end{cases}}}$

then F is Lipschitz continuous. An identical result holds if F is defined using an upper Darboux integral.

Examples

A Darboux-integrable function

Suppose we want to show that the function f(x) = x is Darboux-integrable on the interval [0, 1] and determine its value. To do this we partition [0, 1] into n equally sized subintervals each of length 1/n. We denote a partition of n equally sized subintervals as P_n.

Now since f(x) = x is strictly increasing on [0, 1], the infimum on any particular subinterval is given by its starting point. Likewise the supremum on any particular subinterval is given by its end point. The starting point of the kth subinterval in P_n is (k−1)/n and the end point is k/n. Thus the lower Darboux sum on a partition P_n is given by

${\displaystyle {\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k-1}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}[k-1]\\&={\frac {1}{n^{2}}}\left[{\frac {(n-1)n}{2}}\right]\end{aligned}}}$

similarly, the upper Darboux sum is given by

${\displaystyle {\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}k\\&={\frac {1}{n^{2}}}\left[{\frac {(n+1)n}{2}}\right]\end{aligned}}}$

Since

${\displaystyle {\begin{aligned}U_{f,P_{n}}-L_{f,P_{n}}&={\frac {1}{n}}\end{aligned}}}$

Thus for given any ε > 0, we have that any partition P_n with n > 1/ε satisfies

${\displaystyle {\begin{aligned}U_{f,P_{n}}-L_{f,P_{n}}&<\epsilon \end{aligned}}}$

which shows that f is Darboux integrable. To find the value of the integral note that

${\displaystyle {\begin{aligned}\int _{0}^{1}f(x)\,dx&=\lim _{n\to \infty }U_{f,P_{n}}=\lim _{n\to \infty }L_{f,P_{n}}={\frac {1}{2}}\end{aligned}}}$

Darboux sums

Darboux upper sums of the function y = x²

Darboux lower sums of the function y = x²

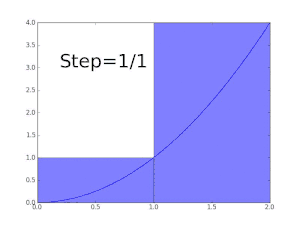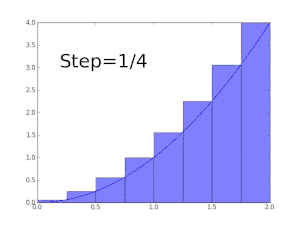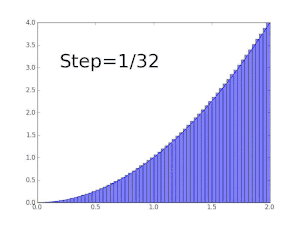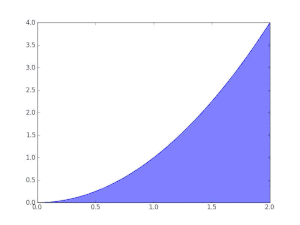
An unintegrable function

Suppose we have the function f: [0, 1] → ℝ defined as

${\displaystyle {\begin{aligned}f(x)&={\begin{cases}0,&{\text{if }}x{\text{ is rational}}\\1,&{\text{if }}x{\text{ is irrational}}\end{cases}}\end{aligned}}}$

Since the rational and irrational numbers are both dense subsets of ℝ, it follows that f takes on the value of 0 and 1 on every subinterval of any partition. Thus for any partition P we have

${\displaystyle {\begin{aligned}L_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}f=0\\U_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}f=1\end{aligned}}}$

from which we can see that the lower and upper Darboux integrals are unequal.

Refinement of a partition and relation to Riemann integration

When passing to a refinement, the lower sum increases and the upper sum decreases.

A refinement of the partition ${\displaystyle x_{0},\ldots ,x_{n}\,\!}$ is a partition ${\displaystyle y_{0},\ldots ,y_{m}\,\!}$ such that for all i = 0, ..., n there is an integer r(i) such that

${\displaystyle x_{i}=y_{r(i)}.\,\!}$

In other words, to make a refinement, cut the subintervals into smaller pieces and do not remove any existing cuts.

If ${\displaystyle P'=(y_{0},\ldots ,y_{m})\,\!}$ is a refinement of ${\displaystyle P=(x_{0},\ldots ,x_{n}),\,\!}$ then

${\displaystyle U_{f,P}\geq U_{f,P'}\,\!}$

and

${\displaystyle L_{f,P}\leq L_{f,P'}.\,\!}$

If P₁, P₂ are two partitions of the same interval (one need not be a refinement of the other), then

${\displaystyle L_{f,P_{1}}\leq U_{f,P_{2}},\,\!}$

and it follows that

${\displaystyle L_{f}\leq U_{f}.\,\!}$

Riemann sums always lie between the corresponding lower and upper Darboux sums. Formally, if ${\displaystyle P=(x_{0},\ldots ,x_{n})\,\!}$ and ${\displaystyle T=(t_{1},\ldots ,t_{n})\,\!}$ together make a tagged partition

${\displaystyle x_{0}\leq t_{1}\leq x_{1}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}\,\!}$

(as in the definition of the Riemann integral), and if the Riemann sum of ƒ corresponding to P and T is R, then

${\displaystyle L_{f,P}\leq R\leq U_{f,P}.\,\!}$

From the previous fact, Riemann integrals are at least as strong as Darboux integrals: if the Darboux integral exists, then the upper and lower Darboux sums corresponding to a sufficiently fine partition will be close to the value of the integral, so any Riemann sum over the same partition will also be close to the value of the integral. There is a tagged partition that comes arbitrarily close to the value of the upper Darboux integral or lower Darboux integral, and consequently, if the Riemann integral exists, then the Darboux integral must exist as well.

See also

• Regulated integral
• Lebesgue integration
• Minimum bounding rectangle

Notes

1. David J. Foulis; Mustafa A. Munem (1989). After Calculus: Analysis. Dellen Publishing Company. p. 396. ISBN 978-0-02-339130-9.
2. Spivak, M. (1994). Calculus (3rd. edition). Houston, TX: Publish Or Perish, Inc. pp. 253–255. ISBN 0-914098-89-6.
3. Rudin, W. (1976). Principles of Mathematical Analysis (3rd. edition). New York: McGraw-Hill. pp. 120–122. ISBN 007054235X.
4. Wolfram MathWorld
5. Spivak 2008, chapter 13.

References

• "Darboux Integral". Wolfram MathWorld. Retrieved 2013-01-08.
• Darboux integral at Encyclopaedia of Mathematics
• "Darboux sum", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Spivak, Michael (2008), Calculus (4 ed.), Publish or Perish, ISBN 978-0914098911
• "Equivalence of Darboux nd Riemann integral".