Wigner–Seitz cell

The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in solid-state physics.

Wigner–Seitz primitive cell for different angle parallelogram lattices.

The unique property of a crystal is that its atoms are arranged in a regular three-dimensional array called a lattice. All the properties attributed to crystalline materials stem from this highly ordered structure. Such a structure exhibits discrete translational symmetry. In order to model and study such a periodic system, one needs a mathematical "handle" to describe the symmetry and hence draw conclusions about the material properties consequent to this symmetry. The Wigner–Seitz cell is a means to achieve this.

A Wigner–Seitz cell is an example of a primitive cell, which is a unit cell containing exactly one lattice point. For any given lattice, there are an infinite number of possible primitive cells. However there is only one Wigner–Seitz cell for any given lattice. It is the locus of points in space that are closer to that lattice point than to any of the other lattice points.

A Wigner–Seitz cell, like any primitive cell, is a fundamental domain for the discrete translation symmetry of the lattice. The primitive cell of the reciprocal lattice in momentum space is called the Brillouin zone.

Overview

Background

The concept of voronoi decomposition was investigated by Peter Gustav Lejeune Dirichlet, leading to the name Dirichlet domain. Further contributions were made from Evgraf Fedorov, (Fedorov parallelohedron), Georgy Voronoy (Voronoi polyhedron),[1][2] and Paul Niggli (Wirkungsbereich).[3]

The application to condensed matter physics was first proposed by Eugene Wigner and Frederick Seitz in a 1933 paper, where it was used to solve the Schrödinger equation for free electrons in elemental sodium.[4] They approximated the shape of the Wigner–Seitz cell in sodium, which is a truncated octahedron, as a sphere of equal volume, and solved the Schrödinger equation exactly using periodic boundary conditions, which require ${\displaystyle d\psi /dr=0}$ at the surface of the sphere. A similar calculation which also accounted for the non-spherical nature of the Wigner–Seitz cell was performed later by John C. Slater.[5]

There are only five topologically distinct polyhedra which tile three-dimensional space, ℝ³. These are referred to as the parallelohedra. They are the subject of mathematical interest, such as in higher dimensions.[6] These five paralellohedra can be used to classify the three dimensional lattices using the concept of a projective plane, as suggested by John Horton Conway and Neil Sloane.[7] However, while a topological classification considers any affine transformation to lead to an identical class, a more specific classification leads to 24 distinct classes of voronoi polyhedra with parallel edges which tile space.[3] For example, the rectangular cuboid, right square prism, and cube belong to the same topological class, but are distinguished by different ratios of their sides. This classification of the 24 types of voronoi polyhedra for Bravais lattices was first laid out by Boris Delaunay.[8]

Definition

The Wigner–Seitz cell around a lattice point is defined as the locus of points in space that are closer to that lattice point than to any of the other lattice points.[9]

It can be shown mathematically that a Wigner–Seitz cell is a primitive cell. This implies that the cell spans the entire direct space without leaving any gaps or holes, a property known as tessellation.

Constructing the cell

Construction of a Wigner–Seitz primitive cell.

The general mathematical concept embodied in a Wigner–Seitz cell is more commonly called a Voronoi cell, and the partition of the plane into these cells for a given set of point sites is known as a Voronoi diagram.

The construction process for the Wigner-Seitz cell of a hexagonal lattice.

The cell may be chosen by first picking a lattice point. After a point is chosen, lines are drawn to all nearby lattice points. At the midpoint of each line, another line is drawn normal to each of the first set of lines.

In the case of a three-dimensional lattice, a perpendicular plane is drawn at the midpoint of the lines between the lattice points. By using this method, the smallest area (or volume) is enclosed in this way and is called the Wigner–Seitz primitive cell. All area (or space) within the lattice will be filled by this type of primitive cell and will leave no gaps.

Nearby lattice points are continually examined until the area or volume enclosed is the correct area or volume for a primitive cell. Alternatively, if the basis vectors of the lattice are reduced using lattice reduction only a set number of lattice points need to be used.[10] In two-dimensions only the lattice points that make up the 4 unit cells that share a vertex with the origin need to be used. In three-dimensions only the lattice points that make up the 8 unit cells that share a vertex with the origin need to be used.

The Wigner-Seitz cell of the primitive cubic lattice is a cube. In mathematics, it is known as the cubic honeycomb.

The Wigner–Seitz cell of the body-centered cubic lattice is a truncated octahedron.[9] In mathematics, it is known as the bitruncated cubic honeycomb.

The Wigner–Seitz cell of the face-centered cubic lattice is a rhombic dodecahedron.[9] In mathematics, it is known as the rhombic dodecahedral honeycomb.

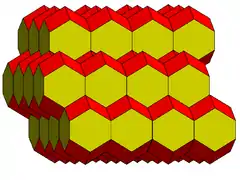The Wigner–Seitz cell of the body-centered tetragonal lattice that has lattice constants with ${\displaystyle c/a>{\sqrt {2}}}$ is the elongated dodecahedron.

The Wigner–Seitz cell of the primitive hexagonal lattice is the hexagonal prism. In mathematics, it is known as the hexagonal prismatic honeycomb.

The shape of the Wigner–Seitz cell for any Bravais lattice takes the form of one of the 24 Voronoi polyhedra.[3][11] For specifying additional constraints, ${\displaystyle a,b,c,\alpha ,\beta }$ are the unit cell parameters, and ${\displaystyle {\vec {a}}_{1},{\vec {a}}_{2},{\vec {a}}_{3},{\vec {a}}_{4}}$ are the basis vectors.

		Topological class (the affine equivalent parallelohedron)
		Truncated octahedron	Elongated dodecahedron	Rhombic dodecahedron	Hexagonal prism	Cube
Bravais lattice	Primitive cubic					Any
	Face-centered cubic			Any
	Body-centered cubic	Any
	Primitive hexagonal				Any
	Primitive rhombohedral	${\displaystyle \alpha >90^{\circ }}$		${\displaystyle \alpha <90^{\circ }}$
	Primitive tetragonal					Any
	Body-centered tetragonal	${\displaystyle c/a<{\sqrt {2}}}$	${\displaystyle c/a>{\sqrt {2}}}$
	Primitive orthorhombic					Any
	Base-centered orthorhombic				Any
	Face-centered orthorhombic	Any
	Body-centered orthorhombic	${\displaystyle c^{2}<a^{2}+b^{2}}$	${\displaystyle c^{2}>a^{2}+b^{2}}$	${\displaystyle c^{2}=a^{2}+b^{2}}$
	Primitive monoclinic				Any
	Base-centered monoclinic	${\displaystyle a<b}$	${\displaystyle a>b}$, ${\displaystyle a^{2}-b^{2}>2ac\cos {\beta }}$	${\displaystyle a>b}$, ${\displaystyle a^{2}-b^{2}=2ac\cos {\beta }}$
		${\displaystyle a>b}$, ${\displaystyle a^{2}-b^{2}<2ac\cos {\beta }}$	${\displaystyle a=b}$
	Primitive triclinic	${\displaystyle {\vec {a}}_{i}\cdot {\vec {a}}_{j}\neq 0}$ ${\displaystyle i,j\in \{1,2,3,4\}}$ where ${\displaystyle i\neq j}$	${\displaystyle {\vec {a}}_{i}\cdot {\vec {a}}_{j}=0}$ one time	${\displaystyle {\vec {a}}_{i}\cdot {\vec {a}}_{j}=0={\vec {a}}_{k}\cdot {\vec {a}}_{l}}$ ${\displaystyle i,j,k,l\in \{1,2,3,4\}}$ where ${\displaystyle i\neq j\neq k\neq l}$

Composite lattices

For composite lattices, (crystals which have more than one vector in their basis) each single lattice point represents multiple atoms. We can break apart each Wigner–Seitz cell into subcells by further Voronoi decomposition according to the closest atom, instead of the closest lattice point.[12] For example, the diamond crystal structure contains a two atom basis. In diamond, carbon atoms have tetraheral sp³ bonding, but since tetrahedra do not tile space, the voronoi decomposition of the diamond crystal structure is actually the triakis truncated tetrahedral honeycomb.[13] Another example is applying Voronoi decomposition to the atoms in the A15 phases, which forms the polyhedral approximation of the Weaire–Phelan structure.

Symmetry

The Wigner–Seitz cell always has the same point symmetry as the underlying Bravais lattice.[9] For example, the cube, truncated octahedron, and rhombic dodecahedron have point symmetry O_h, since the respetive Bravais lattices used to generate them all belong to the cubic lattice system, which has O_h point symmetry.

Brillouin zone

In practice, the Wigner–Seitz cell itself is actually rarely used as a description of direct space, where the conventional unit cells are usually used instead. However, the same decomposition is extremely important when applied to reciprocal space. The Wigner–Seitz cell in the reciprocal space is called the Brillouin zone, which contains the information about whether a material will be a conductor, semiconductor or an insulator.

See also

• Delaunay triangulation
• Coordination geometry
• Crystal field theory

References

1. Voronoi, Georges (1908-07-01). "Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs". Journal für die reine und angewandte Mathematik (Crelles Journal) (in French). Walter de Gruyter GmbH. 1908 (134): 198–287. doi:10.1515/crll.1908.134.198. ISSN 0075-4102.
2. Voronoi, Georges (1909-07-01). "Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième Mémoire. Recherches sur les paralléloèdres primitifs". Journal für die reine und angewandte Mathematik (Crelles Journal) (in French). Walter de Gruyter GmbH. 1909 (136): 67–182. doi:10.1515/crll.1909.136.67. ISSN 0075-4102.
3. Bohm, J.; Heimann, R. B.; Bohm, M. (1996). "Voronoi Polyhedra: A Useful Tool to Determine the Symmetry and Bravais Class of Crystal Lattices". Crystal Research and Technology. Wiley. 31 (8): 1069–1075. doi:10.1002/crat.2170310816. ISSN 0232-1300.
4. E. Wigner; F. Seitz (15 May 1933). "On the Constitution of Metallic Sodium". Physical Review. 43 (10): 804. doi:10.1103/PhysRev.43.804.
5. Slater, J. C. (1934-06-01). "Electronic Energy Bands in Metals". Physical Review. American Physical Society (APS). 45 (11): 794–801. doi:10.1103/physrev.45.794. ISSN 0031-899X.
6. Garber, A. I. (2012). "Belt distance between facets of space-filling zonotopes". Mathematical Notes. Pleiades Publishing Ltd. 92 (3–4): 345–355. arXiv:1010.1698. doi:10.1134/s0001434612090064. ISSN 0001-4346.
7. Austin, Dave (2011). "Fedorov's Five Parallelohedra". American Mathematical Society. Archived from the original on 2019-01-03.
8. Delone, B. N.; Galiulin, R. V.; Shtogrin, M. I. (1975). "On the Bravais types of lattices". Journal of Soviet Mathematics. Springer Science and Business Media LLC. 4 (1): 79–156. doi:10.1007/bf01084661. ISSN 0090-4104.
9. Neil W. Ashcroft; N. David Mermin (1976). Solid State Physics. p. 73–75. ISBN 978-0030839931.
10. Hart, Gus L W; Jorgensen, Jeremy J; Morgan, Wiley S; Forcade, Rodney W (2019-06-26). "A robust algorithm for k-point grid generation and symmetry reduction". Journal of Physics Communications. 3 (6): 065009. doi:10.1088/2399-6528/ab2937. ISSN 2399-6528.
11. Lulek, T; Florek, W; Wałcerz, S (1995). "Bravais classes, Vonoroï cells, Delone symbols". Symmetry and Structural Properties of Condensed Matter (PDF). World Scientific. pp. 279–316. doi:10.1142/9789814533508. ISBN 978-981-02-2059-4.
12. Giuseppe Grosso; Giuseppe Pastori Parravicini (2000-03-20). Solid State Physics. p. 54. ISBN 978-0123044600.
13. Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. p. 332. ISBN 978-1568812205.