Walter Trump

Walter Trump is a German mathematician. He is known for his work in recreational mathematics.

He has made contributions working on both the square packing problem and the magic tile problem. In 1979 he discovered the optimal known packing of 11 equal squares in a larger square,[1] and in 2003, along with Christian Boyer, developed the first known magic cube of order 5.[2] In 2009, he pioneered work on water retention on mathematical surfaces.

Until he retired in 2016, Trump worked as a teacher for mathematics and physics at the Gymnasium in Stein, Bavaria.

Magic squares

In 2010, Trump placed first in Al Zimmermann's programming contest which asked contestants to find the maximum water retention for magic squares orders 4–28.[3] This specific work found a more general application in statistical physics with the resulting 2012 Physical Review Letters "Retention Capacity of Random Surfaces", which he coauthored.[4] In 2014, he and Francis Gaspalou were able to calculate all 8x8 bimagic squares.[5]

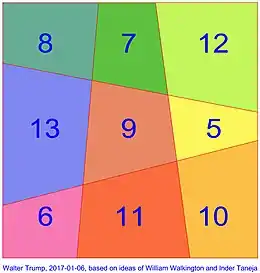
In January 2017, building on ideas of William Walkington and Inder Taneja, Trump discovered the world's first linear area magic square (shown at right).[6]

References
  1. Konhauser, Joseph D. E.; Daniel J. Velleman; S. Wagon (1996). Which way did the bicycle go?: and other intriguing mathematical mysteries. Cambridge University Press. p. 105. ISBN 978-0-88385-325-2.
  2. Niederman, Derrick (2009). Number freak: from 1 to 200— the hidden language of numbers revealed. Penguin. p. 63. ISBN 978-0-399-53459-1.
  3. Retaining Water Al Zimmermann's Programming Contests: closed June 12, 2010
  4. Knecht, Craig; Walter Trump; Daniel ben-Avraham; Robert M. Ziff (2012). "Retention capacity of random surfaces". Physical Review Letters. 108 (4): 045703. arXiv:1110.6166. Bibcode:2012PhRvL.108d5703K. doi:10.1103/PhysRevLett.108.045703. PMID 22400865.
  5. Notes on Magic Squares and Cubes by Walter Trump
  6. Science & Math: Area Magic Squares Futility Closet, January 19, 2017


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.