Vojtěch Jarník

Vojtěch Jarník (Czech pronunciation: [ˈvojcɛx ˈjarɲiːk]; 1897–1970) was a Czech mathematician who worked for many years as a professor and administrator at Charles University, and helped found the Czechoslovak Academy of Sciences. He is the namesake of Jarník's algorithm for minimum spanning trees.

Vojtěch Jarník
Born(1897-12-22)December 22, 1897
Prague, Bohemia, Austrian Empire
DiedSeptember 22, 1970(1970-09-22) (aged 72)
Prague, Czechoslovakia
NationalityCzechoslovakia
Known for
Scientific career
FieldsMathematics
InstitutionsCharles University
Doctoral advisorKarel Petr
Other academic advisorsEdmund Landau
Doctoral students

Jarník worked in number theory, mathematical analysis, and graph algorithms. He has been called "probably the first Czechoslovak mathematician whose scientific works received wide and lasting international response".[1] As well as developing Jarník's algorithm, he found tight bounds on the number of lattice points on convex curves, studied the relationship between the Hausdorff dimension of sets of real numbers and how well they can be approximated by rational numbers, and investigated the properties of nowhere-differentiable functions.

Education and career

Jarník was born December 22, 1897. He was the son of Jan Urban Jarník, a professor of Romance language philology at Charles University,[2] and his older brother, Hertvík Jarník, also became a professor of linguistics.[3] Despite this background, Jarník learned no Latin at his gymnasium (the C.K. české vyšší reálné gymnasium, Ječná, Prague), so when he entered Charles University in 1915 he had to do so as an extraordinary student until he could pass a Latin examination three semesters later.[3]

He studied mathematics and physics at Charles University from 1915 to 1919, with Karel Petr as a mentor. After completing his studies, he became an assistant to Jan Vojtěch at the Brno University of Technology, where he also met Mathias Lerch.[3] In 1921 he completed a doctoral degree (RNDr.) at Charles University with a dissertation on Bessel functions supervised by Petr,[3] then returned to Charles University as Petr's assistant.[3][1][4]

While keeping his position at Charles University, he studied with Edmund Landau at the University of Göttingen from 1923 to 1925 and again from 1927 to 1929.[5] On his first return to Charles University he defended his habilitation,[1] and on his return from the second visit, he was given a chair in mathematics as an extraordinary professor.[1][4] He was promoted to full professor in 1935 and later served as Dean of Sciences (1947–1948) and Vice-Rector (1950–1953).[1] He retired in 1968.[1][4]

Jarník supervised the dissertations of 16 doctoral students. Notable among these are Miroslav Katětov, a chess master who became rector of Charles University, Jaroslav Kurzweil, known for the Henstock–Kurzweil integral, and Slovak mathematician Tibor Šalát.[3][6]

He died September 22, 1970.[1]

Contributions

Although Jarník's 1921 dissertation,[1] like some of his later publications, was in mathematical analysis, his main area of work was in number theory. He studied the Gauss circle problem and proved a number of results on Diophantine approximation, lattice point problems, and the geometry of numbers.[4] He also made pioneering, but long-neglected, contributions to combinatorial optimization.[7]

Number theory
A convex curve through 13 integer lattice points

The Gauss circle problem asks for the number of points of the integer lattice enclosed by a given circle. One of Jarník's theorems (1926), related to this problem, is that any convex curve with length L passes through at most

points of the integer lattice. The in this formula is an instance of Big O notation. Neither the exponent of L nor the leading constant of this bound can be improved, as there exist convex curves with this many grid points.[8][9]

Another theorem of Jarník in this area shows that, for any closed convex curve in the plane with a well-defined length, the absolute difference between the area it encloses and the number of integer points it encloses is at most its length.[10]

Jarník also published several results in Diophantine approximation, the study of the approximation of real numbers by rational numbers. He proved (1928–1929) that the badly approximable real numbers (the ones with bounded terms in their continued fractions) have Hausdorff dimension one. This is the same dimension as the set of all real numbers, intuitively suggesting that the set of badly approximable numbers is large. He also considered the numbers x for which there exist infinitely many good rational approximations p/q, with

for a given exponent k > 2, and proved (1929) that these have the smaller Hausdorff dimension 2/k. The second of these results was later rediscovered by Besicovitch.[11] Besicovitch used different methods than Jarník to prove it, and the result has come to be known as the Jarník–Besicovitch theorem.[12]

Mathematical analysis

Jarník's work in real analysis was sparked by finding, in the unpublished works of Bernard Bolzano, a definition of a continuous function that was nowhere differentiable. Bolzano's 1830 discovery predated the 1872 publication of the Weierstrass function, previously considered to be the first example of such a function. Based on his study of Bolzano's function, Jarník was led to a more general theorem: If a real-valued function of a closed interval does not have bounded variation in any subinterval, then there is a dense subset of its domain on which at least one of its Dini derivatives is infinite. This applies in particular to the nowhere-differentiable functions, as they must have unbounded variation in all intervals. Later, after learning of a result by Stefan Banach and Stefan Mazurkiewicz that generic functions (that is, the members of a residual set of functions) are nowhere differentiable, Jarník proved that at almost all points, all four Dini derivatives of such a function are infinite. Much of his later work in this area concerned extensions of these results to approximate derivatives.[13]

Combinatorial optimization
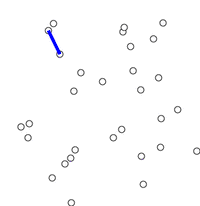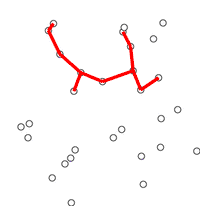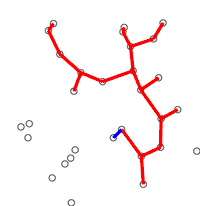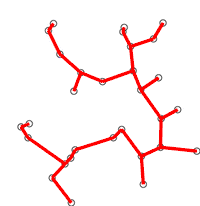
Animation of Jarník's algorithm for minimum spanning trees

In computer science and combinatorial optimization, Jarník is known for an algorithm for constructing minimum spanning trees that he published in 1930, in response to the publication of Borůvka's algorithm by another Czech mathematician, Otakar Borůvka.[14] Jarník's algorithm builds a tree from a single starting vertex of a given weighted graph by repeatedly adding the cheapest connection to any other vertex, until all vertices have been connected. The same algorithm was later rediscovered in the late 1950s by Robert C. Prim and Edsger W. Dijkstra. It is also known as Prim's algorithm or the Prim–Dijkstra algorithm.[15]

He also published a second, related, paper with Miloš Kössler (1934) on the Euclidean Steiner tree problem. In this problem, one must again form a tree connecting a given set of points, with edge costs given by the Euclidean distance. However, additional points that are not part of the input may be added to make the overall tree shorter. This paper is the first serious treatment of the general Steiner tree problem (although it appears earlier in a letter by Gauss), and it already contains "virtually all general properties of Steiner trees" later attributed to other researchers.[7]

Recognition and legacy

Jarník was a member of the Czech Academy of Sciences and Arts, from 1934 as an extraordinary member and from 1946 as a regular member.[1] In 1952 he became one of the founding members of Czechoslovak Academy of Sciences.[1][4] He was also awarded the Czechoslovak State Prize in 1952.[1]

Jarníkova Street, the Jarníkova bus stop, and a commemorative sign honoring Jarník

The Vojtěch Jarník International Mathematical Competition, held each year since 1991 in Ostrava, is named in his honor,[16] as is Jarníkova Street in the Chodov district of Prague. A series of postage stamps published by Czechoslovakia in 1987 to honor the 125th anniversary of the Union of Czechoslovak mathematicians and physicists included one stamp featuring Jarník together with Joseph Petzval and Vincenc Strouhal.[17]

A conference was held in Prague, in March 1998, to honor the centennial of his birth.[1]

Selected publications

Jarník published 90 papers in mathematics,[18] including:

  • Jarník, Vojtěch (1923), "O číslech derivovaných funkcí jedné reálné proměnné" [On derivative numbers of functions of a real variable], Časopis Pro Pěstování Matematiky a Fysiky (in Czech), 53: 98–101, JFM 50.0189.02. A function with unbounded variation in all intervals has a dense set of points where a Dini derivative is infinite.[13]
  • Jarník, Vojtěch (1926), "Über die Gitterpunkte auf konvexen Kurven" [On the grid points on convex curves], Mathematische Zeitschrift (in German), 24 (1): 500–518, doi:10.1007/BF01216795, MR 1544776. Tight bounds on the number of integer points on a convex curve, as a function of its length.
  • Jarník, Vojtĕch (1928–1929), "Zur metrischen Theorie der diophantischen Approximationen" [On the metric theory of Diophantine approximations], Prace Matematyczno-Fizyczne (in German), Warszawa, 36: 91–106, JFM 55.0718.01. The badly-approximable numbers have Hausdorff dimension one.[11]
  • Jarník, Vojtĕch (1929), "Diophantische Approximationen und Hausdorffsches Maß" [Diophantine approximation and the Hausdorff measure], Matematicheskii Sbornik (in German), 36: 371–382, JFM 55.0719.01. The well-approximable numbers have Hausdorff dimension less than one.[11]
  • Jarník, Vojtěch (1930), "O jistém problému minimálním. (Z dopisu panu O. Borůvkovi)" [About a certain minimal problem (from a letter to O. Borůvka)], Práce Moravské Přírodovědecké Společnosti (in Czech), 6: 57–63. The original reference for Jarnik's algorithm for minimum spanning trees.[7]
  • Jarník, Vojtěch (1933), "Über die Differenzierbarkeit stetiger Funktionen" [On the differentiability of continuous functions], Fundamenta Mathematicae (in German), 21: 48–58, Zbl 0007.40102. Generic functions have infinite Dini derivatives at almost all points.[13]
  • Jarník, Vojtěch; Kössler, Miloš (1934), "O minimálních grafech, obsahujících n daných bodů" [On minimal graphs containing n given points], Časopis pro Pěstování Matematiky a Fysiky (in Czech), 63: 223–235, Zbl 0009.13106. The first serious treatment of the Steiner tree problem.[7]

He was also the author of ten textbooks in Czech, on integral calculus, differential equations, and mathematical analysis.[18] These books "became classics for several generations of students".[19]

References
  1. Netuka, Ivan (1998), "In memoriam Prof. Vojtěch Jarník (22. 12. 1897 – 22. 9. 1970)" (PDF), News and Notes, Mathematica Bohemica, 123 (2): 219–221.
  2. Durnová (2004), p. 168.
  3. Veselý, Jiří (1999), "Pedagogical activities of Vojtěch Jarník", in Novák, Břetislav (ed.), Life and work of Vojtěch Jarník, Prague: Union of Czech mathematicians and physicists, pp. 83–94, ISBN 80-7196-156-6.
  4. O'Connor, John J.; Robertson, Edmund F., "Vojtěch Jarník", MacTutor History of Mathematics archive, University of St Andrews.
  5. Netuka (1998) and Veselý (1999); however, O'Connor and Robertson give his return dates as 1924 and 1928.
  6. Vojtěch Jarník at the Mathematics Genealogy Project,
  7. Korte, Bernhard; Nešetřil, Jaroslav (2001), "Vojtěch Jarník's work in combinatorial optimization", Discrete Mathematics, 235 (1–3): 1–17, doi:10.1016/S0012-365X(00)00256-9, hdl:10338.dmlcz/500662, MR 1829832.
  8. Bordellès, Olivier (2012), "5.4.7 Counting integer points on smooth curves", Arithmetic Tales, Springer, p. 290, ISBN 9781447140962.
  9. Huxley, M. N. (1996), "2.2 Jarník's polygon", Area, Lattice Points, and Exponential Sums, London Mathematical Society Monographs, 13, Clarendon Press, pp. 31–33, ISBN 9780191590320.
  10. Redmond, Don (1996), Number Theory: An Introduction to Pure and Applied Mathematics, CRC Press, p. 561, ISBN 9780824796969.
  11. Dodson, M. M. (1999), "Some recent extensions of Jarník's work in Diophantine approximation", in Novák, Břetislav (ed.), Life and work of Vojtěch Jarník, Prague: Union of Czech mathematicians and physicists, pp. 23–36, ISBN 80-7196-156-6.
  12. Beresnevich, Victor; Ramírez, Felipe; Velani, Sanju (2016), "Metric Diophantine approximation: Aspects of recent work", in Badziahin, Dzmitry; Gorodnik, Alexander; Peyerimhoff, Norbert (eds.), Dynamics and Analytic Number Theory: Proceedings of the Durham Easter School 2014, London Mathematical Society Lecture Note Series, 437, Cambridge University Press, pp. 1–95, arXiv:1601.01948, doi:10.1017/9781316402696.002. See Theorem 1.33 (the Jarník–Besicovitch theorem), p. 23, and the discussion following the theorem.
  13. Preiss, David (1999), "The work of Professor Jarník in real analysis", in Novák, Břetislav (ed.), Life and work of Vojtěch Jarník, Prague: Union of Czech mathematicians and physicists, pp. 55–66, ISBN 80-7196-156-6.
  14. Durnová, Helena (2004), "A history of discrete optimization", in Fuchs, Eduard (ed.), Mathematics Throughout the Ages, Vol. II, Prague: Výzkumné centrum pro dějiny vědy, pp. 51–184, ISBN 9788072850464. See in particular page 127: "Soon after Borůvka's published his solution, another Czech mathematician, Vojtěch Jarník, reacted by publishing his own solution," and page 133: "Jarník’s article on this topic is an extract from a letter to O. Borůvka".
  15. Sedgewick, Robert; Wayne, Kevin (2011), Algorithms (4th ed.), Addison-Wesley Professional, p. 628, ISBN 9780132762564.
  16. Vojtěch Jarník International Mathematical Competition, retrieved February 16, 2017
  17. Miller, Jeff, Images of Mathematicians on Postage Stamps, retrieved 2017-02-17.
  18. Novák, Břetislav, ed. (1999), "Bibliography of scientific works of V. Jarník", Life and work of Vojtěch Jarník, Prague: Union of Czech mathematicians and physicists, pp. 133–142, ISBN 80-7196-156-6.
  19. Vojtěch Jarník, Czech Digital Mathematics Library, 2010, retrieved 2017-02-17.

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.