Vector fields in cylindrical and spherical coordinates

Note: This page uses common physics notation for spherical coordinates, in which ${\displaystyle \theta }$ is the angle between the z axis and the radius vector connecting the origin to the point in question, while ${\displaystyle \phi }$ is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.[1]

Spherical coordinates (r, θ, φ) as commonly used in physics: radial distance r, polar angle θ (theta), and azimuthal angle φ (phi). The symbol ρ (rho) is often used instead of r.

Cylindrical coordinate system

Vector fields

Vectors are defined in cylindrical coordinates by (ρ, φ, z), where

• ρ is the length of the vector projected onto the xy-plane,
• φ is the angle between the projection of the vector onto the xy-plane (i.e. ρ) and the positive x-axis (0 ≤ φ < 2π),
• z is the regular z-coordinate.

(ρ, φ, z) is given in cartesian coordinates by:

${\displaystyle {\begin{bmatrix}\rho \\\phi \\z\end{bmatrix}}={\begin{bmatrix}{\sqrt {x^{2}+y^{2}}}\\\operatorname {arctan} (y/x)\\z\end{bmatrix}},\ \ \ 0\leq \phi <2\pi ,}$

or inversely by:

${\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}\rho \cos \phi \\\rho \sin \phi \\z\end{bmatrix}}.}$

Any vector field can be written in terms of the unit vectors as:

${\displaystyle \mathbf {A} =A_{x}\mathbf {\hat {x}} +A_{y}\mathbf {\hat {y}} +A_{z}\mathbf {\hat {z}} =A_{\rho }\mathbf {\hat {\rho }} +A_{\phi }{\boldsymbol {\hat {\phi }}}+A_{z}\mathbf {\hat {z}} }$

The cylindrical unit vectors are related to the cartesian unit vectors by:

${\displaystyle {\begin{bmatrix}\mathbf {\hat {\rho }} \\{\boldsymbol {\hat {\phi }}}\\\mathbf {\hat {z}} \end{bmatrix}}={\begin{bmatrix}\cos \phi &\sin \phi &0\\-\sin \phi &\cos \phi &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}}$

Note: the matrix is an orthogonal matrix, that is, its inverse is simply its transpose.

Time derivative of a vector field

To find out how the vector field A changes in time we calculate the time derivatives. For this purpose we use Newton's notation for the time derivative (${\displaystyle {\dot {\mathbf {A} }}}$). In cartesian coordinates this is simply:

${\displaystyle {\dot {\mathbf {A} }}={\dot {A}}_{x}{\hat {\mathbf {x} }}+{\dot {A}}_{y}{\hat {\mathbf {y} }}+{\dot {A}}_{z}{\hat {\mathbf {z} }}}$

However, in cylindrical coordinates this becomes:

${\displaystyle {\dot {\mathbf {A} }}={\dot {A}}_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\rho }{\dot {\hat {\boldsymbol {\rho }}}}+{\dot {A}}_{\phi }{\hat {\boldsymbol {\phi }}}+A_{\phi }{\dot {\hat {\boldsymbol {\phi }}}}+{\dot {A}}_{z}{\hat {\boldsymbol {z}}}+A_{z}{\dot {\hat {\boldsymbol {z}}}}}$

We need the time derivatives of the unit vectors. They are given by:

${\displaystyle {\begin{aligned}{\dot {\hat {\mathbf {\rho } }}}&={\dot {\phi }}{\hat {\boldsymbol {\phi }}}\\{\dot {\hat {\boldsymbol {\phi }}}}&=-{\dot {\phi }}{\hat {\mathbf {\rho } }}\\{\dot {\hat {\mathbf {z} }}}&=0\end{aligned}}}$

So the time derivative simplifies to:

${\displaystyle {\dot {\mathbf {A} }}={\hat {\boldsymbol {\rho }}}({\dot {A}}_{\rho }-A_{\phi }{\dot {\phi }})+{\hat {\boldsymbol {\phi }}}({\dot {A}}_{\phi }+A_{\rho }{\dot {\phi }})+{\hat {\mathbf {z} }}{\dot {A}}_{z}}$

Second time derivative of a vector field

The second time derivative is of interest in physics, as it is found in equations of motion for classical mechanical systems. The second time derivative of a vector field in cylindrical coordinates is given by:

${\displaystyle \mathbf {\ddot {A}} =\mathbf {\hat {\rho }} ({\ddot {A}}_{\rho }-A_{\phi }{\ddot {\phi }}-2{\dot {A}}_{\phi }{\dot {\phi }}-A_{\rho }{\dot {\phi }}^{2})+{\boldsymbol {\hat {\phi }}}({\ddot {A}}_{\phi }+A_{\rho }{\ddot {\phi }}+2{\dot {A}}_{\rho }{\dot {\phi }}-A_{\phi }{\dot {\phi }}^{2})+\mathbf {\hat {z}} {\ddot {A}}_{z}}$

To understand this expression, we substitute A = P, where p is the vector (\rho, θ, z).

This means that ${\displaystyle \mathbf {A} =\mathbf {P} =\rho \mathbf {\hat {\rho }} +z\mathbf {\hat {z}} }$.

After substituting we get:

${\displaystyle {\ddot {\mathbf {P} }}=\mathbf {\hat {\rho }} ({\ddot {\rho }}-\rho {\dot {\phi }}^{2})+{\boldsymbol {\hat {\phi }}}(\rho {\ddot {\phi }}+2{\dot {\rho }}{\dot {\phi }})+\mathbf {\hat {z}} {\ddot {z}}}$

In mechanics, the terms of this expression are called:

${\displaystyle {\begin{aligned}{\ddot {\rho }}\mathbf {\hat {\rho }} &={\mbox{central outward acceleration}}\\-\rho {\dot {\phi }}^{2}\mathbf {\hat {\rho }} &={\mbox{centripetal acceleration}}\\\rho {\ddot {\phi }}{\boldsymbol {\hat {\phi }}}&={\mbox{angular acceleration}}\\2{\dot {\rho }}{\dot {\phi }}{\boldsymbol {\hat {\phi }}}&={\mbox{Coriolis effect}}\\{\ddot {z}}\mathbf {\hat {z}} &={\mbox{z-acceleration}}\end{aligned}}}$

Spherical coordinate system

Vector fields

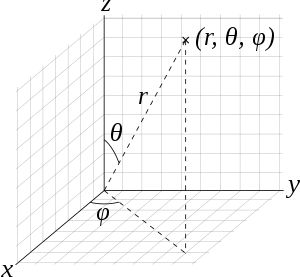
Vectors are defined in spherical coordinates by (r, θ, φ), where

• r is the length of the vector,
• θ is the angle between the positive Z-axis and the vector in question (0 ≤ θ ≤ π), and
• φ is the angle between the projection of the vector onto the X-Y-plane and the positive X-axis (0 ≤ φ < 2π).

(r, θ, φ) is given in Cartesian coordinates by:

${\displaystyle {\begin{bmatrix}r\\\theta \\\phi \end{bmatrix}}={\begin{bmatrix}{\sqrt {x^{2}+y^{2}+z^{2}}}\\\arccos(z/r)\\\arctan(y/x)\end{bmatrix}},\ \ \ 0\leq \theta \leq \pi ,\ \ \ 0\leq \phi <2\pi ,}$

or inversely by:

${\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}r\sin \theta \cos \phi \\r\sin \theta \sin \phi \\r\cos \theta \end{bmatrix}}.}$

Any vector field can be written in terms of the unit vectors as:

${\displaystyle \mathbf {A} =A_{x}\mathbf {\hat {x}} +A_{y}\mathbf {\hat {y}} +A_{z}\mathbf {\hat {z}} =A_{r}{\boldsymbol {\hat {r}}}+A_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\phi }{\boldsymbol {\hat {\phi }}}}$

The spherical unit vectors are related to the cartesian unit vectors by:

${\displaystyle {\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}}\\{\boldsymbol {\hat {\phi }}}\end{bmatrix}}={\begin{bmatrix}\sin \theta \cos \phi &\sin \theta \sin \phi &\cos \theta \\\cos \theta \cos \phi &\cos \theta \sin \phi &-\sin \theta \\-\sin \phi &\cos \phi &0\end{bmatrix}}{\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}}$

Note: the matrix is an orthogonal matrix, that is, its inverse is simply its transpose.

So the cartesian unit vectors are related to the spherical unit vectors by:

${\displaystyle {\begin{bmatrix}\mathbf {\hat {x}} \\\mathbf {\hat {y}} \\\mathbf {\hat {z}} \end{bmatrix}}={\begin{bmatrix}\sin \theta \cos \phi &\cos \theta \cos \phi &-\sin \phi \\\sin \theta \sin \phi &\cos \theta \sin \phi &\cos \phi \\\cos \theta &-\sin \theta &0\end{bmatrix}}{\begin{bmatrix}{\boldsymbol {\hat {r}}}\\{\boldsymbol {\hat {\theta }}}\\{\boldsymbol {\hat {\phi }}}\end{bmatrix}}}$

Time derivative of a vector field

To find out how the vector field A changes in time we calculate the time derivatives. In cartesian coordinates this is simply:

${\displaystyle \mathbf {\dot {A}} ={\dot {A}}_{x}\mathbf {\hat {x}} +{\dot {A}}_{y}\mathbf {\hat {y}} +{\dot {A}}_{z}\mathbf {\hat {z}} }$

However, in spherical coordinates this becomes:

${\displaystyle \mathbf {\dot {A}} ={\dot {A}}_{r}{\boldsymbol {\hat {r}}}+A_{r}{\boldsymbol {\dot {\hat {r}}}}+{\dot {A}}_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\theta }{\boldsymbol {\dot {\hat {\theta }}}}+{\dot {A}}_{\phi }{\boldsymbol {\hat {\phi }}}+A_{\phi }{\boldsymbol {\dot {\hat {\phi }}}}}$

We need the time derivatives of the unit vectors. They are given by:

${\displaystyle {\begin{aligned}{\boldsymbol {\dot {\hat {r}}}}&={\dot {\theta }}{\boldsymbol {\hat {\theta }}}+{\dot {\phi }}\sin \theta {\boldsymbol {\hat {\phi }}}\\{\boldsymbol {\dot {\hat {\theta }}}}&=-{\dot {\theta }}{\boldsymbol {\hat {r}}}+{\dot {\phi }}\cos \theta {\boldsymbol {\hat {\phi }}}\\{\boldsymbol {\dot {\hat {\phi }}}}&=-{\dot {\phi }}\sin \theta {\boldsymbol {\hat {r}}}-{\dot {\phi }}\cos \theta {\boldsymbol {\hat {\theta }}}\end{aligned}}}$

So the time derivative becomes:

${\displaystyle \mathbf {\dot {A}} ={\boldsymbol {\hat {r}}}({\dot {A}}_{r}-A_{\theta }{\dot {\theta }}-A_{\phi }{\dot {\phi }}\sin \theta )+{\boldsymbol {\hat {\theta }}}({\dot {A}}_{\theta }+A_{r}{\dot {\theta }}-A_{\phi }{\dot {\phi }}\cos \theta )+{\boldsymbol {\hat {\phi }}}({\dot {A}}_{\phi }+A_{r}{\dot {\phi }}\sin \theta +A_{\theta }{\dot {\phi }}\cos \theta )}$

See also

• Del in cylindrical and spherical coordinates for the specification of gradient, divergence, curl, and laplacian in various coordinate systems.

References

1. Wolfram Mathworld, spherical coordinates