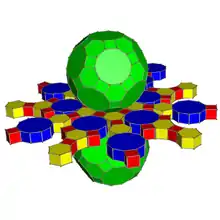
Truncated icosidodecahedral prism
In geometry, a truncated icosidodecahedral prism or great rhombicosidodecahedral prism is a convex uniform 4-polytope (four-dimensional polytope).
| Truncated icosidodecahedral prism | |
|---|---|
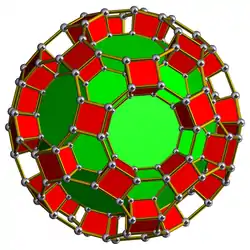 Schlegel diagram | |
| Type | Prismatic uniform 4-polytope |
| Uniform index | 63 |
| Schläfli symbol | t0,1,2,3{3,5,2} or tr{3,5}×{} |
| Coxeter-Dynkin |     |
| Cells | 64 total: |
| Faces | 304 total: 240 {4} 40 {6} 24 {5} |
| Edges | 480 |
| Vertices | 240 |
| Vertex figure | 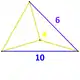 Irregular tetrahedron |
| Symmetry group | [5,3,2], order 240 |
| Properties | convex |
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.
Alternative names
- Truncated icosidodecahedral dyadic prism (Norman W. Johnson)
- Griddip (Jonathan Bowers: for great rhombicosidodecahedral prism/hyperprism)
- Great rhombicosidodecahedral prism/hyperprism
Related polytopes
A full snub dodecahedral antiprism or omnisnub dodecahedral antiprism can be defined as an alternation of an truncated icosidodecahedral prism, represented by ht0,1,2,3{5,3,2}, or 
, although it cannot be constructed as a uniform 4-polytope. It has 184 cells: 2 snub dodecahedrons connected by 30 tetrahedrons, 12 pentagonal antiprisms, and 20 octahedrons, with 120 tetrahedrons in the alternated gaps. It has 120 vertices, 480 edges, and 544 faces (24 pentagons and 40+480 triangles). It has [5,3,2]+ symmetry, order 120.
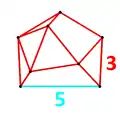
Vertex figure for the omnisnub dodecahedral antiprism
External links
- 6. Convex uniform prismatic polychora - Model 63, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x x3o5x - griddip".