Toffoli gate

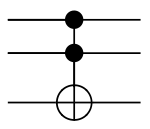
In logic circuits, the Toffoli gate (also CCNOT gate), invented by Tommaso Toffoli, is a universal reversible logic gate, which means that any reversible circuit can be constructed from Toffoli gates. It is also known as the "controlled-controlled-not" gate, which describes its action. It has 3-bit inputs and outputs; if the first two bits are both set to 1, it inverts the third bit, otherwise all bits stay the same.

Circuit representation of Toffoli gate

Background

An input-consuming logic gate L is reversible if, for any output y, there is a unique input x such that applying L(x) = y. If a gate L is reversible, there is an inverse gate L′, which maps y to x for which L′(y) = x. From common logic gates, NOT is reversible, as can be seen from its truth table below.

INPUTOUTPUT
01
10

The common AND gate is not reversible, however. The inputs 00, 01 and 10 are all mapped to the output 0.

Reversible gates have been studied since the 1960s. The original motivation was that reversible gates dissipate less heat (or, in principle, no heat).[1] If we think of a logic gate as consuming its input, information is lost since less information is present in the output than was present at the input. This loss of information loses energy to the surrounding area as heat, because of thermodynamic entropy. Another way to understand this is that charges on a circuit are grounded and thus flow away, taking a small quantity of energy with them when they change state. A reversible gate only moves the states around, and since no information is lost, energy is conserved.

More recent motivation comes from quantum computing. Quantum mechanics requires the transformations to be reversible and allows more general states of the computation than classical computers (superpositions).

Universality and Toffoli gate

Any reversible gate that consumes its inputs and allows all input computations must have no more input bits than output bits, by the pigeonhole principle. For one input bit, there are two possible reversible gates. One of them is NOT. The other is the identity gate, which maps its input to the output unchanged. For two input bits, the only non-trivial gate is the controlled NOT gate, which XORs the first bit to the second bit and leaves the first bit unchanged.

Truth tablePermutation matrix form
INPUT OUTPUT
 0  0  0  0 
0101
1011
1110

Unfortunately, there are reversible functions that cannot be computed using just those gates. In other words, the set consisting of NOT and XOR gates is not universal. If we want to compute an arbitrary function using reversible gates, we need another gate. One possibility is the Toffoli gate, proposed in 1980 by Toffoli.[2]

This gate has 3-bit inputs and outputs. If the first two bits are set, it flips the third bit. The following is a table of the input and output bits:

Truth tablePermutation matrix form
INPUT OUTPUT
 0  0  0  0  0  0 
001001
010010
011011
100100
101101
110111
111110

It can be also described as mapping bits {a, b, c} to {a, b, c XOR (a AND b)}.

The Toffoli gate is universal; this means that for any Boolean function f(x1, x2, ..., xm), there is a circuit consisting of Toffoli gates that takes x1, x2, ..., xm and some extra bits set to 0 or 1 to outputs x1, x2, ..., xm, f(x1, x2, ..., xm), and some extra bits (called garbage). Essentially, this means that one can use Toffoli gates to build systems that will perform any desired Boolean function computation in a reversible manner.

The Toffoli gate can be constructed from single qubit gates and a minimum of six CNOTs.
  • The Fredkin gate is a universal reversible 3-bit gate that swaps the last two bits if the first bit is 1; a controlled-swap operation.
  • The n-bit Toffoli gate is a generalization of Toffoli gate. It takes n bits x1, x2, ..., xn as inputs and outputs n bits. The first n−1 output bits are just x1, ..., xn−1. The last output bit is (x1 AND ... AND xn−1) XOR xn.
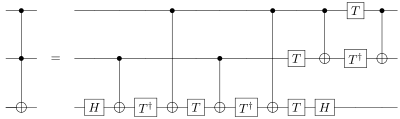
  • The Toffoli gate can be realized by five two-qubit quantum gates.[3]

(It can be shown that this is the optimum, that is, it cannot be realized using less than five.[4])

  • A related quantum gate, the Deutsch gate, can be realized by five optical pulses with neutral atoms.[5] The Deutsch gate is a universal gate for quantum computing.[6]

Relation to quantum computing

Any reversible gate can be implemented on a quantum computer, and hence the Toffoli gate is also a quantum operator. However, the Toffoli gate can not be used for universal quantum computation, though it does mean that a quantum computer can implement all possible classical computations. The Toffoli gate has to be implemented along with some inherently quantum gate(s) in order to be universal for quantum computation. In fact, any single-qubit gate with real coefficients that can create a nontrivial quantum state suffices.[7] A Toffoli gate based on quantum mechanics was successfully realized in January 2009 at the University of Innsbruck, Austria.[8] While the Implementation of n-qubit Toffoli with circuit model requires 2n C-NOT gates,[9] application of many-body interaction could be used for direct operation of the gate in Rydberg atoms and superconducting circuit implementations.[10][11][12]

See also

References
  1. Landauer, R. (July 1961). "Irreversibility and Heat Generation in the Computing Process". IBM Journal of Research and Development. 5 (3): 183–191. doi:10.1147/rd.53.0183. ISSN 0018-8646.
  2. Technical Report MIT/LCS/TM-151 (1980) and an adapted and condensed version: Toffoli, Tommaso (1980). J. W. de Bakker and J. van Leeuwen (ed.). Reversible computing (PDF). Automata, Languages and Programming, Seventh Colloquium. Noordwijkerhout, Netherlands: Springer Verlag. pp. 632–644. doi:10.1007/3-540-10003-2_104. ISBN 3-540-10003-2. Archived from the original (PDF) on 2010-04-15.
  3. Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A.; Weinfurter, Harald (Nov 1995). "Elementary gates for quantum computation". Physical Review A. American Physical Society. 52 (5): 3457–3467. arXiv:quant-ph/9503016. Bibcode:1995PhRvA..52.3457B. doi:10.1103/PhysRevA.52.3457. PMID 9912645. S2CID 8764584.
  4. Yu, Nengkun; Duan, Runyao; Ying, Mingsheng (2013-07-30). "Five two-qubit gates are necessary for implementing the Toffoli gate". Physical Review A. 88 (1): 010304. arXiv:1301.3372. Bibcode:2013PhRvA..88a0304Y. doi:10.1103/physreva.88.010304. ISSN 1050-2947. S2CID 55486826.
  5. Shi, Xiao-Feng (May 2018). "Deutsch, Toffoli, and CNOT Gates via Rydberg Blockade of Neutral Atoms". Physical Review Applied. 9 (5): 051001. arXiv:1710.01859. Bibcode:2018PhRvP...9e1001S. doi:10.1103/PhysRevApplied.9.051001. S2CID 118909059.
  6. Deutsch, D. (1989). "Quantum Computational Networks". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 425 (1868): 73–90. Bibcode:1989RSPSA.425...73D. doi:10.1098/rspa.1989.0099. ISSN 0080-4630. JSTOR 2398494. S2CID 123073680.
  7. Shi, Yaoyun (Jan 2003). "Both Toffoli and Controlled-NOT need little help to do universal quantum computation". Quantum Information & Computation. 3 (1): 84–92. arXiv:quant-ph/0205115. Bibcode:2002quant.ph..5115S.
  8. Monz, T.; Kim, K.; Hänsel, W.; Riebe, M.; Villar, A. S.; Schindler, P.; Chwalla, M.; Hennrich, M.; Blatt, R. (Jan 2009). "Realization of the Quantum Toffoli Gate with Trapped Ions". Physical Review Letters. American Physical Society. 102 (4): 040501. arXiv:0804.0082. Bibcode:2009PhRvL.102d0501M. doi:10.1103/PhysRevLett.102.040501. PMID 19257408. S2CID 2051775.
  9. Shende, Vivek V.; Markov, Igor L. (2008-03-15). "On the CNOT-cost of TOFFOLI gates". arXiv:0803.2316 [quant-ph].
  10. Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. Bibcode:2020PhRvX..10b1054K. doi:10.1103/PhysRevX.10.021054. ISSN 2160-3308.
  11. Isenhower, L.; Saffman, M.; Mølmer, K. (2011-09-04). "Multibit CkNOT quantum gates via Rydberg blockade". Quantum Information Processing. 10 (6): 755. arXiv:1104.3916. doi:10.1007/s11128-011-0292-4. ISSN 1573-1332. S2CID 28732092.
  12. Rasmussen, S. E.; Groenland, K.; Gerritsma, R.; Schoutens, K.; Zinner, N. T. (2020-02-07). "Single-step implementation of high-fidelity n -bit Toffoli gates". Physical Review A. 101 (2): 022308. arXiv:1910.07548. Bibcode:2020PhRvA.101b2308R. doi:10.1103/physreva.101.022308. ISSN 2469-9926. S2CID 204744044.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.