Statistical interference

When two probability distributions overlap, statistical interference exists. Knowledge of the distributions can be used to determine the likelihood that one parameter exceeds another, and by how much.

Not to be confused with Statistical inference.

This technique can be used for dimensioning of mechanical parts, determining when an applied load exceeds the strength of a structure, and in many other situations. This type of analysis can also be used to estimate the probability of failure or the frequency of failure.

Dimensional interference
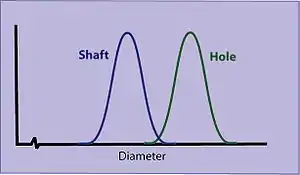
Interference of measurement distributions to determine fit of parts

Mechanical parts are usually designed to fit precisely together. For example, if a shaft is designed to have a "sliding fit" in a hole, the shaft must be a little smaller than the hole. (Traditional tolerances may suggest that all dimensions fall within those intended tolerances. A process capability study of actual production, however, may reveal normal distributions with long tails.) Both the shaft and hole sizes will usually form normal distributions with some average (arithmetic mean) and standard deviation.

With two such normal distributions, a distribution of interference can be calculated. The derived distribution will also be normal, and its average will be equal to the difference between the means of the two base distributions. The variance of the derived distribution will be the sum of the variances of the two base distributions.

This derived distribution can be used to determine how often the difference in dimensions will be less than zero (i.e., the shaft cannot fit in the hole), how often the difference will be less than the required sliding gap (the shaft fits, but too tightly), and how often the difference will be greater than the maximum acceptable gap (the shaft fits, but not tightly enough).

Physical property interference
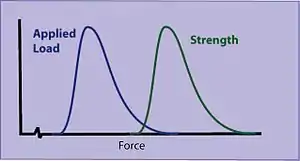
Interference of distributions of applied load and strength

Physical properties and the conditions of use are also inherently variable. For example, the applied load (stress) on a mechanical part may vary. The measured strength of that part (tensile strength, etc.) may also be variable. The part will break when the stress exceeds the strength.[1] [2]

With two normal distributions, the statistical interference may be calculated as above. (This problem is also workable for transformed units such as the log-normal distribution). With other distributions, or combinations of different distributions, a Monte Carlo method or simulation is often the most practical way to quantify the effects of statistical interference.

See also

References
  1. Sundarth, S; Woeste, Frank E.; Galligan, William (1978), Differential reliability : probabilistic engineering applied to wood members in bending-tension (PDF), Res. Pap. FPL-RP-302., US Forest Products Laboratory, retrieved 21 January 2015CS1 maint: multiple names: authors list (link)
  2. Long, M W; Narcico, J D (June 1999), Probabilistic Design Methodology for Composite Aircraft Structures, DOT/FAA/AR-99/2, FAA, retrieved 24 January 2015
  • Paul H. Garthwaite, Byron Jones, Ian T. Jolliffe (2002) Statistical Inference. ISBN 0-19-857226-3
  • Haugen, (1980) Probabilistic mechanical design, Wiley. ISBN 0-471-05847-5
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.