Sousselier graph

The Sousselier graph is, in graph theory, a hypohamiltonian graph with 16 vertices and 27 edges. It has book thickness 3 and queue number 2.[1]

Sousselier graph
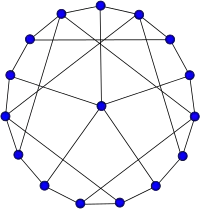Vertices16
Edges27
Radius2
Diameter3
Girth5
Automorphisms2
Chromatic number3
Chromatic index5
Book thickness3
Queue number2
Table of graphs and parameters

History

Hypohamiltonian graphs were first studied by Sousselier in Problèmes plaisants et délectables (1963) .[2]

In 1967, Lindgren builds an infinite sequence of hypohamiltonian graphs. The graphs of this sequence all have 6k+10 vertices, for every integer k.[3] The same sequence of hypohamiltonian graphs is independently built by Sousselier.[4] In 1973 Chvátal explains in a scientific paper how edges can be added to some hypohamiltonian graphs in order to build new ones of the same order, and he names Bondy [5] as the original author of the method. As an illustration, he shows that two edges can be added to the second graph of the Lindgren sequence (which he names Sousselier sequence) in order to build a new hypohamiltonian graph on 16 vertices. This graph is named the Sousselier graph.

References
  1. Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
  2. Sousselier, R. (1963), Problème no. 29: Le cercle des irascibles, 7, Rev. Franç. Rech. Opérationnelle, pp. 405–406
  3. Lindgren, W. F. (1967), "An infinite class of hypohamiltonian graphs", American Mathematical Monthly, 74: 1087–1089, doi:10.2307/2313617, MR0224501
  4. Herz, J. C.; Duby, J. J.; Vigué, F. (1967). "Recherche systématique des graphes hypohamiltoniens". Theory of Graphs. Dunod. pp. 153–159.
  5. V. Chvátal (1973), "Flip-flops in hypo-Hamiltonian graphs", Canadian Mathematical Bulletin, 16: 33–41, doi:10.4153/cmb-1973-008-9
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.