Smoothed octagon

The smoothed octagon is a region in the plane found by Karl Reinhardt in 1934 and conjectured by him to have the lowest maximum packing density of the plane of all centrally symmetric convex shapes.[1] It is constructed by replacing the corners of a regular octagon with a section of a hyperbola that is tangent to the two sides adjacent to the corner and asymptotic to the sides adjacent to these.

A smoothed octagon.

The family of maximally dense packings of the smoothed octagon.

Construction

The corners of the smoothed octagon can be found by rotating three regular octagons whose centres form a triangle with constant area.

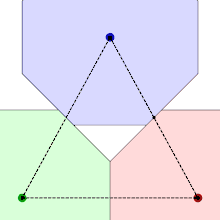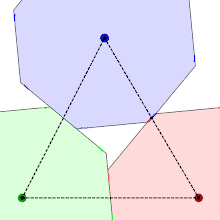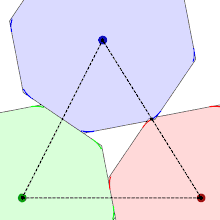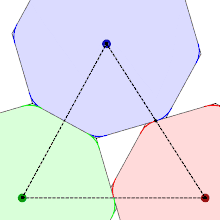
The shape of the smoothed octagon can be derived from its packings, which place octagons at the points of a triangular lattice. The requirement that these packings have the same density no matter how the lattice and smoothed octagon are rotated relative to each other, with shapes that remain in contact with each neighboring shape, can be used to determine the shape of the corners. One of the figures shows three octagons that rotate while the area of the triangle formed by their centres remains constant, keeping them packed together as closely as possible. For regular octagons, the red and blue shapes would overlap, so to enable the rotation to proceed the corners are clipped to a point that lies halfway between their centres, generating the required curve, which turns out to be a hyperbola.

Construction of the smoothed octagon (black), the tangent hyperbola (red) and the asymptotes of this hyperbola (green), and the tangent sides to the hyperbola (blue).

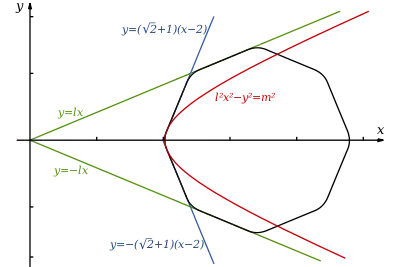
The hyperbola is constructed tangent to two sides of the octagon, and asymptotic to the two adjacent to these. The following details apply to a regular octagon of circumradius ${\displaystyle {\sqrt {2}}}$ with its centre at the point ${\displaystyle (2+{\sqrt {2}},0)}$ and one vertex at the point ${\displaystyle (2,0)}$. We define two constants, ℓ and m:

${\displaystyle \ell ={\sqrt {2}}-1}$

${\displaystyle m={\sqrt[{4}]{\frac {1}{2}}}}$

The hyperbola is then given by the equation

${\displaystyle \ell ^{2}x^{2}-y^{2}=m^{2}}$

or the equivalent parameterization (for the right-hand branch only):

${\displaystyle {\begin{cases}x={\frac {m}{\ell }}\cosh {t}\\y=m\sinh {t}\end{cases}}-\infty <t<\infty }$

The portion of the hyperbola that forms the corner is given by

${\displaystyle -{\frac {\ln {2}}{4}}<t<{\frac {\ln {2}}{4}}}$

The lines of the octagon tangent to the hyperbola are

${\displaystyle y=\pm \left({\sqrt {2}}+1\right)\left(x-2\right)}$

The lines asymptotic to the hyperbola are simply

${\displaystyle y=\pm \ell x.}$

Packing

The smoothed octagon has a maximum packing density given by

${\displaystyle {\frac {8-4{\sqrt {2}}-\ln {2}}{2{\sqrt {2}}-1}}\approx 0.902414\,.}$[2]

This is lower than the maximum packing density of circles, which is

${\displaystyle {\frac {\pi }{\sqrt {12}}}\approx 0.906899.}$

The maximum packing density of the ordinary regular octagon is

${\displaystyle {\frac {4+4{\sqrt {2}}}{5+4{\sqrt {2}}}}\approx 0.906163,}$

also slightly less than the maximum packing density of circles, but higher than that of the smoothed octagon.[3]

Unsolved problem in mathematics: Is the smoothed octagon the centrally symmetric shape with the lowest maximum packing density? (more unsolved problems in mathematics)

The smoothed octagon achieves its maximum packing density, not just for a single packing, but for a 1-parameter family. All of these are lattice packings. Reinhardt's conjecture that the smoothed octagon has the lowest maximum packing density of all centrally symmetric convex shapes in the plane remains unsolved. If central symmetry is not required, the regular heptagon has even lower packing density, but it optimality is also unproven. In three dimensions, Ulam's packing conjecture states that no convex shape has a lower maximum packing density than the ball.[4]

References

1. Reinhardt, K. (1934). "Über die dichteste gitterförmige Lagerung kongruenter Bereiche in der Ebene und eine besondere Art konvexer Kurven". Abh. Math. Sem. Hamburg. 10: 216–230.
2. Weisstein, Eric W. "Smoothed Octagon". MathWorld.
3. Atkinson, Steven; Jiao, Yang; Torquato, Salvatore (2012-09-10). "Maximally dense packings of two-dimensional convex and concave noncircular particles" (PDF). Physical Review E. 86 (3): 031302. arXiv:1405.0245. Bibcode:2012PhRvE..86c1302A. doi:10.1103/physreve.86.031302. PMID 23030907. Archived from the original (PDF) on 2014-08-24.
4. Kallus, Yoav; Kusner, Wöden (2016). "The local optimality of the double lattice packing". Discrete & Computational Geometry. 56 (2): 449–471. arXiv:1509.02241. doi:10.1007/s00454-016-9792-4. MR 3530975.

External links

• The thinnest densest two-dimensional packing?. Peter Scholl, 2001.