Recurrence plot
In descriptive statistics and chaos theory, a recurrence plot (RP) is a plot showing, for each moment i in time, the times at which a phase space trajectory visits roughly the same area in the phase space as at time j. In other words, it is a graph of
showing on a horizontal axis and on a vertical axis, where is a phase space trajectory.
Background
Natural processes can have a distinct recurrent behaviour, e.g. periodicities (as seasonal or Milankovich cycles), but also irregular cyclicities (as El Niño Southern Oscillation). Moreover, the recurrence of states, in the meaning that states are again arbitrarily close after some time of divergence, is a fundamental property of deterministic dynamical systems and is typical for nonlinear or chaotic systems (cf. Poincaré recurrence theorem). The recurrence of states in nature has been known for a long time and has also been discussed in early work (e.g. Henri Poincaré 1890).
Detailed description
Eckmann et al. (1987) introduced recurrence plots, which provide a way to visualize the periodic nature of a trajectory through a phase space. Often, the phase space does not have a low enough dimension (two or three) to be pictured, since higher-dimensional phase spaces can only be visualized by projection into the two or three-dimensional sub-spaces. However, making a recurrence plot enables us to investigate certain aspects of the m-dimensional phase space trajectory through a two-dimensional representation.
A recurrence is a time the trajectory returns to a location it has visited before. The recurrence plot depicts the collection of pairs of times at which the trajectory is at the same place, i.e. the set of with . To make the plot, continuous time and continuous phase space are discretized, taking e.g. as the location of the trajectory at time and counting as a recurrence any time the trajectory gets sufficiently close (say, within ε) to a point it has been previously.
Operationally the plot is drawn as follows:
(a) A certain time window is chosen where any two time steps are separated by the time interval , and where the state of the system is recorded for each time step, thus collecting the trajectory .
(b) A 2D plot is created where the x-axis and y-axis both report , forming a lattice of little squares each with side measuring
(c) The data are used to compute a matrix formed by binary elements recording the recurrence/non-recurrence of values through the binary function:
where .
(d) The recurrence plot then visualises with a black little square of the lattice at coordinates if , and a white little square if .
The visual appearance of a recurrence plot gives hints about the dynamics of the system. Caused by characteristic behaviour of the phase space trajectory, a recurrence plot contains typical small-scale structures, as single dots, diagonal lines and vertical/horizontal lines (or a mixture of the latter, which combines to extended clusters). The large-scale structure, also called texture, can be visually characterised by homogenous, periodic, drift or disrupted. For example, the plot can show if the trajectory is strictly periodic with period , then all such pairs of times will be separated by a multiple of and visible as diagonal lines.
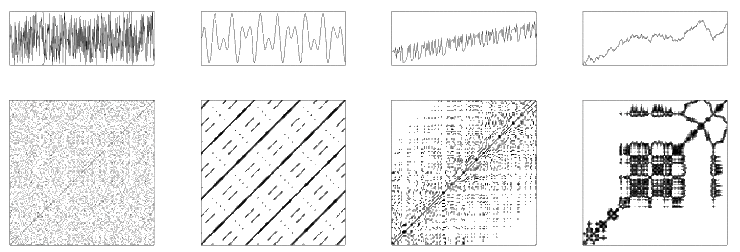
The small-scale structures in RPs are used by the recurrence quantification analysis (Zbilut & Webber 1992; Marwan et al. 2002). This quantification allows us to describe the RPs in a quantitative way and to study transitions or nonlinear parameters of the system. In contrast to the heuristic approach of the recurrence quantification analysis, which depends on the choice of the embedding parameters, some dynamical invariants as correlation dimension, K2 entropy or mutual information, which are independent on the embedding, can also be derived from recurrence plots. The base for these dynamical invariants are the recurrence rate and the distribution of the lengths of the diagonal lines.
Close returns plots are similar to recurrence plots. The difference is that the relative time between recurrences is used for the -axis (instead of absolute time).
The main advantage of recurrence plots is that they provide useful information even for short and non-stationary data, where other methods fail.
Extensions
Multivariate extensions of recurrence plots were developed as cross recurrence plots and joint recurrence plots.
Cross recurrence plots consider the phase space trajectories of two different systems in the same phase space (Marwan & Kurths 2002):
The dimension of both systems must be the same, but the number of considered states (i.e. data length) can be different. Cross recurrence plots compare the occurrences of similar states of two systems. They can be used in order to analyse the similarity of the dynamical evolution between two different systems, to look for similar matching patterns in two systems, or to study the time-relationship of two similar systems, whose time-scale differ (Marwan & Kurths 2005).
Joint recurrence plots are the Hadamard product of the recurrence plots of the considered sub-systems (Romano et al. 2004), e.g. for two systems and the joint recurrence plot is
In contrast to cross recurrence plots, joint recurrence plots compare the simultaneous occurrence of recurrences in two (or more) systems. Moreover, the dimension of the considered phase spaces can be different, but the number of the considered states has to be the same for all the sub-systems. Joint recurrence plots can be used in order to detect phase synchronisation.
Example
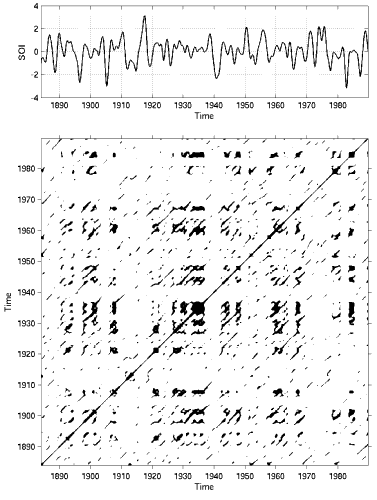
See also
- Poincaré plot
- Recurrence period density entropy, an information-theoretic method for summarising the recurrence properties of both deterministic and stochastic dynamical systems.
- Recurrence quantification analysis, a heuristic approach to quantify recurrence plots.
- Self-similarity matrix
- Dot plot (bioinformatics)
References
- J. P. Eckmann, S. O. Kamphorst, D. Ruelle (1987). "Recurrence Plots of Dynamical Systems". Europhysics Letters. 5 (9): 973–977. Bibcode:1987EL......4..973E. doi:10.1209/0295-5075/4/9/004.CS1 maint: multiple names: authors list (link)
- N. Marwan; M. C. Romano; M. Thiel; J. Kurths (2007). "Recurrence Plots for the Analysis of Complex Systems". Physics Reports. 438 (5–6): 237. Bibcode:2007PhR...438..237M. doi:10.1016/j.physrep.2006.11.001.
- N. Marwan (2008). "A historical review of recurrence plots". European Physical Journal ST. 164 (1): 3–12. arXiv:1709.09971. Bibcode:2008EPJST.164....3M. doi:10.1140/epjst/e2008-00829-1.