Piston motion equations

The motion of a non-offset piston connected to a crank through a connecting rod (as would be found in internal combustion engines), can be expressed through several mathematical equations. This article shows how these motion equations are derived, and shows an example graph.

Crankshaft geometry

Diagram showing geometric layout of piston pin, crank pin and crank center

Definitions

${\displaystyle l}$ rod length (distance between piston pin and crank pin)

${\displaystyle r}$ crank radius (distance between crank pin and crank center, i.e. half stroke)

${\displaystyle A}$ crank angle (from cylinder bore centerline at TDC)

${\displaystyle x}$ piston pin position (upward from crank center along cylinder bore centerline)

${\displaystyle v}$ piston pin velocity (upward from crank center along cylinder bore centerline)

${\displaystyle a}$ piston pin acceleration (upward from crank center along cylinder bore centerline)

${\displaystyle \omega }$ crank angular velocity

Angular velocity

The crankshaft angular velocity is related to the engine revolutions per minute (RPM):

${\displaystyle \omega ={\frac {2\pi \cdot \mathrm {RPM} }{60}}}$

Triangle relation

As shown in the diagram, the crank pin, crank center and piston pin form triangle NOP.
By the cosine law it is seen that:

${\displaystyle l^{2}=r^{2}+x^{2}-2\cdot r\cdot x\cdot \cos A}$

Equations with respect to angular position (Angle Domain)

The equations that follow describe the reciprocating motion of the piston with respect to crank angle. Example graphs of these equations are shown below.

Position

Position with respect to crank angle (from the triangle relation, completing the square, utilizing the Pythagorean identity, and rearranging):

${\displaystyle {\begin{array}{lcl}l^{2}=r^{2}+x^{2}-2\cdot r\cdot x\cdot \cos A\\l^{2}-r^{2}=(x-r\cdot \cos A)^{2}-r^{2}\cdot \cos ^{2}A\\l^{2}-r^{2}+r^{2}\cdot \cos ^{2}A=(x-r\cdot \cos A)^{2}\\l^{2}-r^{2}\cdot (1-\cos ^{2}A)=(x-r\cdot \cos A)^{2}\\l^{2}-r^{2}\cdot \sin ^{2}A=(x-r\cdot \cos A)^{2}\\x=r\cdot \cos A+{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}\\\end{array}}}$

Velocity

Velocity with respect to crank angle (take first derivative, using the chain rule):

${\displaystyle {\begin{array}{lcl}x'&=&{\frac {dx}{dA}}\\&=&-r\cdot \sin A+{\frac {({\frac {1}{2}})\cdot (-2)\cdot r^{2}\cdot \sin A\cdot \cos A}{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}}\\&=&-r\cdot \sin A-{\frac {r^{2}\cdot \sin A\cdot \cos A}{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}}\\\end{array}}}$

( if you desire to manipulate this further, please add a subsection here, including a explanation of intent (e.g. "to isolate sin terms") ).

Acceleration

Acceleration with respect to crank angle (take second derivative, using the chain rule and the quotient rule):

${\displaystyle {\begin{array}{lcl}x''&=&{\frac {d^{2}x}{dA^{2}}}\\&=&-r\cdot \cos A-{\frac {r^{2}\cdot \cos ^{2}A}{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}}-{\frac {-r^{2}\cdot \sin ^{2}A}{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}}-{\frac {r^{2}\cdot \sin A\cdot \cos A\cdot \left(-{\frac {1}{2}}\right)\cdot (-2)\cdot r^{2}\cdot \sin A\cdot \cos A}{\left({\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}\right)^{3}}}\\&=&-r\cdot \cos A-{\frac {r^{2}\cdot \left(\cos ^{2}A-\sin ^{2}A\right)}{\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}}-{\frac {r^{4}\cdot \sin ^{2}A\cdot \cos ^{2}A}{\left({\sqrt {l^{2}-r^{2}\cdot \sin ^{2}A}}\right)^{3}}}\\\end{array}}}$

( if you desire to manipulate this further, please add a subsection here, including a explanation of intent (e.g. "to isolate sin terms") ).

Equations with respect to time (time domain)

Angular velocity derivatives

If angular velocity is constant, then

${\displaystyle A=\omega t\,}$

and the following relations apply:

${\displaystyle {\frac {dA}{dt}}=\omega }$

${\displaystyle {\frac {d^{2}A}{dt^{2}}}=0}$

Converting from angle domain to time domain

The equations that follow describe the reciprocating motion of the piston with respect to time. If time domain is required instead of angle domain, first replace A with ωt in the equations, and then scale for angular velocity as follows:

Position

Position with respect to time is simply:

${\displaystyle x\,}$

Velocity

Velocity with respect to time (using the chain rule):

${\displaystyle {\begin{array}{lcl}v&=&{\frac {dx}{dt}}\\&=&{\frac {dx}{dA}}\cdot {\frac {dA}{dt}}\\&=&{\frac {dx}{dA}}\cdot \ \omega \\&=&x'\cdot \omega \\\end{array}}}$

Acceleration

Acceleration with respect to time (using the chain rule and product rule, and the angular velocity derivatives):

${\displaystyle {\begin{array}{lcl}a&=&{\frac {d^{2}x}{dt^{2}}}\\&=&{\frac {d}{dt}}{\frac {dx}{dt}}\\&=&{\frac {d}{dt}}({\frac {dx}{dA}}\cdot {\frac {dA}{dt}})\\&=&{\frac {d}{dt}}({\frac {dx}{dA}})\cdot {\frac {dA}{dt}}+{\frac {dx}{dA}}\cdot {\frac {d}{dt}}({\frac {dA}{dt}})\\&=&{\frac {d}{dA}}({\frac {dx}{dA}})\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot ({\frac {dA}{dt}})^{2}+{\frac {dx}{dA}}\cdot {\frac {d^{2}A}{dt^{2}}}\\&=&{\frac {d^{2}x}{dA^{2}}}\cdot \omega ^{2}+{\frac {dx}{dA}}\cdot 0\\&=&x''\cdot \omega ^{2}\\\end{array}}}$

Scaling for angular velocity

You can see that x is unscaled, x' is scaled by ω, and x" is scaled by ω². To convert x' from velocity vs angle [inch/rad] to velocity vs time [inch/s] multiply x' by ω [rad/s]. To convert x" from acceleration vs angle [inch/rad²] to acceleration vs time [inch/s²] multiply x" by ω² [rad²/s²]. Note that dimensional analysis shows that the units are consistent.

Velocity maxima/minima

Acceleration zero crossings

The velocity maxima and minima occur at crank angles where the acceleration is zero (crossing the horizontal axis). The velocity maxima and minima depend on rod length (l) and half stroke (r), and do not occur at crank angles (A) of ±90°.

Crank-rod angle not right angled

The velocity maxima and minima do not necessarily occur when the crank makes a right angle with the rod. Counter-examples exist to disprove the idea that velocity maxima and minima only occur when the crank-rod angle is right angled.

Example

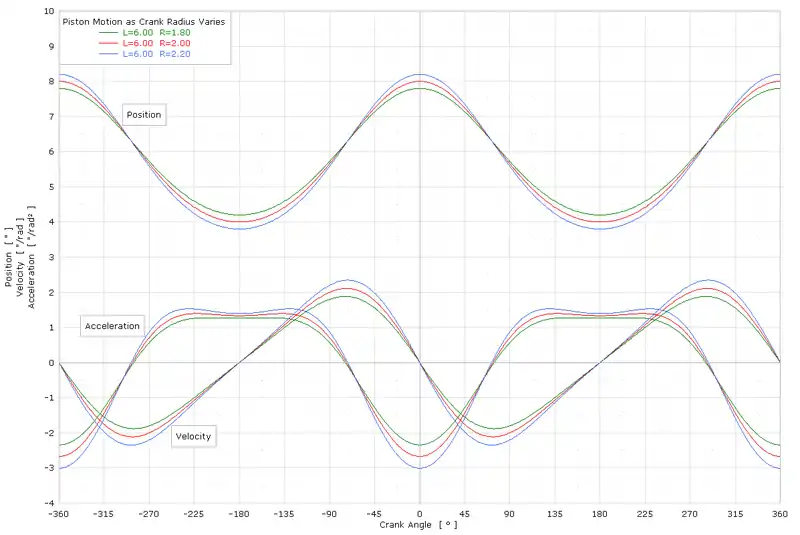
For rod length 6" and crank radius 2" (as shown in the example graph below), numerically solving the acceleration zero-crossings finds the velocity maxima/minima to be at crank angles of ±73.17615°. Then, using the triangle law of sines, it is found that the rod-vertical angle is 18.60647° and the crank-rod angle is 88.21738°. Clearly, in this example, the angle between the crank and the rod is not a right angle. Summing the angles of the triangle 88.21738° + 18.60647° + 73.17615° gives 180.00000°. A single counter-example is sufficient to disprove the statement "velocity maxima/minima occur when crank makes a right angle with rod".

Example graph of piston motion

The graph shows x, x', x" with respect to crank angle for various half strokes, where L = rod length (l) and R = half stroke (r):

The vertical axis units are inches for position, [inches/rad] for velocity, [inches/rad²] for acceleration.
The horizontal axis units are crank angle degrees.

Piston motion animation with same rod length and crank radius values in graph above:

Pistons motion animation with various half strokes

See also

• Internal combustion engine
• Reciprocating engine
• Slider-crank linkage
• Scotch yoke

References

1. http://www.epi-eng.com/piston_engine_technology/piston_motion_basics.htm

Further reading

• John Benjamin Heywood, Internal Combustion Engine Fundamentals, McGraw Hill, 1989.
• Charles Fayette Taylor, The Internal Combustion Engine in Theory and Practice, Vol. 1 & 2, 2nd Edition, MIT Press 1985.

External links

• epi-eng Piston Motion
• codecogs Velocity and Acceleration of a Piston
• animated engines Four Stroke Engine
• desmos interactive crank animation
• networcs D & T Mechanisms - Interactive Tools for Teachers
• mecamedia piston motion animation

• youtube Rotating chevy 350 short block.
• youtube 3D animation of a V8 ENGINE
• youtube Inside a V8 Engine at Idle Speed
• desmos interactive stroke vs rod ratio piston position and derivatives