Neville theta functions

In mathematics, the Neville theta functions, named after Eric Harold Neville,[1] are defined as follows:[2][3] [4]

${\displaystyle \theta _{c}(z,m)={\frac {{\sqrt {2\pi }}\,q(m)^{1/4}}{m^{1/4}{\sqrt {K(m)}}}}\,\,\sum _{k=0}^{\infty }(q(m))^{k(k+1)}\cos \left({\frac {(2k+1)\pi z}{2K(m)}}\right)}$

${\displaystyle \theta _{d}(z,m)={\frac {\sqrt {2\pi }}{2{\sqrt {K(m)}}}}\,\,\left(1+2\,\sum _{k=1}^{\infty }(q(m))^{k^{2}}\cos \left({\frac {\pi zk}{K(m)}}\right)\right)}$

${\displaystyle \theta _{n}(z,m)={\frac {\sqrt {2\pi }}{2(1-m)^{1/4}{\sqrt {K(m)}}}}\,\,\left(1+2\sum _{k=1}^{\infty }(-1)^{k}(q(m))^{k^{2}}\cos \left({\frac {\pi zk}{K(m)}}\right)\right)}$

${\displaystyle \theta _{s}(z,m)={\frac {{\sqrt {2\pi }}\,q(m)^{1/4}}{m^{1/4}(1-m)^{1/4}{\sqrt {K(m)}}}}\,\,\sum _{k=0}^{\infty }(-1)^{k}(q(m))^{k(k+1)}\sin \left({\frac {(2k+1)\pi z}{2K(m)}}\right)}$

where: K(m) is the complete elliptic integral of the first kind, K'(m)=K(1-m), and ${\displaystyle q(m)=e^{-\pi K'(m)/K(m)}}$ is the elliptic nome.

Note that the functions θ_p(z,m) are sometimes defined in terms of the nome q(m) and written θ_p(z,q) (e.g. NIST[5]). The functions may also be written in terms of the τ parameter θ_p(z|τ) where ${\displaystyle q=e^{i\pi \tau }}$.

Relationship to other functions

The Neville theta functions may be expressed in terms of the Jacobi theta functions[5]

${\displaystyle \theta _{s}(z|\tau )=\theta _{23}(0|\tau )\theta _{1}(z'|\tau )/\theta '_{1}(0|\tau )}$

${\displaystyle \theta _{c}(z|\tau )=\theta _{2}(z'|\tau )/\theta _{2}(0|\tau )}$

${\displaystyle \theta _{n}(z|\tau )=\theta _{4}(z'|\tau )/\theta _{4}(0|\tau )}$

${\displaystyle \theta _{d}(z|\tau )=\theta _{3}(z'|\tau )/\theta _{3}(0|\tau )}$

where ${\displaystyle z'=z/\theta _{3}(0|\tau )^{2}}$.

The Neville theta functions are related to the Jacobi elliptic functions. If pq(u,m) is a Jacobi elliptic function (p and q are one of s,c,n,d), then

${\displaystyle \operatorname {pq} (u,m)={\frac {\theta _{p}(u,m)}{\theta _{q}(u,m)}}}$

Examples

Substitute z = 2.5, m = 0.3 into the above definitions of Neville theta functions (using Maple) once obtain the following (consistent with results from wolfram math).

• ${\displaystyle \theta _{c}(2.5,0.3)=-0.65900466676738154967}$[6]
• ${\displaystyle \theta _{d}(2.5,0.3)=0.95182196661267561994}$
• ${\displaystyle \theta _{n}(2.5,0.3)=1.0526693354651613637}$
• ${\displaystyle \theta _{s}(2.5,0.3)=0.82086879524530400536}$

Symmetry

• ${\displaystyle \theta _{c}(z,m)=\theta _{c}(-z,m)}$
• ${\displaystyle \theta _{d}(z,m)=\theta _{d}(-z,m)}$
• ${\displaystyle \theta _{n}(z,m)=\theta _{n}(-z,m)}$
• ${\displaystyle \theta _{s}(z,m)=-\theta _{s}(-z,m)}$

Complex 3D plots

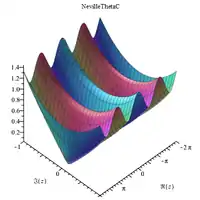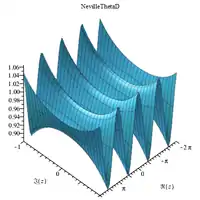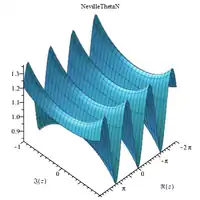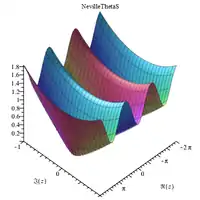Implementation

NetvilleThetaC[z,m], NevilleThetaD[z,m], NevilleThetaN[z,m], and NevilleThetaS[z,m] are built-in functions of Mathematica[7] No such functions in Maple.

Notes

1. Abramowitz and Stegun, pp. 578-579
2. Neville (1944)
3. wolfram Mathematic
4. wolfram math
5. Olver, F. W. J.; et al., eds. (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. Retrieved 2018-02-26.

References

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
• Neville, E. H. (Eric Harold) (1944). Jacobian Elliptic Functions. Oxford Clarendon Press.
• Weisstein, Eric W. "Neville Theta Functions". MathWorld.