Multibody system

Multibody system is the study of the dynamic behavior of interconnected rigid or flexible bodies, each of which may undergo large translational and rotational displacements.

Introduction

The systematic treatment of the dynamic behavior of interconnected bodies has led to a large number of important multibody formalisms in the field of mechanics. The simplest bodies or elements of a multibody system were treated by Newton (free particle) and Euler (rigid body). Euler introduced reaction forces between bodies. Later, a series of formalisms were derived, only to mention Lagrange’s formalisms based on minimal coordinates and a second formulation that introduces constraints.

Basically, the motion of bodies is described by their kinematic behavior. The dynamic behavior results from the equilibrium of applied forces and the rate of change of momentum. Nowadays, the term multibody system is related to a large number of engineering fields of research, especially in robotics and vehicle dynamics. As an important feature, multibody system formalisms usually offer an algorithmic, computer-aided way to model, analyze, simulate and optimize the arbitrary motion of possibly thousands of interconnected bodies.

Applications

While single bodies or parts of a mechanical system are studied in detail with finite element methods, the behavior of the whole multibody system is usually studied with multibody system methods within the following areas:

Aerospace engineering (helicopter, landing gears, behavior of machines under different gravity conditions)
Biomechanics
Combustion engine, gears and transmissions, chain drive, belt drive
Dynamic simulation
Hoist, conveyor, paper mill
Military applications
Particle simulation (granular media, sand, molecules)
Physics engine
Robotics
Vehicle simulation (vehicle dynamics, rapid prototyping of vehicles, improvement of stability, comfort optimization, improvement of efficiency, ...)

Example

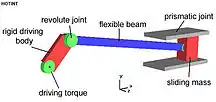
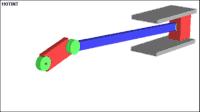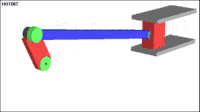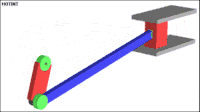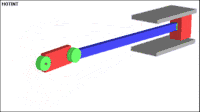
The following example shows a typical multibody system. It is usually denoted as slider-crank mechanism. The mechanism is used to transform rotational motion into translational motion by means of a rotating driving beam, a connection rod and a sliding body. In the present example, a flexible body is used for the connection rod. The sliding mass is not allowed to rotate and three revolute joints are used to connect the bodies. While each body has six degrees of freedom in space, the kinematical conditions lead to one degree of freedom for the whole system.

The motion of the mechanism can be viewed in the following gif animation

Concept

A body is usually considered to be a rigid or flexible part of a mechanical system (not to be confused with the human body). An example of a body is the arm of a robot, a wheel or axle in a car or the human forearm. A link is the connection of two or more bodies, or a body with the ground. The link is defined by certain (kinematical) constraints that restrict the relative motion of the bodies. Typical constraints are:

cardan joint or Universal Joint ; 4 kinematical constraints
prismatic joint; relative displacement along one axis is allowed, constrains relative rotation; implies 5 kinematical constraints
revolute joint; only one relative rotation is allowed; implies 5 kinematical constraints; see the example above
spherical joint; constrains relative displacements in one point, relative rotation is allowed; implies 3 kinematical constraints

There are two important terms in multibody systems: degree of freedom and constraint condition.

Degree of freedom

The degrees of freedom denote the number of independent kinematical possibilities to move. In other words, degrees of freedom are the minimum number of parameters required to completely define the position of an entity in space.

A rigid body has six degrees of freedom in the case of general spatial motion, three of them translational degrees of freedom and three rotational degrees of freedom. In the case of planar motion, a body has only three degrees of freedom with only one rotational and two translational degrees of freedom.

The degrees of freedom in planar motion can be easily demonstrated using a computer mouse. The degrees of freedom are: left-right, forward-backward and the rotation about the vertical axis.

Constraint condition

A constraint condition implies a restriction in the kinematical degrees of freedom of one or more bodies. The classical constraint is usually an algebraic equation that defines the relative translation or rotation between two bodies. There are furthermore possibilities to constrain the relative velocity between two bodies or a body and the ground. This is for example the case of a rolling disc, where the point of the disc that contacts the ground has always zero relative velocity with respect to the ground. In the case that the velocity constraint condition cannot be integrated in time in order to form a position constraint, it is called non-holonomic. This is the case for the general rolling constraint.

In addition to that there are non-classical constraints that might even introduce a new unknown coordinate, such as a sliding joint, where a point of a body is allowed to move along the surface of another body. In the case of contact, the constraint condition is based on inequalities and therefore such a constraint does not permanently restrict the degrees of freedom of bodies.

Equations of motion

The equations of motion are used to describe the dynamic behavior of a multibody system. Each multibody system formulation may lead to a different mathematical appearance of the equations of motion while the physics behind is the same. The motion of the constrained bodies is described by means of equations that result basically from Newton’s second law. The equations are written for general motion of the single bodies with the addition of constraint conditions. Usually the equations of motions are derived from the Newton-Euler equations or Lagrange’s equations.

The motion of rigid bodies is described by means of

\mathbf {M(q)} {\ddot {\mathbf {q} }}-\mathbf {Q} _{v}+\mathbf {C_{q}} ^{T}\mathbf {\lambda } =\mathbf {F} ,

(1)

\mathbf {C} (\mathbf {q} ,{\dot {\mathbf {q} }})=0

(2)

These types of equations of motion are based on so-called redundant coordinates, because the equations use more coordinates than degrees of freedom of the underlying system. The generalized coordinates are denoted by $\mathbf {q}$ , the mass matrix is represented by $\mathbf {M} (\mathbf {q} )$ which may depend on the generalized coordinates. $\mathbf {C}$ represents the constraint conditions and the matrix $\mathbf {C_{q}}$ (sometimes termed the Jacobian) is the derivative of the constraint conditions with respect to the coordinates. This matrix is used to apply constraint forces $\mathbf {\lambda }$ to the according equations of the bodies. The components of the vector $\mathbf {\lambda }$ are also denoted as Lagrange multipliers. In a rigid body, possible coordinates could be split into two parts,

$\mathbf {q} =\left[\mathbf {u} \quad \mathbf {\Psi } \right]^{T}$

where $\mathbf {u}$ represents translations and $\mathbf {\Psi }$ describes the rotations.

Quadratic velocity vector

In the case of rigid bodies, the so-called quadratic velocity vector $\mathbf {Q} _{v}$ is used to describe Coriolis and centrifugal terms in the equations of motion. The name is because $\mathbf {Q} _{v}$ includes quadratic terms of velocities and it results due to partial derivatives of the kinetic energy of the body.

Lagrange multipliers

The Lagrange multiplier $\lambda _{i}$ is related to a constraint condition $C_{i}=0$ and usually represents a force or a moment, which acts in “direction” of the constraint degree of freedom. The Lagrange multipliers do no "work" as compared to external forces that change the potential energy of a body.

Minimal coordinates

The equations of motion (1,2) are represented by means of redundant coordinates, meaning that the coordinates are not independent. This can be exemplified by the slider-crank mechanism shown above, where each body has six degrees of freedom while most of the coordinates are dependent on the motion of the other bodies. For example, 18 coordinates and 17 constraints could be used to describe the motion of the slider-crank with rigid bodies. However, as there is only one degree of freedom, the equation of motion could be also represented by means of one equation and one degree of freedom, using e.g. the angle of the driving link as degree of freedom. The latter formulation has then the minimum number of coordinates in order to describe the motion of the system and can be thus called a minimal coordinates formulation. The transformation of redundant coordinates to minimal coordinates is sometimes cumbersome and only possible in the case of holonomic constraints and without kinematical loops. Several algorithms have been developed for the derivation of minimal coordinate equations of motion, to mention only the so-called recursive formulation. The resulting equations are easier to be solved because in the absence of constraint conditions, standard time integration methods can be used to integrate the equations of motion in time. While the reduced system might be solved more efficiently, the transformation of the coordinates might be computationally expensive. In very general multibody system formulations and software systems, redundant coordinates are used in order to make the systems user-friendly and flexible.

References

J. Wittenburg, Dynamics of Systems of Rigid Bodies, Teubner, Stuttgart (1977).
J. Wittenburg, Dynamics of Multibody Systems, Berlin, Springer (2008).
K. Magnus, Dynamics of multibody systems, Springer Verlag, Berlin (1978).
P.E. Nikravesh, Computer-Aided Analysis of Mechanical Systems, Prentice-Hall (1988).
E.J. Haug, Computer-Aided Kinematics and Dynamics of Mechanical Systems, Allyn and Bacon, Boston (1989).
H. Bremer and F. Pfeiffer, Elastische Mehrkörpersysteme, B. G. Teubner, Stuttgart, Germany (1992).
J. García de Jalón, E. Bayo, Kinematic and Dynamic Simulation of Multibody Systems - The Real-Time Challenge, Springer-Verlag, New York (1994).
A.A. Shabana, Dynamics of multibody systems, Second Edition, John Wiley & Sons (1998).
M. Géradin, A. Cardona, Flexible multibody dynamics – A finite element approach, Wiley, New York (2001).
E. Eich-Soellner, C. Führer, Numerical Methods in Multibody Dynamics, Teubner, Stuttgart, 1998 (reprint Lund, 2008).
T. Wasfy and A. Noor, "Computational strategies for flexible multibody systems," ASME. Appl. Mech. Rev. 2003;56(6):553-613. doi:10.1115/1.1590354.

External links

http://real.uwaterloo.ca/~mbody/ Collected links of John McPhee

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.