McKelvey–Schofield chaos theorem

The McKelvey–Schofield chaos theorem is a result in social choice theory. It states that if preferences are defined over a multidimensional policy space, then majority rule is in general unstable: there is no Condorcet winner. Furthermore, any point in the space can be reached from any other point by a sequence of majority votes.

The theorem can be thought of as showing that Arrow's impossibility theorem holds when preferences are restricted to be concave in . The median voter theorem shows that when preferences are restricted to be single-peaked on the real line, Arrow's theorem does not hold, and the median voter's ideal point is a Condorcet winner. The chaos theorem shows that this good news does not continue in multiple dimensions.

Richard McKelvey initially proved the theorem for Euclidean preferences.[1] Norman Schofield extended the theorem to the more general class of concave preferences.[2]

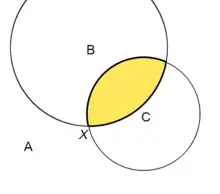
An example of the McKelvey-Schofield chaos theorem.

The figure shows an example. There are three voters in the electorate, with ideal points A, B and C. Voters prefer policies that are closer to them, i.e. they have circular indifference curves. The circles show B's and C's indifference curves through a policy X. If a candidate were to propose X, then the other candidate could beat him by proposing any point in the yellow area. This would be preferred by B and C. Any point in the plane will always have a set of points that are preferred by 2 out of 3 voters. In fact, you can get from any point to any other point by a series of majority votes.

References
  1. McKelvey, Richard D. (June 1976). "Intransitivities in Multidimensional Voting Models and Some Implications for Agenda Control". Journal of Economic Theory. 12 (3): 472–482. doi:10.1016/0022-0531(76)90040-5.
  2. Schofield, N. (1 October 1978). "Instability of Simple Dynamic Games". The Review of Economic Studies. 45 (3): 575–594. doi:10.2307/2297259.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.