Maclaurin spheroid

A Maclaurin spheroid is an oblate spheroid which arises when a self-gravitating fluid body of uniform density rotates with a constant angular velocity. This spheroid is named after the Scottish mathematician Colin Maclaurin, who formulated it for the shape of Earth in 1742.[1] In fact the figure of the Earth is far less oblate than Maclaurin's formula suggests, since the Earth is not homogeneous, but has a dense iron core. The Maclaurin spheroid is considered to be the simplest model of rotating ellipsoidal figures in equilibrium since it assumes uniform density.

Maclaurin formula

Angular velocity for Maclaurin spheroid

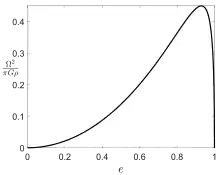
For a spheroid with equatorial semi-major axis ${\displaystyle a}$ and polar semi-minor axis ${\displaystyle c}$, the angular velocity ${\displaystyle \Omega }$ about ${\displaystyle c}$ is given by Maclaurin's formula[2]

${\displaystyle {\frac {\Omega ^{2}}{\pi G\rho }}={\frac {2{\sqrt {1-e^{2}}}}{e^{3}}}(3-2e^{2})\sin ^{-1}e-{\frac {6}{e^{2}}}(1-e^{2}),\quad e^{2}=1-{\frac {c^{2}}{a^{2}}},}$

where ${\displaystyle e}$ is the eccentricity of meridional cross-sections of the spheroid, ${\displaystyle \rho }$ is the density and ${\displaystyle G}$ is the gravitational constant. The formula predicts two possible equilibrium figures when ${\displaystyle \Omega \rightarrow 0}$, one is a sphere (${\displaystyle e\rightarrow 0}$) and the other is a very flattened spheroid (${\displaystyle e\rightarrow 1}$). The maximum angular velocity occurs at eccentricity ${\displaystyle e=0.92996}$ and its value is ${\displaystyle \Omega ^{2}/(\pi G\rho )=0.449331}$, so that above this speed, no equilibrium figures exist. The angular momentum ${\displaystyle L}$ is

${\displaystyle {\frac {L}{\sqrt {GM^{3}{\bar {a}}}}}={\frac {\sqrt {3}}{5}}\left({\frac {a}{\bar {a}}}\right)^{2}{\sqrt {\frac {\Omega ^{2}}{\pi G\rho }}}\ ,\quad {\bar {a}}=(a^{2}c)^{1/3}}$

where ${\displaystyle M}$ is the mass of the spheroid and ${\displaystyle {\bar {a}}}$ is the mean radius, the radius of a sphere of the same volume as the spheroid.

Stability

For a Maclaurin spheroid of eccentricity greater than 0.812670,[3] a Jacobi ellipsoid of the same angular momentum has lower total energy. If such a spheroid is composed of a viscous fluid, and if it suffers a perturbation which breaks its rotational symmetry, then it will gradually elongate into the Jacobi ellipsoidal form, while dissipating its excess energy as heat. This is termed secular instability. However, for a similar spheroid composed of an inviscid fluid, the perturbation will merely result in an undamped oscillation. This is described as dynamic (or ordinary) stability.

A Maclaurin spheroid of eccentricity greater than 0.952887[3] is dynamically unstable. Even if it is composed of an inviscid fluid and has no means of losing energy, a suitable perturbation will grow (at least initially) exponentially. Dynamic instability implies secular instability (and secular stability implies dynamic stability).[4]

See also

• Jacobi ellipsoid
• Spheroid
• Ellipsoid

References

1. Maclaurin, Colin. A Treatise of Fluxions: In Two Books. 1. Vol. 1. Ruddimans, 1742.
2. Chandrasekhar, Subrahmanyan. Ellipsoidal figures of equilibrium. Vol. 10. New Haven: Yale University Press, 1969.
3. Poisson, Eric; Will, Clifford (2014). Gravity: Newtonian, Post-Newtonian, Relativistic. Cambridge University Press. pp. 102–104. ISBN 978-1107032866.
4. Lyttleton, Raymond Arthur (1953). The Stability Of Rotating Liquid Masses. Cambridge University Press. ISBN 9781316529911.