Logic optimization

Logic optimization, a part of logic synthesis in electronics, is the process of finding an equivalent representation of the specified logic circuit under one or more specified constraints. Generally the circuit is constrained to minimum chip area meeting a prespecified delay.

Introduction

With the advent of logic synthesis, one of the biggest challenges faced by the electronic design automation (EDA) industry was to find the best netlist representation of the given design description. While two-level logic optimization had long existed in the form of the Quine–McCluskey algorithm, later followed by the Espresso heuristic logic minimizer, the rapidly improving chip densities, and the wide adoption of HDLs for circuit description, formalized the logic optimization domain as it exists today.

Today, logic optimization is divided into various categories:

Based on circuit representation

• Two-level logic optimization
• Multi-level logic optimization

Based on circuit characteristics

• Sequential logic optimization
• Combinational logic optimization

Based on type of execution

• Graphical optimization methods
• Tabular optimization methods
• Algebraic optimization methods

While a two-level circuit representation of circuits strictly refers to the flattened view of the circuit in terms of SOPs (sum-of-products) — which is more applicable to a PLA implementation of the design — a multi-level representation is a more generic view of the circuit in terms of arbitrarily connected SOPs, POSs (product-of-sums), factored form etc. Logic optimization algorithms generally work either on the structural (SOPs, factored form) or functional (BDDs, ADDs) representation of the circuit.

Two-level versus multi-level representations

If we have two functions F₁ and F₂:

${\displaystyle F_{1}=AB+AC+AD,\,}$

${\displaystyle F_{2}=A'B+A'C+A'E.\,}$

The above 2-level representation takes six product terms and 24 transistors in CMOS Rep.

A functionally equivalent representation in multilevel can be:

P = B + C.

F₁ = AP + AD.

F₂ = A'P + A'E.

While the number of levels here is 3, the total number of product terms and literals reduce because of the sharing of the term B + C.

Similarly, we distinguish between sequential and combinational circuits, whose behavior can be described in terms of finite-state machine state tables/diagrams or by Boolean functions and relations respectively.

Circuit minimization in Boolean algebra

In Boolean algebra, circuit minimization is the problem of obtaining the smallest logic circuit (Boolean formula) that represents a given Boolean function or truth table. For the case when the Boolean function is specified by a circuit (that is, we want to find an equivalent circuit of minimum size possible), the unbounded circuit minimization problem was long-conjectured to be ${\displaystyle \Sigma _{2}^{P}}$-complete, a result finally proved in 2008,[1] but there are effective heuristics such as Karnaugh maps and the Quine–McCluskey algorithm that facilitate the process.

Boolean function minimizing methods include:

• Blake–Poretsky method
• Nelson method[2][3][4][5][6]
• Quine method
• Quine–McCluskey method
• method of algebraic transformations
• Petrick's method
• Roth method[7]
• Kudielka method[8][9][10]
• Wells method[11]
• Scheinman's binary method[12][13]
• a method of minimizing functions in bases YES-NO and OR-NOT (Schaeffer and Pierce basis)
• method of undetermined coefficients
• hypercube method
• functional decomposition method
• Espresso heuristic logic minimizer

Purpose

The problem with having a complicated circuit (i.e. one with many elements, such as logic gates) is that each element takes up physical space in its implementation and costs time and money to produce in itself. Circuit minimization may be one form of logic optimization used to reduce the area of complex logic in integrated circuits.

Example

While there are many ways to minimize a circuit, this is an example that minimizes (or simplifies) a Boolean function. Note that the Boolean function carried out by the circuit is directly related to the algebraic expression from which the function is implemented.[14] Consider the circuit used to represent ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)}$. It is evident that two negations, two conjunctions, and a disjunction are used in this statement. This means that to build the circuit one would need two inverters, two AND gates, and an OR gate.

We can simplify (minimize) the circuit by applying logical identities or using intuition. Since the example states that A is true when B is false or the other way around, we can conclude that this simply means ${\displaystyle A\neq B}$. In terms of logical gates, inequality simply means an XOR gate (exclusive or). Therefore, ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)\iff A\neq B}$. Then the two circuits shown below are equivalent:

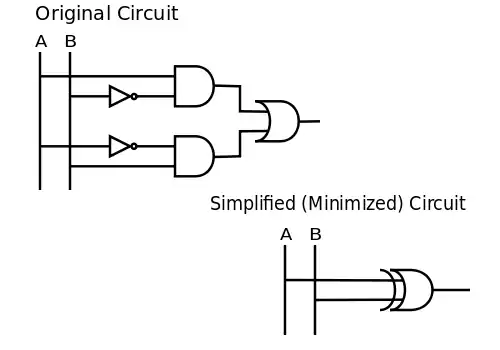
You can additionally check the correctness of the result using a truth table.

Graphical logic minimization methods

Graphical minimization methods for two-level logic include:

• Euler diagram
• Venn diagram
• Marquand diagram
• Harvard minimizing chart
• Veitch chart
• Karnaugh map
• Contact bones, contact grids (1955), and the triadic map by Antonín Svoboda
• Graphical method [15] [Вадим Николаевич Рогинский] (1913–1983)[16][17][18][19]
• Händler diagram
• Graph method (1965) by Herbert F. Kortum (1907–1979)[20][21][22][23][24][25][26][27][28][29]
• V diagram (2001) by Jonathan Westphal (1951–)[30][31]
• Majority-inverter graph
• Pandit plot

See also

• Binary decision diagram (BDD)
• Prime implicant
• Circuit complexity
• Function composition
• Function decomposition
• Gate underutilization

References

1. Buchfuhrer, David; Umans, Christopher (January 2011). "The complexity of Boolean formula minimization" (PDF). Journal of Computer and System Sciences (JCSS). Computer Science Department, California Institute of Technology, Pasadena, California, USA: Elsevier Inc. 77 (1): 142–153. doi:10.1016/j.jcss.2010.06.011. This is an extended version of the conference paper: Buchfuhrer, David; Umans, Christopher (2008). "The Complexity of Boolean Formula Minimization". Proceedings of Automata, Languages and Programming (PDF). 35th International Colloquium (ICALP). Lecture Notes in Computer Science (LNCS). 5125. Berlin / Heidelberg, Germany: Springer-Verlag. pp. 24–35. doi:10.1007/978-3-540-70575-8_3. ISBN 978-3-540-70574-1. Archived (PDF) from the original on 2018-01-14. Retrieved 2018-01-14.
2. Nelson, Raymond J. (June 1955). "Simplest Normal Truth Functions". Journal of Symbolic Logic. Association for Symbolic Logic. 20 (2): 105–108. doi:10.2307/2266893. JSTOR 2266893. (4 pages) (NB. A method converting a conjunctive normal form into a disjunctive normal form, followed by a procedure similar to Quine's.)
3. Nelson, Raymond J. (September 1955). "Weak Simplest Normal Truth Functions". Journal of Symbolic Logic. Association for Symbolic Logic. 20 (3): 232–234. doi:10.2307/2268219. JSTOR 2268219. (3 pages)
4. Lipp, Hans Martin; Becker, Jürgen (2011). Grundlagen der Digitaltechnik (in German) (reworked 7th ed.). Munich, Germany: Oldenbourg Wissenschaftsverlag GmbH / Walter de Gruyter. ISBN 9783486706932. ISBN 3486706934. Retrieved 2020-05-12. (316 pages)
5. Riznyk, Volodymyr; Solomko, Mykhailo (July 2017). "Minimization of Boolean functions by combinatorial method". Information and Control Systems: Mathematical Modeling (in English and Russian). 4/2 (36): 49–64. doi:10.15587/2312-8372.2017.108532. ISSN 2226-3780. UDC 681.325. Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
6. Riznyk, Volodymyr; Solomko, Mykhailo (July 2018). "Minimization of Conductive Normal Forms of Boolean Functions by Combinatorial Method" (PDF). Information and Control Systems: Mathematical Modeling (in English and Russian). 5/2 (43): 42–55. doi:10.15587/2312-8372.2018.146312. ISSN 2226-3780. UDC 681.325. Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
7. Roth, John Paul (November 1960). "Minimization over Boolean Trees". IBM Journal of Research and Development. 4 (5): 543–558. doi:10.1147/rd.45.0543. eISSN 0018-8646. ISSN 0018-8646.
8. Kudielka, Viktor; Walk, Kurt; Bandat, Kurt; Lucas, Peter; Zemanek, Heinrich "Heinz" Josef (1960-02-29). "4–5". In Zemanek, Heinrich "Heinz" Josef (ed.). Programs for Logical Data Processing. Mailüfterl (Final report). Vienna, Austria: Technical University of Vienna, Institut für Nachrichtentechnik. European Research Office Contract DA-91-591-EC-1062. Retrieved 2020-05-29. (198 pages)
9. Kudielka, Viktor; Lucas, Peter; Walk, Kurt; Bandat, Kurt; Bekic, Heinz; Zemanek, Heinrich "Heinz" Josef (1961-07-31). "2". Extension of the Algorithmic Language ALGOL (Final Report). European Research Office Contract DA-91–591-EUC-1430.
10. Kudielka, Viktor (January 1963) [1961-10-18]. "Programmierung von Minimisierungsverfahren für zweistufige Logik". In Dörr, Johannes; Peschl, Ernst Ferdinand; Unger, Heinz (eds.). 2. Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 18. bis 20. Oktober 1961 in Saarbrücken. Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 4 (2013-12-20 reprint of 1st ed.). Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. pp. 49–65. doi:10.1007/978-3-0348-4156-6. ISBN 978-3-0348-4081-1. Retrieved 2020-04-15. (152 pages)
11. Wells, Mark B. (1962). "Chapter 14. Switching Theory: Application of a Finite Set Covering Theorem to the Simplification of Boolean Function Expressions". Information Processing, Proceedings of the 2nd IFIP Congress 1962, Munich, Germany, August 27 - September 1, 1962. 2. Munich, Germany: North-Holland. pp. 731–735. Retrieved 2020-05-28.
12. Scheinman, Arnold H. (July 1962) [1962-03-06]. "A Method For Simplifying Boolean Functions". Bell System Technical Journal. Nokia Bell Labs. 41 (4): 1337–1346. doi:10.1002/j.1538-7305.1962.tb03280.x. ISSN 0005-8580. (NB. Also known as Scheinman's binary method, this is an easy to use iterative method also for large functions, which will result in significantly simplified functions, but not necessarily in the simplest. The author is sometimes misspelled as "Schienmann".)
13. Föllinger, Otto; Weber, Wolfgang (1967) [June 1965]. "5.4. Die Methode der Harvard Group of Computation / 5.5 Vereinfachungsmethode nach Scheinman". Written at Frankfurt am Main, Germany. Methoden der Schaltalgebra (in German) (1 ed.). Munich, Germany: R. Oldenbourg Verlag. pp. 103, 120, 122–128, 128–135. (6+320+6 pages)
14. Mano, M. Morris; Kime, Charles R. (2014). Logic and Computer Design Fundamentals (4th new international ed.). Pearson Education Limited. p. 54. ISBN 978-1-292-02468-4.
15. Вадим Николаевич Рогинский (некролог) [Vadim Nikolaevich Roginsky (obituary)]. Problemy Peredachi Informatsii Проблемы передачи информации [Problems of Information Transmission] (in Russian). XIX (3): 111. 1983. ISSN 0555-2923. Mi ppi1195. Archived from the original on 2020-05-29. Retrieved 2020-05-29. (NB. The author's (GND 1157173993, 1158776373) name is sometimes translated as "Vladimir Nikolaevič", "Wladimir Nikolajewitsch" and as "Roginsky", "Roginskiĭ", or "Roginski".)
16. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1957). "(unknown)" [Graphical method of synthesizing contact networks]. Èlektrosvâzʹ (in Russian). XI (11): 82–88. ISSN 0013-5771. Cite uses generic title (help)
17. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1959) [1957-03-29]. "A graphical method for the synthesis of multi-terminal contact networks". Proceedings of an International Symposium on the Theory of Switching, 2–5 April 1957, Part II. The Annals of the Computation Laboratory of Harvard University. XXX. Harvard University, Cambridge, Massachusetts, USA. pp. 302–315. (345 pages) (NB. This is a translation of a Russian paper prepared for the symposium. Roginskij submitted the paper for presentation, but then could not attend personally. The translation was carried out by some of the American attendees.)
18. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1958). Povarov [Поваров], Gellius Nikolaevich [Геллий Николаевич] (ed.). "(unknown)" [Graphical method for synthesizing multi-terminal contact networks]. Avtomatika [Automation] (in Russian). Kiev. 3: 84–91. ISSN 0572-2691. Cite uses generic title (help)
19. Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1962). Grundlagen der Struktursynthese von Relaisschaltungen (in German). Translated by Hausenblas, Albin; Pfaffinger, Robert; Resele, H. (1st German ed.). Munich, Germany: R. Oldenbourg Verlag. OCLC 968499019. OCLC 163791522. Retrieved 2002-05-30 (204 pages). This book is a translation of the original work: Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1959). Kharkevich [Харкевич], Aleksandr Aleksandrovich [Александр Александрович] (ed.). Ėlementy strukturnogo sinteza releĭnykh skhem upravlenii︠a︡ Элементы структурного синтеза релейных схем управления (in Russian) (1st ed.). Moscow: Изд-во Академии наук СССР (Izdatel'stvo akademii nauk SSSR) . Also available in English as: Roginskij [Рогинский], Vadim Nikolaevich [Вадим Николаевич] (1963). The synthesis of relay switching circuits. Translated by Chrzczonowicz (1st English ed.). New York, USA: Van Nostrand Reinhold Inc. ISBN 0-44207020-9. (188 pages).
20. Kortum, Herbert Franz (1965). "Minimierung von Kontaktschaltungen durch Kombination von Kürzungsverfahren und Graphenmethoden" [Minimization of contact circuits by combination of reduction procedures and graphical methods]. messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 8 (12): 421–425. ISSN 0026-0347. OCLC 310970250. CODEN MSRGAN, MSRGA, MMSRD. DNB-IDN 01269357X. ZDB-ID 512087-1. Retrieved 2020-11-04. (5 pages)
21. Kortum, Herbert Franz (1966). "Konstruktion und Minimierung von Halbleiterschaltnetzwerken mittels Graphentransformation". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (1): 9–12. ISSN 0026-0347. OCLC 310970250. CODEN MSRGAN, MSRGA, MMSRD. DNB-IDN 01269357X. ZDB-ID 512087-1. Retrieved 2018-06-17.
22. Kortum, Herbert Franz (1966). "Weitere Bemerkungen zur Minimierung von Schaltnetzwerken mittels Graphenmethoden". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (3): 96–102. ISSN 0026-0347. OCLC 310970250. CODEN MSRGAN, MSRGA, MMSRD. DNB-IDN 01269357X. ZDB-ID 512087-1. Retrieved 2018-06-17.
23. Kortum, Herbert Franz (1965). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen" [Further remarks on treatment of switching networks by means of graphs]. Regelungstechnik (Conference paper). 10. Internationales Wissenschaftliches Kolloquium. [10th international scientific colloquium] (in German). Technische Hochschule Ilmenau. 10 (5): 33–39. Retrieved 2020-11-04 (7 pages); Kortum, Herbert Franz (1966). "Weitere Bemerkungen zur Behandlung von Schaltnetzwerken mittels Graphen. Konstruktion von vermaschten Netzwerken (Brückenschaltungen)" [Further remarks on treatment of switching networks by means of graphs]. messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 9 (5): 151–157. ISSN 0026-0347. OCLC 310970250. CODEN MSRGAN, MSRGA, MMSRD. DNB-IDN 01269357X. ZDB-ID 512087-1.
24. Kortum, Herbert Franz (1967). "Über zweckmäßige Anpassung der Graphenstruktur diskreter Systeme an vorgegebene Aufgabenstellungen". messen-steuern-regeln (msr) (in German). Berlin / Leipzig, Germany: VEB Verlag Technik. 10 (6): 208–211. ISSN 0026-0347. OCLC 310970250. CODEN MSRGAN, MSRGA, MMSRD. DNB-IDN 01269357X. ZDB-ID 512087-1.
25. Kortum, Herbert Franz (1966) [1965]. "Zur Minimierung von Schaltsystemen" [Minimization of switching circuits]. Wissenschaftliche Zeitschrift der TU Ilmenau (in German). Jena, Germany: Technische Hochschule für Elektrotechnik Ilmenau / Forschungsstelle für Meßtechnik und Automatisierung der Deutschen Akademie der Wissenschaften. 12 (2): 181–186. Retrieved 2020-11-04. (6 pages)
26. Tafel, Hans Jörg (1971). "4.3.5. Graphenmethode zur Vereinfachung von Schaltfunktionen". Written at RWTH, Aachen, Germany. Einführung in die digitale Datenverarbeitung [Introduction to digital information processing] (in German). Munich, Germany: Carl Hanser Verlag. pp. 98–105, 107–113. ISBN 3-446-10569-7.
27. Axmann, Hans-Peter (2019) [1979-06-13]. Einführung in die technische Informatik: Funktionsweise digitaler Bausteine und deren Verwendung in Datenerfassungssystemen (in German) (reprint of 1st ed.). Springer-Verlag Wien GmbH. p. 37. doi:10.1007/978-3-7091-4478-7. ISBN 978-3-211-81546-5. Retrieved 2020-04-15. p. 37: […] Die Graphenmethode zur Vereinfachung von Schaltfunktionen zeichnet sich durch besondere Anschaulichkeit und Einfachheit aus. Sie ist dann besonders vorteilhaft, wenn die Schaltfunktion unter Verwendung bestimmter Verknüpfungsglieder mit minimalem Aufwand an Bauelementen und Verbindungsleitungen zu realisieren ist. Sie ist anderen Methoden, besonders bei der Netzwerksynthese von Brückenschaltungen wie auch bei der Optimierung von Kontaktschaltungen mit Sperrdioden, überlegen. Die erfolgreiche Anwendung der Graphenmethode setzt voraus, daß die vorgegebene Funktion bereits in einer weitgehend vereinfachten Form vorliegt, da mit dieser Methode Redundanzen nur noch sehr schwer zu eliminieren sind. […] (290 pages)
28. Winkler, Jürgen F. H. (2013-04-07) [2008-10-25]. "Die Oprema – der Relaisrechner des Zeisswerks Jena" (PDF) (Lecture notes) (in German). Friedrich Schiller University, Jena, Germany. pp. 1–27. Archived from the original (PDF) on 2017-08-30. (27 pages)
29. Winkler, Jürgen F. H. (2019-08-26) [2014-10-25]. "Oprema – The Relay Computer of Carl Zeiss Jena" (PDF). 1. Friedrich Schiller University, Jena, Germany. pp. 1–33. arXiv:1908.09549. Archived (PDF) from the original on 2020-09-29. Retrieved 2020-11-04. (33 pages)
30. Westphal, Jonathan (2007-08-07) [2001-10-05, 2000-10-06]. "Devices and techniques for logical processing" (PDF). Patent US7254304B2. Archived (PDF) from the original on 2020-05-09. Retrieved 2020-05-09. (77 pages)
31. Westphal, Jonathan; Hardy, Jim (2005-10-01) [2004-02-16]. "Logic as a Vector System". Journal of Logic and Computation. Idaho State University, Pocatello, Idaho, USA: Oxford University Press. 15 (5): 751–765. doi:10.1093/logcom/exi040. Archived from the original on 2020-05-09. Retrieved 2020-05-09. (15 pages)

Further reading

• Hwa, "Sherman" Hsuen Ren (June 1974). "A Method of Generating Prime Implicants of a Boolean Expression". IEEE Transactions on Computers. IEEE. C-23 (6): 637–641. doi:10.1109/T-C.1974.224003. eISSN 1557-9956. ISSN 0018-9340. S2CID 10646917. 1F09. Retrieved 2020-05-12; Hwa, "Sherman" Hsuen Ren (April 1973). A Method of Generating Prime Implicants of a Boolean Expression. Basser Department of Computer Science, University of Sydney. Technical Report 82.
• Lind, Larry Frederick; Nelson, John Christopher Cunliffe (1977). Analysis and Design of Sequential Digital Systems. Macmillan Press. ISBN 0-33319266-4. (146 pages)
• Ghosh, Debidas (June 1977) [1977-01-21]. "A method of generating prime factors of a Boolean Expression in a conjunctive normal form with the possibility of inclusion of Don't care combination" (PDF). Journal of Technology. Department of Mathematics, Bengal Engineering College, Howrah, India. XXII (1). Archived (PDF) from the original on 2020-05-12. Retrieved 2020-05-12.
• De Micheli, Giovanni (1994). Synthesis and Optimization of Digital Circuits. McGraw-Hill. ISBN 0-07-016333-2. (NB. Chapters 7–9 cover combinatorial two-level, combinatorial multi-level, and respectively sequential circuit optimization.)
• Hachtel, Gary D.; Somenzi, Fabio (2006) [1996]. Logic Synthesis and Verification Algorithms. Springer Science & Business Media. ISBN 978-0-387-31005-3.
• Kohavi, Zvi; Jha, Niraj K. (2009). "4–6". Switching and Finite Automata Theory (3rd ed.). Cambridge University Press. ISBN 978-0-521-85748-2.
• Knuth, Donald Ervin (2010). "7.1.2: Boolean Evaluation". The Art of Computer Programming. 4A. Addison-Wesley. pp. 96–133. ISBN 978-0-201-03804-0.
• Rutenbar, Rob A. Multi-level minimization, Part I: Models & Methods (PDF) (lecture slides). Carnegie Mellon University (CMU). Lecture 7. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15; Rutenbar, Rob A. Multi-level minimization, Part II: Cube/Cokernel Extract (PDF) (lecture slides). Carnegie Mellon University (CMU). Lecture 8. Archived (PDF) from the original on 2018-01-15. Retrieved 2018-01-15.
• Tomaszewski, Sebastian P.; Celik, Ilgaz U.; Antoniou, George E. (December 2003) [2003-03-05, 2002-04-09]. "WWW-based Boolean function minimization" (PDF). International Journal of Applied Mathematics and Computer Science. 13 (4): 577–584. Archived (PDF) from the original on 2020-05-10. Retrieved 2020-05-10. (7 pages)
• Wilhelmy, Alexander; Kudielka, Viktor; Deussen, Peter; Böhling, Karl Heinz; Händler, Wolfgang; Neander, Joachim (January 1963) [1961-10-18]. Dörr, Johannes; Peschl, Ernst Ferdinand; Unger, Heinz (eds.). 2. Colloquium über Schaltkreis- und Schaltwerk-Theorie - Vortragsauszüge vom 18. bis 20. Oktober 1961 in Saarbrücken. Internationale Schriftenreihe zur Numerischen Mathematik [International Series of Numerical Mathematics] (ISNM) (in German). 4 (2013-12-20 reprint of 1st ed.). Institut für Angewandte Mathematik, Universität Saarbrücken, Rheinisch-Westfälisches Institut für Instrumentelle Mathematik: Springer Basel AG / Birkhäuser Verlag Basel. doi:10.1007/978-3-0348-4156-6. ISBN 978-3-0348-4081-1. Retrieved 2020-04-15. (152 pages)
• Brayton, Robert King; Rudell, Richard L.; Sangiovanni-Vincentelli, Alberto Luigi; Wang, Albert R. (December 1987). "MIS: A Multiple-Level Logic Optimization System". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 6 (6): 1062–1081. doi:10.1109/TCAD.1987.1270347. (MIS)
• De Geus, Aart J.; Cohen, William W. (1985). "A Rule-Based System for Optimizing Combinational Logic". IEEE Design & Test of Computers. 2 (4): 22–32. doi:10.1109/MDT.1985.294719. S2CID 46651690. (SOCRATES)
• Khatri, Sunil P.; Gulati, Kanupriya, eds. (2011). Advanced Techniques in Logic Synthesis, Optimizations and Applications (1 ed.). New York / Dordrecht / Heidelberg / London: Springer Science+Business Media, LLC. ISBN 978-1-4419-7517-1. (xxii+423+1 pages)