Local nonsatiation
The property of local nonsatiation of consumer preferences states that for any bundle of goods there is always another bundle of goods arbitrarily close that is preferred to it.[1]
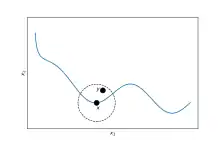
Illustration of preferences that are locally nonsatiated but not strongly monotonic.
Formally, if X is the consumption set, then for any and every , there exists a such that and is preferred to .
Several things to note are:
- Local nonsatiation is implied by monotonicity of preferences. However, as the converse is not true, local nonsatiation is a weaker condition.
- There is no requirement that the preferred bundle y contain more of any good – hence, some goods can be "bads" and preferences can be non-monotone.
- It rules out the extreme case where all goods are "bads", since the point x = 0 would then be a bliss point.
- Local nonsatiation can only occur either if the consumption set is unbounded or open (in other words, it is not compact) or if x is on a section of a bounded consumption set sufficiently far away from the ends. Near the ends of a bounded set, there would necessarily be a bliss point where local nonsatiation does not hold.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.