Kittell graph
In the mathematical field of graph theory, the Kittell graph is a planar graph with 23 vertices and 63 edges. Its unique planar embedding has 42 triangular faces.[1] The Kittell graph is named after Irving Kittell, who used it as a counterexample to Alfred Kempe's flawed proof of the four-color theorem.[2] Simpler counterexamples include the Errera graph and Poussin graph (both published earlier than Kittell) and the Fritsch graph and Soifer graph.
| Kittel graph | |
|---|---|
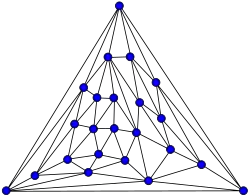 The Kittell graph | |
| Vertices | 23 |
| Edges | 63 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 3 |
| Table of graphs and parameters | |
References
- Weisstein, Eric W. "Kittell Graph". MathWorld.
- Kittell, Irving (1935), "A group of operations on a partially colored map", Bulletin of the American Mathematical Society, 41 (6): 407–413, doi:10.1090/S0002-9904-1935-06104-X, MR 1563103
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.