Kaleidocycle

A kaleidocycle (or flextangle) is a paper-folded model connecting 6 tetrahedra (or disphenoids) on opposite edges into a cycle. If the faces of the disphenoids are equilateral triangles It can be constructed from a stretched triangular tiling net with 4 triangles in one direction and an even number in the other direction.

Regular-based right pyramids

6 tetrahedra where vertices meet at the center. Blue edges are doubled with pairs of faces hidden.
Faces24 isosceles triangles
Edges36 (6 as degenerate pairs)
Vertices12
Symmetry groupC3v, [3], (*33), order 6
Propertiestorus

Net
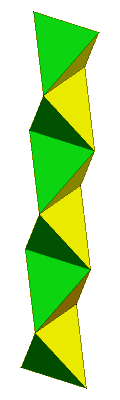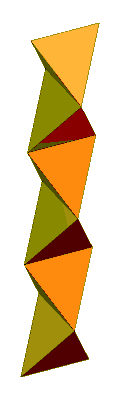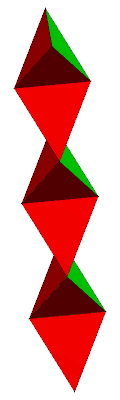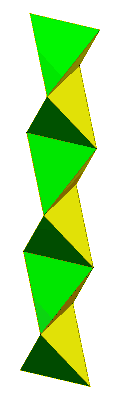
A kaleidocycle before it is wrapped into a ring makes a chain of 6 disphenoids connected edge to edge.

The model represents a flexible polyhedron (having degenerate pairs of coinciding edges in transition) that can be twisted around a ring axis, showing 4 sets of 6 triangle faces that can be drawn with different colors or patterns.

Example

A kaleidocycle using disphenoids with scalene triangle faces. Each hinge connects a disphenoid with its chiral partner. The corresponding net hence exhibits reflectional symmetry.

Variations

Beyond 6 sides, higher even number of tetrahedra, 8, 10, 12, etc, can be chained together. These models will leave a central gap, depending on the proportions of the triangle faces.[1]

History

Wallace Walker coined the word kaleidocycle in the 1950s from the Greek kalos (beautiful), eidos (form), and kyklos (ring).

In 1977 Doris Schattschneider and Wallace Walker published a book about them using M.C. Escher patterns.[2][3]

Cultural uses

It was called a flextangle as a prop in the 2018 film A Wrinkle in Time, with its inner faces colored with hearts and patterns which hidden when those faces are folded together. The paper toy suggested how space and time could be folded to explain the magical travels of the story. The toy is given to the daughter by her father at the start of the movie and its hearts show how love can be enfolded and still there, even after the father mysteriously disappears.[4]

See also

References
  1. regular tetrahedra solutions, 8, 10, 12 with Mathematica
  2. Book Review:Art Meets Math in 'Kaleidocycles' May 27, 1988
  3. Doris Schattschneider and Walker, M.C. Escher Kaleidocycles, 1977. ISBN 0-906212-28-6.
  4. Cooper, Meghan (March 8, 2018). "Disney's A Wrinkle in Time Kaleidocycle Flextangle and Activity Printables". Jamonkey. Retrieved October 15, 2018.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.