History of mathematical notation

The history of mathematical notation[1] includes the commencement, progress, and cultural diffusion of mathematical symbols and the conflict of the methods of notation confronted in a notation's move to popularity or inconspicuousness. Mathematical notation[2] comprises the symbols used to write mathematical equations and formulas. Notation generally implies a set of well-defined representations of quantities and symbols operators.[3] The history includes Hindu–Arabic numerals, letters from the Roman, Greek, Hebrew, and German alphabets, and a host of symbols invented by mathematicians over the past several centuries.

The development of mathematical notation can be divided in stages.[4][5] The "rhetorical" stage is where calculations are performed by words and no symbols are used.[6] The "syncopated" stage is where frequently used operations and quantities are represented by symbolic syntactical abbreviations. From ancient times through the post-classical age,[note 1] bursts of mathematical creativity were often followed by centuries of stagnation. As the early modern age opened and the worldwide spread of knowledge began, written examples of mathematical developments came to light. The "symbolic" stage is where comprehensive systems of notation supersede rhetoric. Beginning in Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day. This symbolic system was in use by medieval Indian mathematicians and in Europe since the middle of the 17th century,[7] and has continued to develop in the contemporary era.

The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, the focus here, the investigation into the mathematical methods and notation of the past.

Rhetorical stage

Although the history commences with that of the Ionian schools, there is no doubt that those Ancient Greeks who paid attention to it were largely indebted to the previous investigations of the Ancient Egyptians and Ancient Phoenicians. Numerical notation's distinctive feature, i.e. symbols having local as well as intrinsic values (arithmetic), implies a state of civilization at the period of its invention. Our knowledge of the mathematical attainments of these early peoples, to which this section is devoted, is imperfect and the following brief notes be regarded as a summary of the conclusions which seem most probable, and the history of mathematics begins with the symbolic sections.

Many areas of mathematics began with the study of real world problems, before the underlying rules and concepts were identified and defined as abstract structures. For example, geometry has its origins in the calculation of distances and areas in the real world; algebra started with methods of solving problems in arithmetic.

There can be no doubt that most early peoples which have left records knew something of numeration and mechanics, and that a few were also acquainted with the elements of land-surveying. In particular, the Egyptians paid attention to geometry and numbers, and the Phoenicians to practical arithmetic, book-keeping, navigation, and land-surveying. The results attained by these people seem to have been accessible, under certain conditions, to travelers. It is probable that the knowledge of the Egyptians and Phoenicians was largely the result of observation and measurement, and represented the accumulated experience of many ages.

Beginning of notation

Written mathematics began with numbers expressed as tally marks, with each tally representing a single unit. The numerical symbols consisted probably of strokes or notches cut in wood or stone, and intelligible alike to all nations.[note 2] For example, one notch in a bone represented one animal, or person, or anything else. The peoples with whom the Greeks of Asia Minor (amongst whom notation in western history begins) were likely to have come into frequent contact were those inhabiting the eastern littoral of the Mediterranean: and Greek tradition uniformly assigned the special development of geometry to the Egyptians, and that of the science of numbers[note 3] either to the Egyptians or to the Phoenicians.

The Ancient Egyptians had a symbolic notation which was the numeration by Hieroglyphics.[8][9] The Egyptian mathematics had a symbol for one, ten, one-hundred, one-thousand, ten-thousand, one-hundred-thousand, and one-million. Smaller digits were placed on the left of the number, as they are in Hindu–Arabic numerals. Later, the Egyptians used hieratic instead of hieroglyphic script to show numbers. Hieratic was more like cursive and replaced several groups of symbols with individual ones. For example, the four vertical lines used to represent four were replaced by a single horizontal line. This is found in the Rhind Mathematical Papyrus (c. 2000–1800 BC) and the Moscow Mathematical Papyrus (c. 1890 BC). The system the Egyptians used was discovered and modified by many other civilizations in the Mediterranean. The Egyptians also had symbols for basic operations: legs going forward represented addition, and legs walking backward to represent subtraction.

The Mesopotamians had symbols for each power of ten.[10] Later, they wrote their numbers in almost exactly the same way done in modern times. Instead of having symbols for each power of ten, they would just put the coefficient of that number. Each digit was separated by only a space, but by the time of Alexander the Great, they had created a symbol that represented zero and was a placeholder. The Mesopotamians also used a sexagesimal system, that is base sixty. It is this system that is used in modern times when measuring time and angles. Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s.[11] Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework. The earliest evidence of written mathematics dates back to the ancient Sumerians and the system of metrology from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.[12]

The majority of Mesopotamian clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular, reciprocal and pairs.[13] The tablets also include multiplication tables and methods for solving linear and quadratic equations. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places. Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this derives the modern-day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 × 6) degrees in a circle, as well as the use of minutes and seconds of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors: the reciprocal of any integer which is a multiple of divisors of 60 has a finite expansion in base 60. (In decimal arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.) Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.

Syncopated stage

Archimedes Thoughtful
by Fetti (1620)

---

The last words attributed to Archimedes are "Do not disturb my circles",[note 4] a reference to the circles in the mathematical drawing that he was studying when disturbed by the Roman soldier.

The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks, but the subsequent history may be divided into periods, the distinctions between which are tolerably well marked. Greek mathematics, which originated with the study of geometry, tended from its commencement to be deductive and scientific. Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides.[note 5] The ancient mathematical texts are available with the prior mentioned Ancient Egyptians notation and with Plimpton 322 (Babylonian mathematics c. 1900 BC). The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction".[14]

Plato's influence has been especially strong in mathematics and the sciences. He helped to distinguish between pure and applied mathematics by widening the gap between "arithmetic", now called number theory and "logistic", now called arithmetic. Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics.[15] Aristotle is credited with what later would be called the law of excluded middle.

Abstract Mathematics[16] is what treats of magnitude[note 6] or quantity, absolutely and generally conferred, without regard to any species of particular magnitude, such as arithmetic and geometry, In this sense, abstract mathematics is opposed to mixed mathematics, wherein simple and abstract properties, and the relations of quantities primitively considered in mathematics, are applied to sensible objects, and by that means become intermixed with physical considerations, such as in hydrostatics, optics, and navigation.[16]

Archimedes is generally considered to be the greatest mathematician of antiquity and one of the greatest of all time.[17][18] He used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, and gave a remarkably accurate approximation of pi.[19] He also defined the spiral bearing his name, formulae for the volumes of surfaces of revolution and an ingenious system for expressing very large numbers.

Euclid's Elements

---

The prop. 31, 32 and 33 of the book of Euclid XI, which is located in vol. 2 of the manuscript, the sheets 207 to – 208 recto.

In the historical development of geometry, the steps in the abstraction of geometry were made by the ancient Greeks. Euclid's Elements being the earliest extant documentation of the axioms of plane geometry— though Proclus tells of an earlier axiomatisation by Hippocrates of Chios.[20] Euclid's Elements (c. 300 BC) is one of the oldest extant Greek mathematical treatises[note 7] and consisted of 13 books written in Alexandria; collecting theorems proven by other mathematicians, supplemented by some original work.[note 8] The document is a successful collection of definitions, postulates (axioms), propositions (theorems and constructions), and mathematical proofs of the propositions. Euclid's first theorem is a lemma that possesses properties of prime numbers. The influential thirteen books cover Euclidean geometry, geometric algebra, and the ancient Greek version of algebraic systems and elementary number theory. It was ubiquitous in the Quadrivium and is instrumental in the development of logic, mathematics, and science.

Diophantus of Alexandria was author of a series of books called Arithmetica, many of which are now lost. These texts deal with solving algebraic equations. Boethius provided a place for mathematics in the curriculum in the 6th century when he coined the term quadrivium to describe the study of arithmetic, geometry, astronomy, and music. He wrote De institutione arithmetica, a free translation from the Greek of Nicomachus's Introduction to Arithmetic; De institutione musica, also derived from Greek sources; and a series of excerpts from Euclid's Elements. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.[21][22]

Acrophonic and Milesian numeration

The Greeks employed Attic numeration,[23] which was based on the system of the Egyptians and was later adapted and used by the Romans. Greek numerals one through four were vertical lines, as in the hieroglyphics. The symbol for five was the Greek letter Π (pi), which is the letter of the Greek word for five, pente. Numbers six through nine were pente with vertical lines next to it. Ten was represented by the letter (Δ) of the word for ten, deka, one hundred by the letter from the word for hundred, etc.

The Ionian numeration used their entire alphabet including three archaic letters. The numeral notation of the Greeks, though far less convenient than that now in use, was formed on a perfectly regular and scientific plan,[24] and could be used with tolerable effect as an instrument of calculation, to which purpose the Roman system was totally inapplicable. The Greeks divided the twenty-four letters of their alphabet into three classes, and, by adding another symbol to each class, they had characters to represent the units, tens, and hundreds. (Jean Baptiste Joseph Delambre's Astronomie Ancienne, t. ii.)

Α (α)	Β (β)	Г (γ)	Δ (δ)	Ε (ε)	Ϝ (ϝ)	Ζ (ζ)	Η (η)	θ (θ)	Ι (ι)	Κ (κ)	Λ (λ)	Μ (μ)	Ν (ν)	Ξ (ξ)	Ο (ο)	Π (π)	Ϟ (ϟ)	Ρ (ρ)	Σ (σ)	Τ (τ)	Υ (υ)	Φ (φ)	Χ (χ)	Ψ (ψ)	Ω (ω)	Ϡ (ϡ)
1	2	3	4	5	6	7	8	9	10	20	30	40	50	60	70	80	90	100	200	300	400	500	600	700	800	900

This system appeared in the third century BC, before the letters digamma (Ϝ), koppa (Ϟ), and sampi (Ϡ) became obsolete. When lowercase letters became differentiated from upper case letters, the lower case letters were used as the symbols for notation. Multiples of one thousand were written as the nine numbers with a stroke in front of them: thus one thousand was ",α", two-thousand was ",β", etc. M (for μὐριοι, as in "myriad") was used to multiply numbers by ten thousand. For example, the number 88,888,888 would be written as M,ηωπη*ηωπη[25]

Greek mathematical reasoning was almost entirely geometric (albeit often used to reason about non-geometric subjects such as number theory), and hence the Greeks had no interest in algebraic symbols. The great exception was Diophantus of Alexandria, the great algebraist.[26] His Arithmetica was one of the texts to use symbols in equations. It was not completely symbolic, but was much more so than previous books. An unknown number was called s.[27] The square of s was ${\displaystyle \Delta ^{y}}$; the cube was ${\displaystyle K^{y}}$; the fourth power was ${\displaystyle \Delta ^{y}\Delta }$; and the fifth power was ${\displaystyle \Delta K^{y}}$.[28][note 9]

Chinese mathematical notation

The numbers 0–9 in Chinese huāmǎ (花碼) numerals

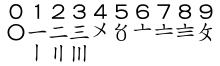
The Chinese used numerals that look much like the tally system.[29] Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the Roman numeral for ten. Nowadays, the huāmǎ system is only used for displaying prices in Chinese markets or on traditional handwritten invoices.

In the history of the Chinese, there were those who were familiar with the sciences of arithmetic, geometry, mechanics, optics, navigation, and astronomy. Mathematics in China emerged independently by the 11th century BC.[30] It is almost certain that the Chinese were acquainted with several geometrical or rather architectural implements;[note 10] with mechanical machines;[note 11] that they knew of the characteristic property of the magnetic needle; and were aware that astronomical events occurred in cycles. Chinese of that time had made attempts to classify or extend the rules of arithmetic or geometry which they knew, and to explain the causes of the phenomena with which they were acquainted beforehand. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry.

Counting rod numerals

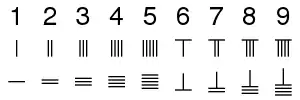
Chinese mathematics made early contributions, including a place value system.[31][32] The geometrical theorem known to the ancient Chinese were acquainted was applicable in certain cases (namely the ratio of sides).[note 12] It is that geometrical theorems which can be demonstrated in the quasi-experimental way of superposition were also known to them. In arithmetic their knowledge seems to have been confined to the art of calculation by means of the swan-pan, and the power of expressing the results in writing. Our knowledge of the early attainments of the Chinese, slight though it is, is more complete than in the case of most of their contemporaries. It is thus instructive, and serves to illustrate the fact, that it can be known a nation may possess considerable skill in the applied arts with but our knowledge of the later mathematics on which those arts are founded can be scarce. Knowledge of Chinese mathematics before 254 BC is somewhat fragmentary, and even after this date the manuscript traditions are obscure. Dates centuries before the classical period are generally considered conjectural by Chinese scholars unless accompanied by verified archaeological evidence.

As in other early societies the focus was on astronomy in order to perfect the agricultural calendar, and other practical tasks, and not on establishing formal systems. The Chinese Board of Mathematics duties were confined to the annual preparation of an almanac, the dates and predictions in which it regulated. Ancient Chinese mathematicians did not develop an axiomatic approach, but made advances in algorithm development and algebra. The achievement of Chinese algebra reached its zenith in the 13th century, when Zhu Shijie invented method of four unknowns.

As a result of obvious linguistic and geographic barriers, as well as content, Chinese mathematics and that of the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently up to the time when The Nine Chapters on the Mathematical Art reached its final form, while the Writings on Reckoning and Huainanzi are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory. The Pythagorean theorem for example, has been attested to the time of the Duke of Zhou. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal,[33] such as by Shen Kuo.

Modern artist's impression of Shen Kuo.

The state of trigonometry in China slowly began to change and advance during the Song Dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations.[34] The polymath Chinese scientist, mathematician and official Shen Kuo (1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs.[34] Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231–1316).[35] As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry in his calculations to improve the calendar system and Chinese astronomy.[36][37] The mathematical science of the Chinese would incorporate the work and teaching of Arab missionaries with knowledge of spherical trigonometry who had come to China in the course of the thirteenth century.

Indian & Arabic numerals and notation

Although the origin of our present system of numerical notation is ancient, there is no doubt that it was in use among the Hindus over two thousand years ago. The algebraic notation of the Indian mathematician, Brahmagupta, was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend (the number to be subtracted), and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms.[38] The Hindu–Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics.[39][40]

A page from al-Khwārizmī's Algebra

Despite their name, Arabic numerals have roots in India. The reason for this misnomer is Europeans saw the numerals used in an Arabic book, Concerning the Hindu Art of Reckoning, by Mohommed ibn-Musa al-Khwarizmi. Al-Khwārizmī wrote several important books on the Hindu–Arabic numerals and on methods for solving equations. His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi,[note 13] were instrumental in spreading Indian mathematics and Indian numerals to the West. Al-Khwarizmi did not claim the numerals as Arabic, but over several Latin translations, the fact that the numerals were Indian in origin was lost. The word algorithm is derived from the Latinization of Al-Khwārizmī's name, Algoritmi, and the word algebra from the title of one of his works, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completion and Balancing).

Islamic mathematics developed and expanded the mathematics known to Central Asian civilizations.[41] Al-Khwārizmī gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots,[42] and Al-Khwārizmī was to teach algebra in an elementary form and for its own sake.[43] Al-Khwārizmī also discussed the fundamental method of "reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as al-jabr.[44] His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." Al-Khwārizmī also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."[45]

Al-Karaji, in his treatise al-Fakhri, extends the methodology to incorporate integer powers and integer roots of unknown quantities.[note 14][46] The historian of mathematics, F. Woepcke,[47] praised Al-Karaji for being "the first who introduced the theory of algebraic calculus." Also in the 10th century, Abul Wafa translated the works of Diophantus into Arabic. Ibn al-Haytham would develop analytic geometry. Al-Haytham derived the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers. Al-Haytham performed an integration in order to find the volume of a paraboloid, and was able to generalize his result for the integrals of polynomials up to the fourth degree.[note 15][48] In the late 11th century, Omar Khayyam would develop algebraic geometry, wrote Discussions of the Difficulties in Euclid,[note 16] and wrote on the general geometric solution to cubic equations. Nasir al-Din Tusi (Nasireddin) made advances in spherical trigonometry. Muslim mathematicians during this period include the addition of the decimal point notation to the Arabic numerals.

The modern Arabic numeral symbols used around the world first appeared in Islamic North Africa in the 10th century. A distinctive Western Arabic variant of the Eastern Arabic numerals began to emerge around the 10th century in the Maghreb and Al-Andalus (sometimes called ghubar numerals, though the term is not always accepted), which are the direct ancestor of the modern Arabic numerals used throughout the world.[49]

Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe. In the 12th century, scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī's[note 17] and the complete text of Euclid's Elements.[note 18][50][51] One of the European books that advocated using the numerals was Liber Abaci, by Leonardo of Pisa, better known as Fibonacci. Liber Abaci is better known for the mathematical problem Fibonacci wrote in it about a population of rabbits. The growth of the population ended up being a Fibonacci sequence, where a term is the sum of the two preceding terms.

Symbolic stage

Symbols by popular introduction date

Early arithmetic and multiplication

The transition to symbolic algebra, where only symbols are used, can first be seen in the work of Ibn al-Banna' al-Marrakushi (1256–1321) and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1482).[52][53] Al-Qalasādī was the last major medieval Arab algebraist, who improved on the algebraic notation earlier used in the Maghreb by Ibn al-Banna.[54] In contrast to the syncopated notations of their predecessors, Diophantus and Brahmagupta, which lacked symbols for mathematical operations,[55] al-Qalasadi's algebraic notation was the first to have symbols for these functions and was thus "the first steps toward the introduction of algebraic symbolism." He represented mathematical symbols using characters from the Arabic alphabet.[54]

The 1489 use of the plus and minus signs in print.

The 14th century saw the development of new mathematical concepts to investigate a wide range of problems.[56] The two widely used arithmetic symbols are addition and subtraction, + and −. The plus sign was used by 1360 by Nicole Oresme[57][note 19] in his work Algorismus proportionum.[58] It is thought an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand sign also began as "et". Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled.[59] The minus sign was used in 1489 by Johannes Widmann in Mercantile Arithmetic or Behende und hüpsche Rechenung auff allen Kauffmanschafft,.[60] Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively.[61] In Summa de arithmetica, geometria, proportioni e proportionalità,[note 20][62] Luca Pacioli used symbols for plus and minus symbols and contained algebra.[note 21]

In the 15th century, Ghiyath al-Kashi computed the value of π to the 16th decimal place. Kashi also had an algorithm for calculating nth roots.[note 22] In 1533, Regiomontanus's table of sines and cosines were published.[63] Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equations. Gerolamo Cardano published them in his 1545 book Ars Magna, together with a solution for the quartic equations, discovered by his student Lodovico Ferrari. The radical symbol[note 23] for square root was introduced by Christoph Rudolff.[note 24] Michael Stifel's important work Arithmetica integra[64] contained important innovations in mathematical notation. In 1556, Niccolò Tartaglia used parentheses for precedence grouping. In 1557 Robert Recorde published The Whetstone of Witte which introduced the equal sign (=), as well as plus and minus signs for the English reader. In 1564, Gerolamo Cardano analyzed games of chance beginning the early stages of probability theory. In 1572 Rafael Bombelli published his L'Algebra in which he showed how to deal with the imaginary quantities that could appear in Cardano's formula for solving cubic equations. Simon Stevin's book De Thiende ('the art of tenths'), published in Dutch in 1585, contained a systematic treatment of decimal notation, which influenced all later work on the real number system. The New algebra (1591) of François Viète introduced the modern notational manipulation of algebraic expressions. For navigation and accurate maps of large areas, trigonometry grew to be a major branch of mathematics. Bartholomaeus Pitiscus coin the word "trigonometry", publishing his Trigonometria in 1595.

John Napier is best known as the inventor of logarithms[note 25][65] and made common the use of the decimal point in arithmetic and mathematics.[66][67] After Napier, Edmund Gunter created the logarithmic scales (lines, or rules) upon which slide rules are based, it was William Oughtred who used two such scales sliding by one another to perform direct multiplication and division; and he is credited as the inventor of the slide rule in 1622. In 1631 Oughtred introduced the multiplication sign (×) his proportionality sign,[note 26] and abbreviations sin and cos for the sine and cosine functions.[68] Albert Girard also used the abbreviations 'sin', 'cos' and 'tan' for the trigonometric functions in his treatise.

Johannes Kepler was one of the pioneers of the mathematical applications of infinitesimals.[note 27] René Descartes is credited as the father of analytical geometry, the bridge between algebra and geometry,[note 28] crucial to the discovery of infinitesimal calculus and analysis. In the 17th century, Descartes introduced Cartesian co-ordinates which allowed the development of analytic geometry.[note 29] Blaise Pascal influenced mathematics throughout his life. His Traité du triangle arithmétique ("Treatise on the Arithmetical Triangle") of 1653 described a convenient tabular presentation for binomial coefficients.[note 30] Pierre de Fermat and Blaise Pascal would investigate probability.[note 31] John Wallis introduced the infinity symbol.[note 32] He similarly used this notation for infinitesimals.[note 33] In 1657, Christiaan Huygens published the treatise on probability, On Reasoning in Games of Chance.[note 34][69]

Johann Rahn introduced the division sign (÷, an obelus variant repurposed) and the therefore sign in 1659. William Jones used π in Synopsis palmariorum mathesios[70] in 1706 because it is the initial letter of the Greek word perimetron (περιμετρον), which means perimeter in Greek. This usage was popularized in 1737 by Euler. In 1734, Pierre Bouguer used double horizontal bar below the inequality sign.[71]

Derivatives notation: Leibniz and Newton

Derivative notations
Sir Isaac Newton Gottfried Wilhelm Leibniz

The study of linear algebra emerged from the study of determinants, which were used to solve systems of linear equations. Calculus had two main systems of notation, each created by one of the creators: that developed by Isaac Newton and the notation developed by Gottfried Leibniz. Leibniz's is the notation used most often today. Newton's was simply a dot or dash placed above the function.[note 35] In modern usage, this notation generally denotes derivatives of physical quantities with respect to time, and is used frequently in the science of mechanics. Leibniz, on the other hand, used the letter d as a prefix to indicate differentiation, and introduced the notation representing derivatives as if they were a special type of fraction.[note 36] This notation makes explicit the variable with respect to which the derivative of the function is taken. Leibniz also created the integral symbol.[note 37] The symbol is an elongated S, representing the Latin word Summa, meaning "sum". When finding areas under curves, integration is often illustrated by dividing the area into infinitely many tall, thin rectangles, whose areas are added. Thus, the integral symbol is an elongated s, for sum.

High division operators and functions

Letters of the alphabet in this time were to be used as symbols of quantity; and although much diversity existed with respect to the choice of letters, there were to be several universally recognized rules in the following history.[24] Here thus in the history of equations the first letters of the alphabet were indicatively known as coefficients, the last letters the unknown terms (an incerti ordinis). In algebraic geometry, again, a similar rule was to be observed, the last letters of the alphabet there denoting the variable or current coordinates. Certain letters, such as ${\displaystyle \pi }$, ${\displaystyle e}$, etc., were by universal consent appropriated as symbols of the frequently occurring numbers 3.14159 ..., and 2.7182818 ....,[note 38] etc., and their use in any other acceptation was to be avoided as much as possible.[24] Letters, too, were to be employed as symbols of operation, and with them other previously mentioned arbitrary operation characters. The letters ${\displaystyle d}$, elongated ${\displaystyle S}$ were to be appropriated as operative symbols in the differential calculus and integral calculus, ${\displaystyle \Delta }$ and ∑ in the calculus of differences.[24] In functional notation, a letter, as a symbol of operation, is combined with another which is regarded as a symbol of quantity.[24][note 39]

Beginning in 1718, Thomas Twinin used the division slash (solidus), deriving it from the earlier Arabic horizontal fraction bar. Pierre-Simon, marquis de Laplace developed the widely used Laplacian differential operator.[note 40] In 1750, Gabriel Cramer developed "Cramer's Rule" for solving linear systems.

Euler and prime notations

Leonhard Euler's signature

Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. His contributions include his use of e to represent the base of natural logarithms. It is not known exactly why ${\displaystyle e}$ was chosen, but it was probably because the four letters of the alphabet were already commonly used to represent variables and other constants. Euler used ${\displaystyle \pi }$ to represent pi consistently. The use of ${\displaystyle \pi }$ was suggested by William Jones, who used it as shorthand for perimeter. Euler used ${\displaystyle i}$ to represent the square root of negative one,[note 41] although he earlier used it as an infinite number. [note 42][note 43] For summation, Euler used sigma, Σ.[note 44] For functions, Euler used the notation ${\displaystyle f(x)}$ to represent a function of ${\displaystyle x}$. In 1730, Euler wrote the gamma function.[note 45] In 1736, Euler produces his paper on the Seven Bridges of Königsberg[72] initiating the study of graph theory.

The mathematician William Emerson[73] would develop the proportionality sign.[note 46][note 47][74][75] Much later in the abstract expressions of the value of various proportional phenomena, the parts-per notation would become useful as a set of pseudo units to describe small values of miscellaneous dimensionless quantities. Marquis de Condorcet, in 1768, advanced the partial differential sign.[note 48] In 1771, Alexandre-Théophile Vandermonde deduced the importance of topological features when discussing the properties of knots related to the geometry of position. Between 1772 and 1788, Joseph-Louis Lagrange re-formulated the formulas and calculations of Classical "Newtonian" mechanics, called Lagrangian mechanics. The prime symbol for derivatives was also made by Lagrange.

But in our opinion truths of this kind should be drawn from notions rather than from notations.

— Carl Friedrich Gauss[note 49]

Gauss, Hamilton, and Matrix notations

At the turn of the 19th century, Carl Friedrich Gauss developed the identity sign for congruence relation and, in Quadratic reciprocity, the integral part. Gauss contributed functions of complex variables, in geometry, and on the convergence of series. He gave the satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law. Gauss developed the theory of solving linear systems by using Gaussian elimination, which was initially listed as an advancement in geodesy.[76] He would also develop the product sign. Also in this time, Niels Henrik Abel and Évariste Galois[note 50] conducted their work on the solvability of equations, linking group theory and field theory.

After the 1800s, Christian Kramp would promote factorial notation during his research in generalized factorial function which applied to non-integers.[77] Joseph Diaz Gergonne introduced the set inclusion signs.[note 51] Peter Gustav Lejeune Dirichlet developed Dirichlet L-functions to give the proof of Dirichlet's theorem on arithmetic progressions and began analytic number theory.[note 52] In 1828, Gauss proved his Theorema Egregium (remarkable theorem in Latin), establishing property of surfaces. In the 1830s, George Green developed Green's function. In 1829. Carl Gustav Jacob Jacobi publishes Fundamenta nova theoriae functionum ellipticarum with his elliptic theta functions. By 1841, Karl Weierstrass, the "father of modern analysis", elaborated on the concept of absolute value and the determinant of a matrix.

Matrix notation would be more fully developed by Arthur Cayley in his three papers, on subjects which had been suggested by reading the Mécanique analytique[78] of Lagrange and some of the works of Laplace. Cayley defined matrix multiplication and matrix inverses. Cayley used a single letter to denote a matrix,[79] thus treating a matrix as an aggregate object. He also realized the connection between matrices and determinants,[80] and wrote "There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants".[81]

[... The mathematical quaternion] has, or at least involves a reference to, four dimensions.

— William Rowan Hamilton[note 53]

William Rowan Hamilton would introduce the nabla symbol[note 54] for vector differentials.[82][83] This was previously used by Hamilton as a general-purpose operator sign.[84] Hamilton reformulated Newtonian mechanics, now called Hamiltonian mechanics. This work has proven central to the modern study of classical field theories such as electromagnetism. This was also important to the development of quantum mechanics.[note 55] In mathematics, he is perhaps best known as the inventor of quaternion notation[note 56] and biquaternions. Hamilton also introduced the word "tensor" in 1846.[85][note 57] James Cockle would develop the tessarines[note 58] and, in 1849, coquaternions. In 1848, James Joseph Sylvester introduced into matrix algebra the term matrix.[note 59]

Maxwell, Clifford, and Ricci notations

James Clerk Maxwell

---

Maxwell's most prominent achievement was to formulate a set of equations that united previously unrelated observations, experiments, and equations of electricity, magnetism, and optics into a consistent theory.[86]

In 1864 James Clerk Maxwell reduced all of the then current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in A Dynamical Theory of the Electromagnetic Field.[87] (See Maxwell's equations.) The method of calculation which it is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used they are known as Lagrange's equations. In 1871 Richard Dedekind called a set of real or complex numbers which is closed under the four arithmetic operations a field. In 1873 Maxwell presented A Treatise on Electricity and Magnetism.

In 1878, William Kingdon Clifford published his Elements of Dynamic.[88] Clifford developed split-biquaternions,[note 60] which he called algebraic motors. Clifford obviated quaternion study by separating the dot product and cross product of two vectors from the complete quaternion notation.[note 61] This approach made vector calculus available to engineers and others working in three dimensions and skeptical of the lead–lag effect[note 62] in the fourth dimension.[note 63] The common vector notations are used when working with vectors which are spatial or more abstract members of vector spaces, while angle notation (or phasor notation) is a notation used in electronics.

In 1881, Leopold Kronecker defined what he called a "domain of rationality", which is a field extension of the field of rational numbers in modern terms.[89] In 1882, Hüseyin Tevfik Paşa wrote the book titled "Linear Algebra".[90][91] Lord Kelvin's aetheric atom theory (1860s) led Peter Guthrie Tait, in 1885, to publish a topological table of knots with up to ten crossings known as the Tait conjectures. In 1893, Heinrich M. Weber gave the clear definition of an abstract field.[note 64] Tensor calculus was developed by Gregorio Ricci-Curbastro between 1887–96, presented in 1892 under the title absolute differential calculus,[92] and the contemporary usage of "tensor" was stated by Woldemar Voigt in 1898.[93] In 1895, Henri Poincaré published Analysis Situs.[94] In 1897, Charles Proteus Steinmetz would publish Theory and Calculation of Alternating Current Phenomena, with the assistance of Ernst J. Berg.[95]

From formula mathematics to tensors

The above proposition is occasionally useful.

— Bertrand Russell [note 65]

In 1895 Giuseppe Peano issued his Formulario mathematico,[96] an effort to digest mathematics into terse text based on special symbols. He would provide a definition of a vector space and linear map. He would also introduce the intersection sign, the union sign, the membership sign (is an element of), and existential quantifier[note 66] (there exists). Peano would pass to Bertrand Russell his work in 1900 at a Paris conference; it so impressed Russell that Russell too was taken with the drive to render mathematics more concisely. The result was Principia Mathematica written with Alfred North Whitehead. This treatise marks a watershed in modern literature where symbol became dominant.[note 67] Ricci-Curbastro and Tullio Levi-Civita popularized the tensor index notation around 1900.[97]

Mathematical logic and abstraction

Abstraction
Felix Klein Georg Cantor

At the beginning of this period, Felix Klein's "Erlangen program" identified the underlying theme of various geometries, defining each of them as the study of properties invariant under a given group of symmetries. This level of abstraction revealed connections between geometry and abstract algebra. Georg Cantor[note 68] would introduce the aleph symbol for cardinal numbers of transfinite sets.[note 69] His notation for the cardinal numbers was the Hebrew letter ${\displaystyle \aleph }$ (aleph) with a natural number subscript; for the ordinals he employed the Greek letter ω (omega). This notation is still in use today in ordinal notation of a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language. His theory created a great deal of controversy. Cantor would, in his study of Fourier series, consider point sets in Euclidean space.

After the turn of the 20th century, Josiah Willard Gibbs would in physical chemistry introduce middle dot for dot product and the multiplication sign for cross products. He would also supply notation for the scalar and vector products, which was introduced in Vector Analysis. In 1904, Ernst Zermelo promotes axiom of choice and his proof of the well-ordering theorem.[98] Bertrand Russell would shortly afterward introduce logical disjunction (OR) in 1906. Also in 1906, Poincaré would publish On the Dynamics of the Electron[99] and Maurice Fréchet introduced metric space.[100] Later, Gerhard Kowalewski and Cuthbert Edmund Cullis[101][102][103] would successively introduce matrices notation, parenthetical matrix and box matrix notation respectively. After 1907, mathematicians[note 70] studied knots from the point of view of the knot group and invariants from homology theory.[note 71] In 1908, Joseph Wedderburn's structure theorems were formulated for finite-dimensional algebras over a field. Also in 1908, Ernst Zermelo proposed "definite" property and the first axiomatic set theory, Zermelo set theory. In 1910 Ernst Steinitz published the influential paper Algebraic Theory of Fields.[note 72][note 73] In 1911, Steinmetz would publish Theory and Calculation of Transient Electric Phenomena and Oscillations.

Albert Einstein in 1921

Albert Einstein, in 1916, introduced the Einstein notation[note 74] which summed over a set of indexed terms in a formula, thus exerting notational brevity. Arnold Sommerfeld would create the contour integral sign in 1917. Also in 1917, Dimitry Mirimanoff proposes axiom of regularity. In 1919, Theodor Kaluza would solve general relativity equations using five dimensions, the results would have electromagnetic equations emerge.[104] This would be published in 1921 in "Zum Unitätsproblem der Physik".[105] In 1922, Abraham Fraenkel and Thoralf Skolem independently proposed replacing the axiom schema of specification with the axiom schema of replacement. Also in 1922, Zermelo–Fraenkel set theory was developed. In 1923, Steinmetz would publish Four Lectures on Relativity and Space. Around 1924, Jan Arnoldus Schouten would develop the modern notation and formalism for the Ricci calculus framework during the absolute differential calculus applications to general relativity and differential geometry in the early twentieth century.[note 75][106][107][108] In 1925, Enrico Fermi would describe a system comprising many identical particles that obey the Pauli exclusion principle, afterwards developing a diffusion equation (Fermi age equation). In 1926, Oskar Klein would develop the Kaluza–Klein theory. In 1928, Emil Artin abstracted ring theory with Artinian rings. In 1933, Andrey Kolmogorov introduces the Kolmogorov axioms. In 1937, Bruno de Finetti deduced the "operational subjective" concept.

Mathematical symbolism

Mathematical abstraction began as a process of extracting the underlying essence of a mathematical concept,[109][110] removing any dependence on real world objects with which it might originally have been connected,[111] and generalizing it so that it has wider applications or matching among other abstract descriptions of equivalent phenomena. Two abstract areas of modern mathematics are category theory and model theory. Bertrand Russell,[112] said, "Ordinary language is totally unsuited for expressing what physics really asserts, since the words of everyday life are not sufficiently abstract. Only mathematics and mathematical logic can say as little as the physicist means to say". Though, one can substituted mathematics for real world objects, and wander off through equation after equation, and can build a concept structure which has no relation to reality.[113]

Symbolic logic studies the purely formal properties of strings of symbols. The interest in this area springs from two sources. First, the notation used in symbolic logic can be seen as representing the words used in philosophical logic. Second, the rules for manipulating symbols found in symbolic logic can be implemented on a computing machine. Symbolic logic is usually divided into two subfields, propositional logic and predicate logic. Other logics of interest include temporal logic, modal logic and fuzzy logic. The area of symbolic logic called propositional logic, also called propositional calculus, studies the properties of sentences formed from constants[note 76] and logical operators. The corresponding logical operations are known, respectively, as conjunction, disjunction, material conditional, biconditional, and negation. These operators are denoted as keywords[note 77] and by symbolic notation.

Some of the introduced mathematical logic notation during this time included the set of symbols used in Boolean algebra. This was created by George Boole in 1854. Boole himself did not see logic as a branch of mathematics, but it has come to be encompassed anyway. Symbols found in Boolean algebra include ${\displaystyle \land }$ (AND), ${\displaystyle \lor }$ (OR), and ${\displaystyle \lnot }$ (not). With these symbols, and letters to represent different truth values, one can make logical statements such as ${\displaystyle a\lor \lnot a=1}$, that is "(a is true OR a is not true) is true", meaning it is true that a is either true or not true (i.e. false). Boolean algebra has many practical uses as it is, but it also was the start of what would be a large set of symbols to be used in logic.[note 78] Predicate logic, originally called predicate calculus, expands on propositional logic by the introduction of variables[note 79] and by sentences containing variables, called predicates.[note 80] In addition, predicate logic allows quantifiers.[note 81] With these logic symbols and additional quantifiers from predicate logic,[note 82] valid proofs can be made that are irrationally artificial,[note 83] but syntactical.[note 84]

Gödel incompleteness notation

To every ω-consistent recursive class κ of formulae there correspond recursive class signs r, such that neither v Gen r nor Neg (v Gen r) belongs to Flg (κ) (where v is the free variable of r).

— Kurt Gödel[114]

While proving his incompleteness theorems,[note 85] Kurt Gödel created an alternative to the symbols normally used in logic. He used Gödel numbers, which were numbers that represented operations with set numbers, and variables with the prime numbers greater than 10. With Gödel numbers, logic statements can be broken down into a number sequence. Gödel then took this one step farther, taking the n prime numbers and putting them to the power of the numbers in the sequence. These numbers were then multiplied together to get the final product, giving every logic statement its own number.[115][note 86]

Contemporary notation and topics

Early 20th-century notation

Abstraction of notation is an ongoing process and the historical development of many mathematical topics exhibits a progression from the concrete to the abstract. Various set notations would be developed for fundamental object sets. Around 1924, David Hilbert and Richard Courant published "Methods of mathematical physics. Partial differential equations".[116] In 1926, Oskar Klein and Walter Gordon proposed the Klein–Gordon equation to describe relativistic particles.[note 87] The first formulation of a quantum theory describing radiation and matter interaction is due to Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom.[117] In 1928, the relativistic Dirac equation was formulated by Dirac to explain the behavior of the relativistically moving electron.[note 88] Dirac described the quantification of the electromagnetic field as an ensemble of harmonic oscillators with the introduction of the concept of creation and annihilation operators of particles. In the following years, with contributions from Wolfgang Pauli, Eugene Wigner, Pascual Jordan, and Werner Heisenberg, and an elegant formulation of quantum electrodynamics due to Enrico Fermi,[118] physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles.

In 1931, Alexandru Proca developed the Proca equation (Euler–Lagrange equation)[note 89] for the vector meson theory of nuclear forces and the relativistic quantum field equations. John Archibald Wheeler in 1937 develops S-matrix. Studies by Felix Bloch with Arnold Nordsieck,[119] and Victor Weisskopf,[120] in 1937 and 1939, revealed that such computations were reliable only at a first order of perturbation theory, a problem already pointed out by Robert Oppenheimer.[121] At higher orders in the series infinities emerged, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity and quantum mechanics.

In the 1930s, the double-struck capital Z for integer number sets was created by Edmund Landau. Nicolas Bourbaki created the double-struck capital Q for rational number sets. In 1935, Gerhard Gentzen made universal quantifiers. In 1936, Tarski's undefinability theorem is stated by Alfred Tarski and proved.[note 90] In 1938, Gödel proposes the constructible universe in the paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". André Weil and Nicolas Bourbaki would develop the empty set sign in 1939. That same year, Nathan Jacobson would coin the double-struck capital C for complex number sets.

Around the 1930s, Voigt notation[note 91] would be developed for multilinear algebra as a way to represent a symmetric tensor by reducing its order. Schönflies notation[note 92] became one of two conventions used to describe point groups (the other being Hermann–Mauguin notation). Also in this time, van der Waerden notation[122][123] became popular for the usage of two-component spinors (Weyl spinors) in four spacetime dimensions. Arend Heyting would introduce Heyting algebra and Heyting arithmetic.

The arrow, e.g., →, was developed for function notation in 1936 by Øystein Ore to denote images of specific elements.[note 93][note 94] Later, in 1940, it took its present form, e.g., f: X → Y, through the work of Witold Hurewicz. Werner Heisenberg, in 1941, proposed the S-matrix theory of particle interactions.

Paul Dirac, pictured here, made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics.

Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals. It is so called because the inner product (or dot product on a complex vector space) of two states is denoted by a ⟨bra|ket⟩[note 95] consisting of a left part, ⟨φ|, and a right part, |ψ⟩. The notation was introduced in 1939 by Paul Dirac,[124] though the notation has precursors in Grassmann's use of the notation [φ|ψ] for his inner products nearly 100 years previously.[125]

Bra–ket notation is widespread in quantum mechanics: almost every phenomenon that is explained using quantum mechanics—including a large portion of modern physics—is usually explained with the help of bra–ket notation. The notation establishes an encoded abstract representation-independence, producing a versatile specific representation (e.g., x, or p, or eigenfunction base) without much ado, or excessive reliance on, the nature of the linear spaces involved. The overlap expression ⟨φ|ψ⟩ is typically interpreted as the probability amplitude for the state ψ to collapse into the state ϕ. The Feynman slash notation (Dirac slash notation[126]) was developed by Richard Feynman for the study of Dirac fields in quantum field theory.

In 1948, Valentine Bargmann and Eugene Wigner proposed the relativistic Bargmann–Wigner equations to describe free particles and the equations are in the form of multi-component spinor field wavefunctions. In 1950, William Vallance Douglas Hodge presented "The topological invariants of algebraic varieties" at the Proceedings of the International Congress of Mathematicians. Between 1954 and 1957, Eugenio Calabi worked on the Calabi conjecture for Kähler metrics and the development of Calabi–Yau manifolds. In 1957, Tullio Regge formulated the mathematical property of potential scattering in the Schrödinger equation.[note 96] Stanley Mandelstam, along with Regge, did the initial development of the Regge theory of strong interaction phenomenology. In 1958, Murray Gell-Mann and Richard Feynman, along with George Sudarshan and Robert Marshak, deduced the chiral structures of the weak interaction in physics. Geoffrey Chew, along with others, would promote matrix notation for the strong interaction, and the associated bootstrap principle, in 1960. In the 1960s, set-builder notation was developed for describing a set by stating the properties that its members must satisfy. Also in the 1960s, tensors are abstracted within category theory by means of the concept of monoidal category. Later, multi-index notation eliminates conventional notions used in multivariable calculus, partial differential equations, and the theory of distributions, by abstracting the concept of an integer index to an ordered tuple of indices.

Modern mathematical notation

In the modern mathematics of special relativity, electromagnetism and wave theory, the d'Alembert operator[note 97][note 98] is the Laplace operator of Minkowski space. The Levi-Civita symbol[note 99] is used in tensor calculus.

After the full Lorentz covariance formulations that were finite at any order in a perturbation series of quantum electrodynamics, Sin-Itiro Tomonaga, Julian Schwinger and Richard Feynman were jointly awarded with a Nobel prize in physics in 1965.[127] Their contributions, and those of Freeman Dyson, were about covariant and gauge invariant formulations of quantum electrodynamics that allow computations of observables at any order of perturbation theory. Feynman's mathematical technique, based on his diagrams, initially seemed very different from the field-theoretic, operator-based approach of Schwinger and Tomonaga, but Freeman Dyson later showed that the two approaches were equivalent. Renormalization, the need to attach a physical meaning at certain divergences appearing in the theory through integrals, has subsequently become one of the fundamental aspects of quantum field theory and has come to be seen as a criterion for a theory's general acceptability. Quantum electrodynamics has served as the model and template for subsequent quantum field theories. Peter Higgs, Jeffrey Goldstone, and others, Sheldon Glashow, Steven Weinberg and Abdus Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force. In the late 1960s, the particle zoo was composed of the then known elementary particles before the discovery of quarks.

Standard model of elementary particles.

---

The fundamental fermions and the fundamental bosons. (c.2008)[note 100] Based on the proprietary publication, Review of Particle Physics.[note 101]

A step towards the Standard Model was Sheldon Glashow's discovery, in 1960, of a way to combine the electromagnetic and weak interactions.[128] In 1967, Steven Weinberg[129] and Abdus Salam[130] incorporated the Higgs mechanism[131][132][133] into Glashow's electroweak theory, giving it its modern form. The Higgs mechanism is believed to give rise to the masses of all the elementary particles in the Standard Model. This includes the masses of the W and Z bosons, and the masses of the fermions – i.e. the quarks and leptons. Also in 1967, Bryce DeWitt published his equation under the name "Einstein–Schrödinger equation" (later renamed the "Wheeler–DeWitt equation").[134] In 1969, Yoichiro Nambu, Holger Bech Nielsen, and Leonard Susskind described space and time in terms of strings. In 1970, Pierre Ramond develop two-dimensional supersymmetries. Michio Kaku and Keiji Kikkawa would afterwards formulate string variations. In 1972, Michael Artin, Alexandre Grothendieck, Jean-Louis Verdier propose the Grothendieck universe.[135]

After the neutral weak currents caused by
Z
boson exchange were discovered at CERN in 1973,[136][137][138][139] the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 Nobel Prize in Physics for discovering it. The theory of the strong interaction, to which many contributed, acquired its modern form around 1973–74. With the establishment of quantum chromodynamics, a finalized a set of fundamental and exchange particles, which allowed for the establishment of a "standard model" based on the mathematics of gauge invariance, which successfully described all forces except for gravity, and which remains generally accepted within the domain to which it is designed to be applied. In the late 1970s, William Thurston introduced hyperbolic geometry into the study of knots with the hyperbolization theorem. The orbifold notation system, invented by Thurston, has been developed for representing types of symmetry groups in two-dimensional spaces of constant curvature. In 1978, Shing-Tung Yau deduced that the Calabi conjecture have Ricci flat metrics. In 1979, Daniel Friedan showed that the equations of motions of string theory are abstractions of Einstein equations of General Relativity.

The first superstring revolution is composed of mathematical equations developed between 1984 and 1986. In 1984, Vaughan Jones deduced the Jones polynomial and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. According to string theory, all particles in the "particle zoo" have a common ancestor, namely a vibrating string. In 1985, Philip Candelas, Gary Horowitz,[140] Andrew Strominger, and Edward Witten would publish "Vacuum configurations for superstrings"[141] Later, the tetrad formalism (tetrad index notation) would be introduced as an approach to general relativity that replaces the choice of a coordinate basis by the less restrictive choice of a local basis for the tangent bundle.[note 102][142]

In the 1990s, Roger Penrose would propose Penrose graphical notation (tensor diagram notation) as a, usually handwritten, visual depiction of multilinear functions or tensors.[143] Penrose would also introduce abstract index notation.[note 103] In 1995, Edward Witten suggested M-theory and subsequently used it to explain some observed dualities, initiating the second superstring revolution.[note 104]

John H Conway, prolific mathematician of notation.

John Conway would further various notations, including the Conway chained arrow notation, the Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter and Norman Johnson more comprehensively defined it.

Combinatorial LCF notation[note 105] has been developed for the representation of cubic graphs that are Hamiltonian.[144][145] The cycle notation is the convention for writing down a permutation in terms of its constituent cycles.[146] This is also called circular notation and the permutation called a cyclic or circular permutation.[147]

Computers and markup notation

In 1931, IBM produces the IBM 601 Multiplying Punch; it is an electromechanical machine that could read two numbers, up to 8 digits long, from a card and punch their product onto the same card.[148] In 1934, Wallace Eckert used a rigged IBM 601 Multiplying Punch to automate the integration of differential equations.[149] In 1936, Alan Turing publishes "On Computable Numbers, With an Application to the Entscheidungsproblem".[150][note 106] John von Neumann, pioneer of the digital computer and of computer science,[note 107] in 1945, writes the incomplete First Draft of a Report on the EDVAC. In 1962, Kenneth E. Iverson developed an integral part notation, which became APL, for manipulating arrays that he taught to his students, and described in his book A Programming Language. In 1970, Edgar F. Codd proposed relational algebra as a relational model of data for database query languages. In 1971, Stephen Cook publishes "The complexity of theorem proving procedures"[151] In the 1970s within computer architecture, Quote notation was developed for a representing number system of rational numbers. Also in this decade, the Z notation (just like the APL language, long before it) uses many non-ASCII symbols, the specification includes suggestions for rendering the Z notation symbols in ASCII and in LaTeX. There are presently various C mathematical functions (Math.h) and numerical libraries. They are libraries used in software development for performing numerical calculations. These calculations can be handled by symbolic executions; analyzing a program to determine what inputs cause each part of a program to execute. Mathematica and SymPy are examples of computational software programs based on symbolic mathematics.

Future of mathematical notation

A section of a quintic Calabi–Yau three-fold (3D projection); recalling atomic vortex theory.

In the history of mathematical notation, ideographic symbol notation has come full circle with the rise of computer visualization systems. The notations can be applied to abstract visualizations, such as for rendering some projections of a Calabi-Yau manifold. Examples of abstract visualization which properly belong to the mathematical imagination can be found in computer graphics. The need for such models abounds, for example, when the measures for the subject of study are actually random variables and not really ordinary mathematical functions.

See also

Main relevance

Abuse of notation, Well-formed formula, Big O notation (L-notation), Dowker notation, Hungarian notation, Infix notation, Positional notation, Polish notation (Reverse Polish notation), Sign-value notation, History of writing numbers

Numbers and quantities

List of numbers, Irrational and suspected irrational numbers, γ, ζ(3), √2, √3, √5, φ, ρ, δ_S, α, e, π, δ, Physical constants, c, ε₀, h, G, Greek letters used in mathematics, science, and engineering

General relevance

Order of operations, Scientific notation (Engineering notation), Actuarial notation

Dot notation

Chemical notation (Lewis dot notation (Electron dot notation)), Dot-decimal notation

Arrow notation

Knuth's up-arrow notation, infinitary combinatorics (Arrow notation (Ramsey theory))

Geometries

Projective geometry, Affine geometry, Finite geometry

Lists and outlines

Outline of mathematics (Mathematics history topics and Mathematics topics (Mathematics categories)), Mathematical theories ( First-order theories, Theorems and Disproved mathematical ideas), Mathematical proofs (Incomplete proofs), Mathematical identities, Mathematical series, Mathematics reference tables, Mathematical logic topics, Mathematics-based methods, Mathematical functions, Transforms and Operators, Points in mathematics, Mathematical shapes, Knots (Prime knots and Mathematical knots and links), Inequalities, Mathematical concepts named after places, Mathematical topics in classical mechanics, Mathematical topics in quantum theory, Mathematical topics in relativity, String theory topics, Unsolved problems in mathematics, Mathematical jargon, Mathematical examples, Mathematical abbreviations, List of mathematical symbols

Misc.

Hilbert's problems, Mathematical coincidence, Chess notation, Line notation, Musical notation (Dotted note), Whyte notation, Dice notation, recursive categorical syntax

People

Mathematicians (Amateur mathematicians and Female mathematicians), Thomas Bradwardine, Thomas Harriot, Felix Hausdorff, Gaston Julia, Helge von Koch, Paul Lévy, Aleksandr Lyapunov, Benoit Mandelbrot, Lewis Fry Richardson, Wacław Sierpiński, Saunders Mac Lane, Paul Cohen, Gottlob Frege, G. S. Carr, Robert Recorde, Bartel Leendert van der Waerden, G. H. Hardy, E. M. Wright, James R. Newman, Carl Gustav Jacob Jacobi, Roger Joseph Boscovich, Eric W. Weisstein, Mathematical probabilists, Statisticians

Notes

1. Or the Middle Ages.
2. Such characters, in fact, are preserved with little alteration in the Roman notation, an account of which may be found in John Leslie's Philosophy of Arithmetic.
3. Number theory is branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers).
4. Greek: μή μου τοὺς κύκλους τάραττε
5. That is, ${\displaystyle a^{2}+b^{2}=c^{2}}$.
6. Magnitude (mathematics), the relative size of an object ; Magnitude (vector), a term for the size or length of a vector; Scalar (mathematics), a quantity defined only by its magnitude; Euclidean vector, a quantity defined by both its magnitude and its direction; Order of magnitude, the class of scale having a fixed value ratio to the preceding class.
7. Autolycus' On the Moving Sphere is another ancient mathematical manuscript of the time.
8. Proclus, a Greek mathematician who lived several centuries after Euclid, wrote in his commentary of the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors".
9. The expression:
   ${\displaystyle 2x^{4}+3x^{3}-4x^{2}+5x-6}$
   would be written as:
   SS2 C3 x5 M S4 u6
   .
10. such as the rule, square, compasses, water level (reed level), and plumb-bob.
11. such as the wheel and axle
12. The area of the square described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the squares described on the sides
13. Al-Kindi also introduced cryptanalysis and frequency analysis.
14. Something close to a proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal's triangle, and the sum of integral cubes.
15. He thus came close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.
16. a book about what he perceived as flaws in Euclid's Elements, especially the parallel postulate
17. translated into Latin by Robert of Chester
18. translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona
19. His own personal use started around 1351.
20. Summa de Arithmetica: Geometria Proportioni et Proportionalita. Tr. Sum of Arithmetic: Geometry in proportions and proportionality.
21. Much of the work originated from Piero Della Francesca whom he appropriated and purloined.
22. This was a special case of the methods given many centuries later by Ruffini and Horner.
23. That is, ${\displaystyle {\sqrt {~}}}$.
24. Because, it is thought, it resembled a lowercase "r" (for "radix").
25. Published in Description of the Marvelous Canon of Logarithms
26. That is,
    ∷
27. see Law of Continuity.
28. Using Cartesian coordinates on the plane, the distance between two points (x₁, y₁) and (x₂, y₂) is defined by the formula:
    ${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},}$
    which can be viewed as a version of the Pythagorean theorem.
29. Further steps in abstraction were taken by Lobachevsky, Bolyai, Riemann, and Gauss who generalised the concepts of geometry to develop non-Euclidean geometries.
30. Now called Pascal's triangle.
31. For example, the "problem of points".
32. That is, ${\displaystyle {\infty }}$.
33. For example, ${\displaystyle {\frac {1}{\infty }}.}$
34. Original title, "De ratiociniis in ludo aleae"
35. For example, the derivative of the function x would be written as ${\displaystyle {\dot {x}}}$. The second derivative of x would be written as ${\displaystyle {\ddot {x}}}$, etc.
36. For example, the derivative of the function x with respect to the variable t in Leibniz's notation would be written as ${\displaystyle {dx \over dt}}$.
37. That is, ${\displaystyle \int _{-N}^{N}f(x)\,dx}$.
38. See also: List of representations of e
39. Thus ${\displaystyle f(x)}$ denotes the mathematical result of the performance of the operation ${\displaystyle f}$ upon the subject ${\displaystyle x}$. If upon this result the same operation were repeated, the new result would be expressed by ${\displaystyle f[f(x)]}$, or more concisely by ${\displaystyle f^{2}(x)}$, and so on. The quantity ${\displaystyle x}$ itself regarded as the result of the same operation ${\displaystyle f}$ upon some other function; the proper symbol for which is, by analogy, ${\displaystyle f^{-1}(x)}$. Thus ${\displaystyle f}$ and ${\displaystyle f^{-1}}$ are symbols of inverse operations, the former cancelling the effect of the latter on the subject ${\displaystyle x}$. ${\displaystyle f(x)}$ and ${\displaystyle f^{-1}(x)}$ in a similar manner are termed inverse functions.
40. That is, ${\displaystyle \Delta f(p)}$
41. That is, ${\displaystyle {\sqrt {-1}}}$
42. Today, the symbol created by John Wallis, ${\displaystyle \infty }$, is used for infinity.
43. As in, ${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}}$
44. Capital-sigma notation uses a symbol that compactly represents summation of many similar terms: the summation symbol, ∑, an enlarged form of the upright capital Greek letter Sigma. This is defined as:
    
    ${\displaystyle \sum _{i=m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}.}$
    
    Where, i represents the index of summation; a_i is an indexed variable representing each successive term in the series; m is the lower bound of summation, and n is the upper bound of summation. The "i = m" under the summation symbol means that the index i starts out equal to m. The index, i, is incremented by 1 for each successive term, stopping when i = n.
45. That is, ${\displaystyle n!=\int _{0}^{1}(-\ln s)^{n}\,{\rm {d}}s}$.
    valid for n > 0.
46. That is,
    ∝
47. Proportionality is the ratio of one quantity to another, especially the ratio of a part compared to a whole. In a mathematical context, a proportion is the statement of equality between two ratios; See Proportionality (mathematics), the relationship of two variables whose ratio is constant. See also aspect ratio, geometric proportions.
48. The curly d or Jacobi's delta.
49. About the proof of Wilson's theorem. Disquisitiones Arithmeticae (1801) Article 76
50. Galois theory and Galois geometry is named after him.
51. That is, "subset of" and "superset of"; This would later be redeveloped by Ernst Schröder.
52. A science of numbers that uses methods from mathematical analysis to solve problems about the integers.
53. Quoted in Robert Perceval Graves' Life of Sir William Rowan Hamilton (3 volumes, 1882, 1885, 1889)
54. That is, ${\displaystyle \nabla }$ (or, later called del, ∇)
55. See Hamiltonian (quantum mechanics).
56. That is, ${\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1}$
57. Though his use describes something different from what is now meant by a tensor. Namely, the norm operation in a certain type of algebraic system (now known as a Clifford algebra).
58. That is,
    ${\displaystyle t=w+xi+yj+zk,\quad w,x,y,z\in \mathbb {R} }$
    where
    ${\displaystyle ij=ji=k,\quad i^{2}=-1,\quad j^{2}=+1.}$
59. This is Latin for "womb".
60. That is, ${\displaystyle q=w+xi+yj+zk}$
61. Clifford intersected algebra with Hamilton's quaternions by replacing Hermann Grassmann's rule e_pe_p = 0 by the rule e_pe_p = 1. For more details, see exterior algebra.
62. See: Phasor, Group (mathematics), Signal velocity, Polyphase system, Harmonic oscillator, and RLC series circuit
63. Or the concept of a fourth spatial dimension. See also: Spacetime, the unification of time and space as a four-dimensional continuum; and, Minkowski space, the mathematical setting for special relativity.
64. See also: Mathematic fields and Field extension
65. Comment after the proof that 1+1=2, completed in Principia mathematica, by Alfred North Whitehead ... and Bertrand Russell. Volume II, 1st edition (1912)
66. This raises questions of the pure existence theorems.
67. Peano's Formulario Mathematico, though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4200 formulas and theorems.
68. Inventor of set theory
69. Transfinite arithmetic is the generalization of elementary arithmetic to infinite quantities like infinite sets; See Transfinite numbers, Transfinite induction, and Transfinite interpolation. See also Ordinal arithmetic.
70. Such as Max Dehn, J. W. Alexander, and others.
71. Such as the Alexander polynomial.
72. (German: Algebraische Theorie der Körper)
73. In this paper Steinitz axiomatically studied the properties of fields and defined many important field theoretic concepts like prime field, perfect field and the transcendence degree of a field extension.
74. The indices range over set {1, 2, 3},
    ${\displaystyle y=\sum _{i=1}^{3}c_{i}x^{i}=c_{1}x^{1}+c_{2}x^{2}+c_{3}x^{3}}$
    is reduced by the convention to:
    ${\displaystyle y=c_{i}x^{i}\,.}$
    Upper indices are not exponents but are indices of coordinates, coefficients or basis vectors.
    See also: Ricci calculus
75. Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. See also: Synge J.L.; Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6–108.
76. Here a logical constant is a symbol in symbolic logic that has the same meaning in all models, such as the symbol "=" for "equals".
    A constant, in a mathematical context, is a number that arises naturally in mathematics, such as π or e; Such mathematics constant value do not change. It can mean polynomial constant term (the term of degree 0) or the constant of integration, a free parameter arising in integration.
    Related, the physical constant are a physical quantity generally believed to be universal and unchanging. Programming constants are a values that, unlike a variable, cannot be reassociated with a different value.
77. Though not an index term, keywords are terms that represent information. A keyword is a word with special meaning (this is a semantic definition), while syntactically these are terminal symbols in the phrase grammar. See reserved word for the related concept.
78. Most of these symbols can be found in propositional calculus, a formal system described as ${\displaystyle {\mathcal {L}}={\mathcal {L}}\ (\mathrm {A} ,\ \Omega ,\ \mathrm {Z} ,\ \mathrm {I} )}$. ${\displaystyle \mathrm {A} }$ is the set of elements, such as the a in the example with Boolean algebra above. ${\displaystyle \Omega }$ is the set that contains the subsets that contain operations, such as ${\displaystyle \lor }$ or ${\displaystyle \land }$. ${\displaystyle \mathrm {Z} }$ contains the inference rules, which are the rules dictating how inferences may be logically made, and ${\displaystyle \mathrm {I} }$ contains the axioms. See also: Basic and Derived Argument Forms.
79. Usually denoted by x, y, z, or other lowercase letters
    Here a symbols that represents a quantity in a mathematical expression, a mathematical variable as used in many sciences.
    Variables can be symbolic name associated with a value and whose associated value may be changed, known in computer science as a variable reference. A variable can also be the operationalized way in which the attribute is represented for further data processing (e.g., a logical set of attributes). See also: Dependent and independent variables in statistics.
80. Usually denoted by an uppercase letter followed by a list of variables, such as P(x) or Q(y,z)
    Here a mathematical logic predicate, a fundamental concept in first-order logic. Grammatical predicates are grammatical components of a sentence.
    Related is the syntactic predicate in parser technology which are guidelines for the parser process. In computer programming, a branch predication allows a choice to execute or not to execute a given instruction based on the content of a machine register.
81. Representing ALL and EXISTS
82. e.g. ∃ for "there exists" and ∀ for "for all"
83. See also: Dialetheism, Contradiction, and Paradox
84. Related, facetious abstract nonsense describes certain kinds of arguments and methods related to category theory which resembles comical literary non sequitur devices (not illogical non sequiturs).
85. Gödel's incompleteness theorems shows that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a contested negative answer to Hilbert's second problem
86. For example, take the statement "There exists a number x such that it is not y". Using the symbols of propositional calculus, this would become: ${\displaystyle (\exists x)(x=\lnot y)}$.
    If the Gödel numbers replace the symbols, it becomes:${\displaystyle \{8,4,11,9,8,11,5,1,13,9\}}$.
    There are ten numbers, so the ten prime numbers are found and these are: ${\displaystyle \{2,3,5,7,11,13,17,19,23,29\}}$.
    Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving: ${\displaystyle 2^{8}\times 3^{4}\times 5^{11}\times 7^{9}\times 11^{8}\times 13^{11}\times 17^{5}\times 19^{1}\times 23^{13}\times 29^{9}}$.
    The resulting number is approximately ${\displaystyle 3.096262735\times 10^{78}}$.
87. The Klein–Gordon equation is:
    
    ${\displaystyle {\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi -\nabla ^{2}\psi +{\frac {m^{2}c^{2}}{\hbar ^{2}}}\psi =0.}$
88. The Dirac equation in the form originally proposed by Dirac is:
    
    ${\displaystyle \left(\beta mc^{2}+\sum _{k=1}^{3}\alpha _{k}p_{k}\,c\right)\psi (\mathbf {x} ,t)=i\hbar {\frac {\partial \psi (\mathbf {x} ,t)}{\partial t}}}$
    
    where, ψ = ψ(x, t) is the wave function for the electron, x and t are the space and time coordinates, m is the rest mass of the electron, p is the momentum, understood to be the momentum operator in the Schrödinger theory, c is the speed of light, and ħ = h/2π is the reduced Planck constant.
89. That is,
    
    ${\displaystyle \partial _{\mu }(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu })+\left({\frac {mc}{\hbar }}\right)^{2}A^{\nu }=0}$
90. The theorem applies more generally to any sufficiently strong formal system, showing that truth in the standard model of the system cannot be defined within the system.
91. Named to honor Voigt's 1898 work.
92. Named after Arthur Moritz Schoenflies
93. See Galois connections.
94. Oystein Ore would also write "Number Theory and Its History".
95. ${\displaystyle \langle \phi |\psi \rangle }$
96. That the scattering amplitude can be thought of as an analytic function of the angular momentum, and that the position of the poles determine power-law growth rates of the amplitude in the purely mathematical region of large values of the cosine of the scattering angle.
97. That is, ${\displaystyle \scriptstyle \Box }$
98. Also known as the d'Alembertian or wave operator.
99. Also known as, "permutation symbol" (see: permutation), "antisymmetric symbol" (see: antisymmetric), or "alternating symbol"
100. Note that "masses" (e.g., the coherent non-definite body shape) of particles are periodically reevaluated by the scientific community. The values may have been adjusted; adjustment by operations carried out on instruments in order that it provides given indications corresponding to given values of the measurand. In engineering, mathematics, and geodesy, the optimal parameter such estimation of a mathematical model so as to best fit a data set.
101. For the consensus, see Particle Data Group.
102. A locally defined set of four linearly independent vector fields called a tetrad
103. His usage of the Einstein summation was in order to offset the inconvenience in describing contractions and covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved.
104. See also: String theory landscape and Swampland
105. Devised by Joshua Lederberg and extended by Coxeter and Frucht
106. And, in 1938, Turing, A. M. (1938). "On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction". Proceedings of the London Mathematical Society. s2-43: 544–546. doi:10.1112/plms/s2-43.6.544..
107. Among von Neumann's other contributions include the application of operator theory to quantum mechanics, in the development of functional analysis, and on various forms of operator theory.

References and citations

General

• Florian Cajori (1929) A History of Mathematical Notations, 2 vols. Dover reprint in 1 vol., 1993. ISBN 0-486-67766-4.

Citations

1. Florian Cajori. A History of Mathematical Notations: Two Volumes in One. Cosimo, Inc., Dec 1, 2011
2. A Dictionary of Science, Literature, & Art, Volume 2. Edited by William Thomas Brande, George William Cox. Pg 683
3. "Notation – from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 24 June 2014.
4. Diophantos of Alexandria: A Study in the History of Greek Algebra. By Sir Thomas Little Heath. Pg 77.
5. Mathematics: Its Power and Utility. By Karl J. Smith. Pg 86.
6. The Commercial Revolution and the Beginnings of Western Mathematics in Renaissance Florence, 1300–1500. Warren Van Egmond. 1976. Page 233.
7. Solomon Gandz. "The Sources of al-Khowarizmi's Algebra"
8. Encyclopædia Americana. By Thomas Gamaliel Bradford. Pg 314
9. Mathematical Excursion, Enhanced Edition: Enhanced Webassign Edition By Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Cleg. Pg 186
10. Mathematics in Egypt and Mesopotamia
11. Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Mesopotamia" p. 25.
12. Duncan J. Melville (2003). Third Millennium Chronology, Third Millennium Mathematics. St. Lawrence University.
13. Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. pp. 30–31.
14. Heath (1931). "A Manual of Greek Mathematics". Nature. 128 (3235): 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0. S2CID 3994109.
15. Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who made mathematics a science."
16. The new encyclopædia; or, Universal dictionary of arts and sciences. By Encyclopaedia Perthensi. Pg 49
17. Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. p. 150. ISBN 0-02-318285-7. Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity.
18. "Archimedes of Syracuse". The MacTutor History of Mathematics archive. January 1999. Retrieved 9 June 2008.
19. O'Connor, J.J.; Robertson, E.F. (February 1996). "A history of calculus". University of St Andrews. Archived from the original on 15 July 2007. Retrieved 7 August 2007.
20. "Proclus' Summary". Gap.dcs.st-and.ac.uk. Archived from the original on 23 September 2015. Retrieved 24 June 2014.
21. Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", pp. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).
22. Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).
23. Mathematics and Measurement By Oswald Ashton Wentworth Dilk. Pg 14
24. A dictionary of science, literature and art, ed. by W.T. Brande. Pg 683
25. Boyer, Carl B. A History of Mathematics, 2nd edition, John Wiley & Sons, Inc., 1991.
26. Diophantine Equations. Submitted by: Aaron Zerhusen, Chris Rakes, & Shasta Meece. MA 330-002. Dr. Carl Eberhart. February 16, 1999.
27. A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 456
28. A History of Greek Mathematics: From Aristarchus to Diophantus. By Sir Thomas Little Heath. Pg 458
29. The American Mathematical Monthly, Volume 16. Pg 131
30. "Overview of Chinese mathematics". Groups.dcs.st-and.ac.uk. Retrieved 24 June 2014.
31. George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991, pp.140—148
32. Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, pp.428—437
33. "Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?". Psupress.psu.edu. Retrieved 24 June 2014.
34. Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd..
35. Sal Restivo
36. Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.
37. Marcel Gauchet, 151.
38. Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "China and India" p. 221. (cf., "he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India – or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words.")
39. Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
40. ""The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." – Pierre-Simon Laplace". History.mcs.st-and.ac.uk. Retrieved 24 June 2014.
41. A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
42. Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 230. (cf., "The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions.")
43. Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, pp. 263–77: "In a sense, Khwarizmi is more entitled to be called "the father of algebra" than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers".
44. Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "The Arabic Hegemony" p. 229. (cf., "It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation.")
45. Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. pp. 11–12. ISBN 0-7923-2565-6. OCLC 29181926.
46. Victor J. Katz (1998). History of Mathematics: An Introduction, pp. 255–59. Addison-Wesley. ISBN 0-321-01618-1.
47. F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.
48. Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3): 163–74. doi:10.1080/0025570X.1995.11996307.
49. Kunitzsch, Paul (2003), "The Transmission of Hindu-Arabic Numerals Reconsidered", in J. P. Hogendijk; A. I. Sabra (eds.), The Enterprise of Science in Islam: New Perspectives, MIT Press, pp. 3–22 (12–13), ISBN 978-0-262-19482-2
50. Marie-Thérèse d'Alverny, "Translations and Translators", pp. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
51. Guy Beaujouan, "The Transformation of the Quadrivium", pp. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
52. O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor History of Mathematics archive, University of St Andrews.
53. Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. p. 298. ISBN 0-393-04002-X.
54. O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews.
55. Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). "Revival and Decline of Greek Mathematics" p. 178 (cf., "The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation.")
56. Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) ISBN 0-521-32260-X.
57. Mathematical Magazine, Volume 1. Artemas Martin, 1887. Pg 124
58. Der Algorismus proportionum des Nicolaus Oresme: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Nicole Oresme. S. Calvary & Company, 1868.
59. Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 332–45, 382–91.
60. Later early modern version: A New System of Mercantile Arithmetic: Adapted to the Commerce of the United States, in Its Domestic and Foreign Relations with Forms of Accounts and Other Writings Usually Occurring in Trade. By Michael Walsh. Edmund M. Blunt (proprietor.), 1801.
61. Miller, Jeff (4 June 2006). "Earliest Uses of Symbols of Operation". Gulf High School. Retrieved 24 September 2006.
62. Arithmetical Books from the Invention of Printing to the Present Time. By Augustus De Morgan. p 2.
63. Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 0-393-32030-8.
64. Arithmetica integra. By Michael Stifel, Philipp Melanchton. Norimbergæ: Apud Iohan Petreium, 1544.
65. The History of Mathematics By Anne Roone. Pg 40
66. Memoirs of John Napier of Merchiston. By Mark Napier
67. An Account of the Life, Writings, and Inventions of John Napier, of Merchiston. By David Stewart Erskine Earl of Buchan, Walter Minto
68. Florian Cajori (1919). A History of Mathematics. Macmillan. p. 157.
69. Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 978-0-393-04002-9. pg 963–965,
70. Synopsis Palmariorum Matheseos. By William Jones. 1706. (Alt: Synopsis Palmariorum Matheseos: or, a New Introduction to the Mathematics. archive.org.)
71. When Less is More: Visualizing Basic Inequalities. By Claudi Alsina, Roger B. Nelse. Pg 18.
72. Euler, Leonhard, Solutio problematis ad geometriam situs pertinentis
73. The elements of geometry. By William Emerson
74. The Doctrine of Proportion, Arithmetical and Geometrical. Together with a General Method of Arening by Proportional Quantities. By William Emerson.
75. The Mathematical Correspondent. By George Baron. 83
76. Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Archived from the original on 10 September 2012. Retrieved 24 January 2012.
77. "Kramp biography". History.mcs.st-and.ac.uk. Retrieved 24 June 2014.
78. Mécanique analytique: Volume 1, Volume 2. By Joseph Louis Lagrange. Ms. Ve Courcier, 1811.
79. The collected mathematical papers of Arthur Cayley. Volume 11. Page 243.
80. Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1. By Ari Ben-Menahem. Pg 2070.
81. Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Originally at: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
82. The Words of Mathematics. By Steven Schwartzman. 6.
83. Electro-Magnetism: Theory and Applications. By A. Pramanik. 38
84. History of Nabla and Other Math Symbols. homepages.math.uic.edu/~hanson.
85. Hamilton, William Rowan (1854–1855). Wilkins, David R. (ed.). "On some Extensions of Quaternions" (PDF). Philosophical Magazine (7–9): 492–499, 125–137, 261–269, 46–51, 280–290. ISSN 0302-7597.
86. "James Clerk Maxwell". IEEE Global History Network. Retrieved 25 March 2013.
87. Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London. 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. S2CID 186207827. (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
88. Books I, II, III (1878) at the Internet Archive; Book IV (1887) at the Internet Archive
89. Cox, David A. (2012). Galois Theory. Pure and Applied Mathematics. 106 (2nd ed.). John Wiley & Sons. p. 348. ISBN 978-1118218426.
90. "TÜBİTAK ULAKBİM DergiPark". Journals.istanbul.edu.tr. Archived from the original on 16 March 2014. Retrieved 24 June 2014.
91. "Linear Algebra : Hussein Tevfik : Free Download & Streaming : Internet Archive". A.H. Boyajian. 1882. Retrieved 24 June 2014.
92. Ricci Curbastro, G. (1892). "Résumé de quelques travaux sur les systèmes variables de fonctions associés à une forme différentielle quadratique". Bulletin des Sciences Mathématiques. 2 (16): 167–189.
93. Voigt, Woldemar (1898). Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Leipzig: Von Veit.
94. Poincaré, Henri, "Analysis situs", Journal de l'École Polytechnique ser 2, 1 (1895) pp. 1–123
95. Whitehead, John B., Jr. (1901). "Review: Alternating Current Phenomena, by C. P. Steinmetz" (PDF). Bull. Amer. Math. Soc. 7 (9): 399–408. doi:10.1090/s0002-9904-1901-00825-7.
96. There are many editions. Here are two:
    • (French) Published 1901 by Gauthier-Villars, Paris. 230p. OpenLibrary OL15255022W, PDF.
    • (Italian) Published 1960 by Edizione cremonese, Roma. 463p. OpenLibrary OL16587658M.
97. Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen, Springer, 54 (1–2): 125–201, doi:10.1007/BF01454201, S2CID 120009332
98. Zermelo, Ernst (1904). "Beweis, dass jede Menge wohlgeordnet werden kann" (reprint). Mathematische Annalen. 59 (4): 514–16. doi:10.1007/BF01445300. S2CID 124189935.
99. On the Dynamics of the Electron (July)  – via Wikisource.
100. Fréchet, Maurice, "Sur quelques points du calcul fonctionnel", PhD dissertation, 1906
101. Cuthbert Edmund Cullis (Author) (5 June 2011). "Matrices and determinoids Volume 2: Cuthbert Edmund Cullis: Amazon.com: Books". Retrieved 24 June 2014.
102. Can be assigned a given matrix: About a class of matrices. (Gr. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) by Isay Schur
103. An Introduction To The Modern Theory Of Equations. By Florian Cajori.
104. Proceedings of the Prussian Academy of Sciences (1918). Pg 966.
105. Sitzungsberichte der Preussischen Akademie der Wissenschaften (1918) (Tr. Proceedings of the Prussian Academy of Sciences (1918)). archive.org; See also: Kaluza–Klein theory.
106. J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85–86, §3.5. ISBN 0-7167-0344-0.
107. R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
108. Schouten, Jan A. (1924). R. Courant (ed.). Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimmensional differential geometry). Grundlehren der mathematischen Wissenschaften (in German). 10. Berlin: Springer Verlag.
109. Robert B. Ash. A Primer of Abstract Mathematics. Cambridge University Press, Jan 1, 1998
110. The New American Encyclopedic Dictionary. Edited by Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford. Pg 34
111. The Mathematical Principles of Natural Philosophy, Volume 1. By Sir Isaac Newton, John Machin. Pg 12.
112. In The Scientific Outlook (1931)
113. Mathematics simplified and made attractive: or, The laws of motion explained. By Thomas Fisher. Pg 15. (cf. But an abstraction not founded upon, and not consonant with Nature and (Logical) Truth, would be a falsity, an insanity.)
114. Proposition VI, On Formally Undecidable Propositions in Principia Mathematica and Related Systems I (1931)
115. Casti, John L. 5 Golden Rules. New York: MJF Books, 1996.
116. Gr. Methoden Der Mathematischen Physik
117. P.A.M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
118. E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87–132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
119. F. Bloch; A. Nordsieck (1937). "Note on the Radiation Field of the Electron". Physical Review. 52 (2): 54–59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
120. V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56 (1): 72–85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
121. R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461–477. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
122. Van der Waerden B.L. (1929). "Spinoranalyse". Nachr. Ges. Wiss. Göttingen Math.-Phys. 1929: 100–109.
123. Veblen O. (1933). "Geometry of two-component Spinors". Proc. Natl. Acad. Sci. USA. 19 (4): 462–474. Bibcode:1933PNAS...19..462V. doi:10.1073/pnas.19.4.462. PMC 1086023. PMID 16577541.
124. PAM Dirac (1939). "A new notation for quantum mechanics". Mathematical Proceedings of the Cambridge Philosophical Society. 35 (3). pp. 416–418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162.
125. H. Grassmann (1862). Extension Theory. History of Mathematics Sources. American Mathematical Society, London Mathematical Society, 2000 translation by Lloyd C. Kannenberg.
126. Steven Weinberg (1964), The quantum theory of fields, Volume 2, Cambridge University Press, 1995, p. 358, ISBN 0-521-55001-7
127. "The Nobel Prize in Physics 1965". Nobel Foundation. Retrieved 9 October 2008.
128. S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.
129. S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.
130. A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.
131. F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.
132. P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.
133. G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
134. http://www.physics.drexel.edu/~vkasli/phys676/Notes%20for%20a%20brief%20history%20of%20quantum%20gravity%20-%20Carlo%20Rovelli.pdf
135. Bourbaki, Nicolas (1972). "Univers". In Michael Artin; Alexandre Grothendieck; Jean-Louis Verdier (eds.). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Lecture notes in mathematics 269) (in French). Berlin; New York: Springer-Verlag. pp. 185–217.
136. F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.
137. F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.
138. F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.
139. D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Retrieved 8 May 2008.
140. "Mainpage".
141. Candelas, P. (1985). "Vacuum configurations for superstrings". Nuclear Physics B. 258: 46–74. Bibcode:1985NuPhB.258...46C. doi:10.1016/0550-3213(85)90602-9.
142. De Felice, F.; Clarke, C.J.S. (1990), Relativity on Curved Manifolds, p. 133
143. "Quantum invariants of knots and 3-manifolds" by V. G. Turaev (1994), page 71
144. Pisanski, Tomaž; Servatius, Brigitte (2013), "2.3.2 Cubic graphs and LCF notation", Configurations from a Graphical Viewpoint, Springer, p. 32, ISBN 9780817683641
145. Frucht, R. (1976), "A canonical representation of trivalent Hamiltonian graphs", Journal of Graph Theory, 1 (1): 45–60, doi:10.1002/jgt.3190010111
146. Fraleigh 2002:89; Hungerford 1997:230
147. Dehn, Edgar. Algebraic Equations, Dover. 1930:19
148. "The IBM 601 Multiplying Punch". Columbia.edu. Retrieved 24 June 2014.
149. "Interconnected Punched Card Equipment". Columbia.edu. 24 October 1935. Retrieved 24 June 2014.
150. Proceedings of the London Mathematical Society 42 (2)
151. Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.

Further reading

General

• A Short Account of the History of Mathematics. By Walter William Rouse Ball.
• A Primer of the History of Mathematics. By Walter William Rouse Ball.
• A History of Elementary Mathematics: With Hints on Methods of Teaching. By Florian Cajori.
• A History of Elementary Mathematics. By Florian Cajori.
• A History of Mathematics. By Florian Cajori.
• A Short History of Greek Mathematics. By James Gow.
• On the Development of Mathematical Thought During the Nineteenth Century. By John Theodore Merz.
• A New Mathematical and Philosophical Dictionary. By Peter Barlow.
• Historical Introduction to Mathematical Literature. By George Abram Miller
• A Brief History of Mathematics. By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
• History of Modern Mathematics. By David Eugene Smith.
• History of modern mathematics. By David Eugene Smith, Mansfield Merriman.

Other

• Principia Mathematica, Volume 1 & Volume 2. By Alfred North Whitehead, Bertrand Russell.
• The Mathematical Principles of Natural Philosophy, Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
• General investigations of curved surfaces of 1827 and 1825. By Carl Friedrich Gaus.

External links

• Mathematical Notation: Past and Future
• History of Mathematical Notation
• Earliest Uses of Mathematical Notation
• Finger counting. files.chem.vt.edu.
• Some Common Mathematical Symbols and Abbreviations (with History). Isaiah Lankham, Bruno Nachtergaele, Anne Schilling.