Gammatone filter

A gammatone filter is a linear filter described by an impulse response that is the product of a gamma distribution and sinusoidal tone. It is a widely used model of auditory filters in the auditory system.

A gammatone impulse response

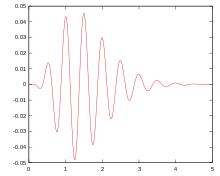
The gammatone impulse response is given by

where (in Hz) is the center frequency, (in radians) is the phase of the carrier, is the amplitude, is the filter's order, (in Hz) is the filter's bandwidth, and (in seconds) is time.

This is a sinusoid (a pure tone) with an amplitude envelope which is a scaled gamma distribution function.[1]

Different ways of motivating the gammatone filter for auditory processing have been presented by Johannesma,[2] Patterson et al.,[3] Hewitt and Meddis,[4] and Lindeberg and Friberg.[5]

Variations

Variations and improvements of the gammatone model of auditory filtering include the gammachirp filter, the all-pole and one-zero gammatone filters, the two-sided gammatone filter, and filter cascade models, and various level-dependent and dynamically nonlinear versions of these.[6]

References
  1. Slaney, Malcolm (1993). "An Efficient Implementation of the Patterson–Holdsworth Auditory Filter Bank" (PDF). Apple Computer Technical Report #35.
  2. P. I. M. Johannesma (1972). "The pre-response stimulus ensemble of neurons in the cochlear nucleus". IPO Symposium on Hearing Theory. Eindhoven, The Netherlands. pp. 58–69.
  3. R. D. Patterson, I. Nimmo-Smith, J. Holdsworth and P. Rice (1987). "An efficient auditory filterbank based on the gammatone function". A meeting of the IOC Speech Group on Auditory Modelling at RSRE. 2 (7).CS1 maint: multiple names: authors list (link)
  4. M. J. Hewitt and R. Meddis (1994). "A computer model of amplitude-modulation sensitivity of single units in the inferior colliculus". The Journal of the Acoustical Society of America. 95. pp. 2145–2159. doi:10.1121/1.408676.
  5. T. Lindeberg and A. Friberg (2015). "Idealized computational models for auditory receptive fields". PLoS ONE. 10 (3). pp. e0119032. doi:10.1371/journal.pone.0119032.
  6. Richard F. Lyon; Andreas G. Katsiamis; Emmanuel M. Drakakis (2010). "History and Future of Auditory Filter Models" (PDF). Proc. ISCAS. IEEE.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.