Fuhrmann circle
In geometry, the Fuhrmann circle of a triangle, named after the German Wilhelm Fuhrmann (1833–1904), is the circle with a diameter of the line segment between the orthocenter and the Nagel point . This circle is identical with the circumcircle of the Fuhrmann triangle.[1]
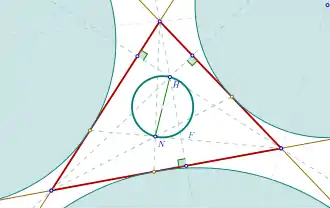
Fuhrmann circle

Fuhrmann circle with Fuhrmann triangle (red),
Nagel point and orthocenter
Nagel point and orthocenter
The radius of the Fuhrmann circle of a triangle with sides a, b, and c and circumradius R is
which is also the distance between the circumcenter and incenter.[2]
Aside from the orthocenter the Fuhrmann circle intersects each altitude of the triangle in one additional point. Those points all have the distance from their associated vertices of the triangle. Here denotes the radius of the triangles incircle.[3]
Notes
- Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, pp. 228–229, 300 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- Weisstein, Eric W. "Fuhrmann Circle". MathWorld.
- Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 49-52
Further reading
- Nguyen Thanh Dung: "The Feuerbach Point and the Fuhrmann Triangle". Forum Geometricorum, Volume 16 (2016), pp. 299–311.
- J. A. Scott: An Eight-Point Circle. In: The Mathematical Gazette, Volume 86, No. 506 (Jul., 2002), pp. 326–328 (JSTOR)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.