Frank-Kamenetskii theory

In combustion, Frank-Kamenetskii theory explains the thermal explosion of a homogeneous mixture of reactants, kept inside a closed vessel with constant temperature walls. It is named after a Russian scientist David A. Frank-Kamenetskii, who along with Nikolay Semenov developed the theory in the 1930s.[1][2][3][4]

Problem description[5][6][7][8][9]

Consider a vessel maintained at a constant temperature ${\displaystyle T_{o}}$, containing a homogeneous reacting mixture. Let the characteristic size of the vessel be ${\displaystyle a}$. Since the mixture is homogeneous, the density ${\displaystyle \rho }$ is constant. During the initial period of ignition, the consumption of reactant concentration is negligible (see ${\displaystyle t_{f}}$ and ${\displaystyle t_{e}}$ below), thus the explosion is governed only by the energy equation. Assuming a one-step global reaction ${\displaystyle {\text{fuel}}+{\text{oxidizer}}\rightarrow {\text{products}}+q}$, where ${\displaystyle q}$ is the amount of heat released per unit mass of fuel consumed, and reaction rate governed by Arrhenius law, the energy equation becomes

${\displaystyle \rho c_{v}{\frac {\partial T}{\partial t}}=\lambda \nabla ^{2}T+q\rho BY_{Fo}e^{-E/(RT)}}$

where

• ${\displaystyle T}$ is the temperature of the mixture
• ${\displaystyle c_{v}}$ is the specific heat at constant volume
• ${\displaystyle \lambda }$ is the thermal conductivity
• ${\displaystyle B}$ is the pre-exponential factor with dimension of one over time
• ${\displaystyle Y_{Fo}}$ is the initial fuel mass fraction
• ${\displaystyle E}$ is the activation energy
• ${\displaystyle R}$ is the universal gas constant

Non-dimensionalization

The non-dimensional activation energy ${\displaystyle \beta }$ and the heat-release parameter ${\displaystyle \gamma }$ are

${\displaystyle \beta ={\frac {E}{RT_{o}}},\quad \gamma ={\frac {qY_{Fo}}{c_{v}T_{o}}}}$

The characteristic heat conduction time across the vessel is ${\displaystyle t_{c}=\rho c_{v}a^{2}/\lambda }$, the characteristic fuel consumption time is ${\displaystyle t_{f}=\left(Be^{-\beta }\right)^{-1}}$ and the characteristic explosion/ignition time is ${\displaystyle t_{e}=\left(\beta \gamma Be^{-\beta }\right)^{-1}}$. Note should be made that in combustion process, typically ${\displaystyle \gamma \approx 6{-}8,\ \beta \approx 30{-}100}$ so that ${\displaystyle \beta \gamma \gg 1}$. Therefore, ${\displaystyle t_{f}=\beta \gamma t_{e}\gg 1}$, i.e., the fuel is consumed at much longer times when compared with ignition time, the fuel consumption is essentially negligible to study ignition/explosion. That is the reason the fuel concentration is assumed to same as the initial fuel concentration ${\displaystyle Y_{Fo}}$. The non-dimensional scales are

${\displaystyle \tau ={\frac {t}{t_{e}}},\quad \theta ={\frac {\beta (T-T_{o})}{T_{o}}},\quad \eta ^{j}={\frac {r^{j}}{a}},\quad \delta ={\frac {t_{c}}{t_{e}}}}$

where ${\displaystyle \delta }$ is the Damköhler number and ${\displaystyle r}$ is the spatial coordinate with origin at the center, ${\displaystyle j=0}$ for planar slab, ${\displaystyle j=1}$ for cylindrical vessel and ${\displaystyle j=2}$ for spherical vessel. With this scale, the equation becomes

${\displaystyle {\frac {\partial \theta }{\partial \tau }}={\frac {1}{\delta }}{\frac {1}{\eta ^{j}}}{\frac {\partial }{\partial \eta }}\left(\eta ^{j}{\frac {\partial \theta }{\partial \eta }}\right)+e^{\theta /(1+\theta /\beta )}}$

Since ${\displaystyle \beta \gg 1}$, the exponential term can be linearized ${\displaystyle e^{\theta /(1+\theta /\beta )}\approx e^{\theta }}$, hence

${\displaystyle {\frac {\partial \theta }{\partial \tau }}={\frac {1}{\delta }}{\frac {1}{\eta ^{j}}}{\frac {\partial }{\partial \eta }}\left(\eta ^{j}{\frac {\partial \theta }{\partial \eta }}\right)+e^{\theta }}$

Semenov theory

Before Frank-Kamenetskii, his doctoral advisor Nikolay Semyonov (or Semenov) proposed a thermal explosion theory with a simple model i.e., he assumed a linear function for heat conduction process instead of Laplacian operator. Semenov's equation reads as

${\displaystyle {\frac {\partial \theta }{\partial \tau }}=e^{\theta }-{\frac {\theta }{\delta }},\quad \theta (0)=0}$

For ${\displaystyle e^{-1}<\delta <\infty }$, the system explodes since the exponential term dominates. For ${\displaystyle 0<\delta <e^{-1}}$, the system goes to a steady state, the system doesn't explode. In particular, Semenov found the critical Damköhler number, which is called as Frank-Kamenetskii parameter ${\displaystyle \delta _{c}=e^{-1}}$(where ${\displaystyle \theta =1}$) as a critical point where the system changes from steady state to explosive state. For ${\displaystyle \delta \gg 1}$, the solution is

${\displaystyle {\frac {\partial \theta }{\partial \tau }}=e^{\theta },\quad \Rightarrow \quad \theta =\ln \left({\frac {1}{1-\tau }}\right)}$

At time ${\displaystyle \tau =1}$, the system explodes. This time is also referred to as the adiabatic induction period since heat conduction is negligible here.

Frank-Kamenetskii steady-state theory[10][11]

The only parameter which characterizes the explosion is the Damköhler number ${\displaystyle \delta }$. When ${\displaystyle \delta }$ is very high, conduction time is longer than the chemical reaction time and the system explodes with high temperature since there is not enough time for conduction to remove the heat. On the other hand, when ${\displaystyle \delta }$ is very low, heat conduction time is much faster than the chemical reaction time, such that all the heat produced by the chemical reaction is immediately conducted to the wall, thus there is no explosion, it goes to an almost steady state, Amable Liñán coined this mode as slowly reacting mode. At a critical Damköhler number ${\displaystyle \delta _{c}}$ the system goes from slowly reacting mode to explosive mode. Therefore, ${\displaystyle \delta <\delta _{c}}$, the system is in steady state. Instead of solving the full problem to find this ${\displaystyle \delta _{c}}$, Frank-Kamenetskii solved the steady state problem for various Damköhler number until the critical value, beyond which no steady solution exists. So the problem to be solved is

${\displaystyle {\frac {1}{\eta ^{j}}}{\frac {d}{d\eta }}\left(\eta ^{j}{\frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

with boundary conditions

${\displaystyle \theta (1)=0,\quad {\frac {d\theta }{d\eta }}_{\eta =0}=0}$

the second condition is due to the symmetry of the vessel. The above equation is special case of Liouville–Bratu–Gelfand equation in mathematics.

Planar vessel

Frank-Kamenetskii explosion for planar vessel

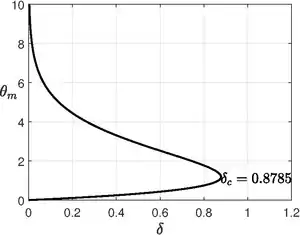
For planar vessel, there is an exact solution. Here ${\displaystyle j=0}$, then

${\displaystyle {\frac {d^{2}\theta }{d\eta ^{2}}}=-\delta e^{\theta }}$

If the transformations ${\displaystyle \Theta =\theta _{m}-\theta }$ and ${\displaystyle \xi ^{2}=\delta e^{\theta _{m}}\eta ^{2}}$, where ${\displaystyle \theta _{m}}$ is the maximum temperature which occurs at ${\displaystyle \eta =0}$ due to symmetry, are introduced

${\displaystyle {\frac {d^{2}\Theta }{d\xi ^{2}}}=e^{-\Theta },\quad \Theta (0)=0,\quad {\frac {d\Theta }{d\xi }}_{\xi =0}=0}$

Integrating once and using the second boundary condition, the equation becomes

${\displaystyle {\frac {d\Theta }{d\xi }}={\sqrt {2(1-e^{-\Theta })}}}$

and integrating again

${\displaystyle e^{(\theta _{m}-\theta )/2}=\cosh \left({\sqrt {\frac {\delta e^{\theta _{m}}}{2}}}\eta \right)}$

The above equation is the exact solution, but ${\displaystyle \theta _{m}}$ maximum temperature is unknown, but we have not used the boundary condition of the wall yet. Thus using the wall boundary condition ${\displaystyle \theta =0}$ at ${\displaystyle \eta =1}$, the maximum temperature is obtained from an implicit expression,

${\displaystyle e^{\theta _{m}/2}=\cosh \left({\sqrt {\frac {\delta e^{\theta _{m}}}{2}}}\right)\quad {\text{or}}\quad \delta =2e^{-\theta _{m}}\left(\cosh ^{-1}e^{\theta _{m}/2}\right)^{2}}$

Critical ${\displaystyle \delta _{c}}$ is obtained by finding the maximum point of the equation (look figure), i.e., ${\displaystyle d\delta /d\theta _{m}=0}$ at ${\displaystyle \delta _{c}}$.

${\displaystyle {\frac {d\delta }{d\theta _{m}}}=0,\quad \Rightarrow \quad e^{\theta _{m,c}/2}-{\sqrt {e^{\theta _{m,c}}-1}}\cosh ^{-1}e^{\theta _{m,c}/2}=0}$

${\displaystyle \theta _{m,c}=1.1868,\quad \Rightarrow \quad \delta _{c}=0.8785}$

So the critical Frank-Kamentskii parameter is ${\displaystyle \delta _{c}=0.8785}$. The system has no steady state( or explodes) for ${\displaystyle \delta >\delta _{c}=0.8785}$ and for ${\displaystyle \delta <\delta _{c}=0.8785}$, the system goes to a steady state with very slow reaction.

Cylindrical vessel

Frank-Kamenetskii explosion for cylindrical vessel

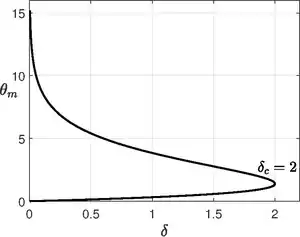
For cylindrical vessel, there is an exact solution. Though Frank-Kamentskii used numerical integration assuming there is no explicit solution, Paul L. Chambré provided an exact solution in 1952.[12] H. Lemke also solved provided a solution in a somewhat different form in 1913.[13] Here ${\displaystyle j=1}$, then

${\displaystyle {\frac {1}{\eta }}{\frac {d}{d\eta }}\left(\eta {\frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

If the transformations ${\displaystyle \omega =\eta d\theta /d\eta }$ and ${\displaystyle \chi =e^{\theta }\eta ^{2}}$ are introduced

${\displaystyle {\frac {d\omega }{d\chi }}=-{\frac {\delta }{2+\omega }},\quad \omega (0)=0}$

The general solution is ${\displaystyle \omega ^{2}+4\omega +C=-2\delta \chi }$. But ${\displaystyle C=0}$ from the symmetry condition at the centre. Writing back in original variable, the equation reads,

${\displaystyle \eta ^{2}\left({\frac {d\theta }{d\eta }}\right)^{2}+4\eta {\frac {d\theta }{d\eta }}=-2\delta \eta ^{2}e^{\theta }}$

But the original equation multiplied by ${\displaystyle 2\eta ^{2}}$ is

${\displaystyle 2\eta ^{2}{\frac {d^{2}\theta }{d\eta ^{2}}}+2\eta {\frac {d\theta }{d\eta }}=-2\delta \eta ^{2}e^{\theta }}$

Now subtracting the last two equation from one another leads to

${\displaystyle {\frac {d^{2}\theta }{d\eta ^{2}}}-{\frac {1}{\eta }}{\frac {d\theta }{d\eta }}-{\frac {1}{2}}\left({\frac {d\theta }{d\eta }}\right)^{2}=0}$

This equation is easy to solve because it involves only the derivatives, so letting ${\displaystyle g(\eta )=d\theta /d\eta }$ transforms the equation

${\displaystyle {\frac {dg}{d\eta }}-{\frac {g}{\eta }}-{\frac {g^{2}}{2}}=0}$

This is a Bernoulli differential equation of order ${\displaystyle 2}$, a type of Riccati equation. The solution is

${\displaystyle g(\eta )={\frac {d\theta }{d\eta }}=-{\frac {4\eta }{B'+\eta ^{2}}}}$

Integrating once again, we have ${\displaystyle \theta =A-2\ln(B\eta ^{2}+1)}$ where ${\displaystyle B=1/B'}$. We have used already one boundary condition, there is one more boundary condition left, but with two constants ${\displaystyle A,\ B}$. It turns out ${\displaystyle A}$ and ${\displaystyle B}$ are related to each other, which is obtained by substituting the above solution into the starting equation we arrive at ${\displaystyle A=\ln(8B/\delta )}$. Therefore, the solution is

${\displaystyle \theta =\ln \left[{\frac {8B/\delta }{(B\eta ^{2}+1)^{2}}}\right]}$

Now if we use the other boundary condition ${\displaystyle \theta (1)=0}$, we get an equation for ${\displaystyle B}$ as ${\displaystyle \delta (B+1)^{2}-8B=0}$. The maximum value of ${\displaystyle \delta }$ for which solution is possible is when ${\displaystyle B=1}$, so the critical Frank-Kamentskii parameter is ${\displaystyle \delta _{c}=2}$. The system has no steady state( or explodes) for ${\displaystyle \delta >\delta _{c}=2}$ and for ${\displaystyle \delta <\delta _{c}=2}$, the system goes to a steady state with very slow reaction. The maximum temperature ${\displaystyle \theta _{m}}$ occurs at ${\displaystyle \eta =0}$

${\displaystyle \theta _{m}=\ln \left({\frac {8B}{\delta }}\right)\quad {\text{or}}\quad \delta =8Be^{-\theta _{m}}}$

For each value of ${\displaystyle \delta }$, we have two values of ${\displaystyle \theta _{m}}$ since ${\displaystyle B}$ is multi-valued. The maximum critical temperature is ${\displaystyle \theta _{m,c}=\ln 4}$.

Spherical vessel

For spherical vessel, there is no known explicit solution, so Frank-Kamenetskii used numerical methods to find the critical value. Here ${\displaystyle j=2}$, then

${\displaystyle {\frac {1}{\eta ^{2}}}{\frac {d}{d\eta }}\left(\eta ^{2}{\frac {d\theta }{d\eta }}\right)=-\delta e^{\theta }}$

If the transformations ${\displaystyle \Theta =\theta _{m}-\theta }$ and ${\displaystyle \xi ^{2}=\delta e^{\theta _{m}}\eta ^{2}}$, where ${\displaystyle \theta _{m}}$ is the maximum temperature which occurs at ${\displaystyle \eta =0}$ due to symmetry, are introduced

${\displaystyle {\frac {1}{\xi ^{2}}}{\frac {d}{d\xi }}\left(\xi ^{2}{\frac {d\Theta }{d\xi }}\right)=e^{-\Theta },\quad \Theta (0)=0,\quad {\frac {d\Theta }{d\xi }}_{\xi =0}=0}$

The above equation is nothing but Emden–Chandrasekhar equation,[14] which appears in astrophysics describing isothermal gas sphere. Unlike planar and cylindrical case, the spherical vessel has infinitely many solutions for ${\displaystyle \delta <\delta _{c}}$ oscillating about the point ${\displaystyle \delta =2}$,[15] instead of just two solutions, which was shown by Israel Gelfand.[16] The lowest branch will be chosen to explain explosive behavior.

From numerical solution, it is found that the critical Frank-Kamenetskii parameter is ${\displaystyle \delta _{c}=3.32}$. The system has no steady state( or explodes) for ${\displaystyle \delta >\delta _{c}=3.32}$ and for ${\displaystyle \delta <\delta _{c}=3.32}$, the system goes to a steady state with very slow reaction. The maximum temperature ${\displaystyle \theta _{m}}$ occurs at ${\displaystyle \eta =0}$ and maximum critical temperature is ${\displaystyle \theta _{m,c}=1.61}$.

Non-symmetric geometries

For vessels which are not symmetric about the center (for example rectangular vessel), the problem involves solving a nonlinear partial differential equation instead of a nonlinear ordinary differential equation, which can be solved only through numerical methods in most cases. The equation is

${\displaystyle \nabla ^{2}\theta +\delta e^{\theta }=0}$

with boundary condition ${\displaystyle \theta =0}$ on the bounding surfaces.

Applications

Since the model assumes homogeneous mixture, the theory is well applicable to study the explosive behavior of solid fuels (spontaneous ignition of bio fuels, organic materials, garbage, etc.,). This is also used to design explosives and fire crackers. The theory predicted critical values accurately for low conductivity fluids/solids with high conductivity thin walled containers.[17]

See also

• Clarke's equation

References

1. Frank-Kamenetskii, David A. "Towards temperature distributions in a reaction vessel and the stationary theory of thermal explosion." Doklady Akademii Nauk SSSR. Vol. 18. 1938.
2. Frank-Kamenetskii, D. A. "Calculation of thermal explosion limits." Acta. Phys.-Chim USSR 10 (1939): 365.
3. Semenov, N. N. "The calculation of critical temperatures of thermal explosion." Z Phys Chem 48 (1928): 571.
4. Semenov, N. N. "On the theory of combustion processes." Z. phys. Chem 48 (1928): 571–582.
5. Frank-Kamenetskii, David Albertovich. Diffusion and heat exchange in chemical kinetics. Princeton University Press, 2015.
6. Linan, Amable, and Forman Arthur Williams. "Fundamental aspects of combustion." (1993).
7. Williams, Forman A. "Combustion theory." (1985).
8. Buckmaster, John David, and Geoffrey Stuart Stephen Ludford. Theory of laminar flames. Cambridge University Press, 1982.
9. Buckmaster, John D., ed. The mathematics of combustion. Society for Industrial and Applied Mathematics, 1985.
10. Zeldovich, I. A., Barenblatt, G. I., Librovich, V. B., and Makhviladze, G. M. (1985). Mathematical theory of combustion and explosions.
11. Lewis, Bernard, and Guenther Von Elbe. Combustion, flames and explosions of gases. Elsevier, 2012.
12. Chambre, P. L. "On the Solution of the Poisson‐Boltzmann Equation with Application to the Theory of Thermal Explosions." The Journal of Chemical Physics 20.11 (1952): 1795–1797.
13. Lemke, H. (1913). Über die Differentialgleichungen, welche den Gleichgewichtszustand eines gasförmigem Himmelskörpers bestimmen, dessen Teile gegeneinander nach dem Newtonschen Gesetz gravitieren. Journal für die reine und angewandte Mathematik, 142, 118-145.
14. Subrahmanyan Chandrasekhar. An introduction to the study of stellar structure. Vol. 2. Courier Corporation, 1958.
15. Jacobsen, Jon, and Klaus Schmitt. "The Liouville–Bratu–Gelfand problem for radial operators." Journal of Differential Equations 184.1 (2002): 283–298.
16. Gelfand, I. M. (1963). Some problems in the theory of quasilinear equations. Amer. Math. Soc. Transl, 29(2), 295–381.
17. Zukas, Jonas A., William Walters, and William P. Walters, eds. Explosive effects and applications. Springer Science & Business Media, 2002.

External links

• The Frank-Kamenetskii problem in Wolfram solver http://demonstrations.wolfram.com/TheFrankKamenetskiiProblem/
• Tracking the Frank-Kamenetskii Problem in Wolfram solver http://demonstrations.wolfram.com/TrackingTheFrankKamenetskiiProblem/
• Planar solution in Chebfun solver http://www.chebfun.org/examples/ode-nonlin/BlowupFK.html