Fish curve
A fish curve is an ellipse negative pedal curve that is shaped like a fish. In a fish curve, the pedal point is at the focus for the special case of the squared eccentricity .[1] The parametric equations for a fish curve correspond to those of the associated ellipse.
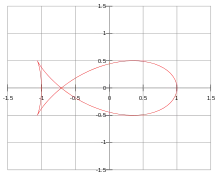
Equations
For an ellipse with the parametric equations
the corresponding fish curve has parametric equations
When the origin is translated to the node (the crossing point), the Cartesian equation can be written as:[2][3]
Area
The area of a fish curve is given by:
,
so the area of the tail and head are given by:
giving the overall area for the fish as:
.[2]
Curvature, arc length, and tangential angle
The arc length of the curve is given by .
The curvature of a fish curve is given by:
,
and the tangential angle is given by:
where is the complex argument.
References
- Lockwood, E. H. (1957). "Negative Pedal Curve of the Ellipse with Respect to a Focus". Math. Gaz. 41: 254–257.
- Weisstein, Eric W. "Fish Curve". MathWorld. Retrieved May 23, 2010.
- Lockwood, E. H. (1967). A Book of Curves. Cambridge, England: Cambridge University Press. p. 157.