Euclid's orchard

In mathematics, informally speaking, Euclid's orchard is an array of one-dimensional "trees" of unit height planted at the lattice points in one quadrant of a square lattice.[1] More formally, Euclid's orchard is the set of line segments from (i, j, 0) to (i, j, 1), where i and j are positive integers.

Plan view of one corner of Euclid's orchard. Trees marked by a solid blue dot are visible from the origin.

Perspective view of Euclid's orchard from the origin. Red trees denote rows two off the main diagonal.

One corner of Euclid's orchard, in which trees are labelled with the x co-ordinate of their projection on the plane x + y = 1.

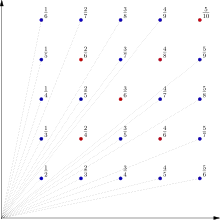
The trees visible from the origin are those at lattice points (m, n, 0), where m and n are coprime, i.e., where the fraction m/n is in reduced form. The name Euclid's orchard is derived from the Euclidean algorithm.

If the orchard is projected relative to the origin onto the plane x + y = 1 (or, equivalently, drawn in perspective from a viewpoint at the origin) the tops of the trees form a graph of Thomae's function. The point (m, n, 1) projects to

${\displaystyle \left({\frac {m}{m+n}},{\frac {n}{m+n}},{\frac {1}{m+n}}\right).}$

See also

• Opaque forest problem

References

1. Weisstein, Eric W. "Euclid's Orchard". MathWorld.

External links

• Euclid's Orchard, Grade 9-11 activities and problem sheet, Texas Instruments Inc.
• Project Euler related problem