Eduard Weyr

Eduard Weyr (June 22, 1852 – July 23, 1903) was a Czech mathematician now chiefly remembered as the discoverer of a certain canonical form for square matrices over algebraically closed fields.[1][2] Weyr presented this form briefly in a paper published in 1885.[3] He followed it up with a more elaborate treatment in a paper published in 1890.[4] This particular canonical form has been named as the Weyr canonical form in a paper by Shapiro published in The American Mathematical Monthly in 1999.[5] Previously, this form has been variously called as modified Jordan form, reordered Jordan form, second Jordan form, and H-form.[6]

Eduard Weyr

Weyr's father was a mathematician at a secondary school in Prague, and his older brother, Emil Weyr, was also a mathematician. Weyr studied at Prague Polytechnic and Charles-Ferdinand University in Prague. He received his doctorate from the University of Göttingen in 1873 with dissertation Über algebraische Raumcurven.[7] After a short spell in Paris studying under Charles Hermite and Joseph Alfred Serret, he returned to Prague where he eventually became a professor at Charles-Ferdinand University. Weyr also published research in geometry, in particular projective and differential geometry.[1] In 1893 in Chicago, his paper Sur l'équation des lignes géodésiques was read (but not by him) at the International Congress of Mathematicians held in connection with the World's Columbian Exposition.[8]

Weyr canonical form

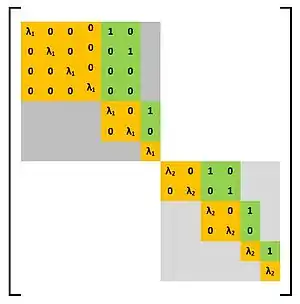
The image shows an example of a general Weyr matrix consisting of two blocks each of which is a basic Weyr matrix. The basic Weyr matrix in the top-left corner has the structure (4,2,1) and the other one has the structure (2,2,1,1).

References
  1. Kevin C. Meara; John Clark; Charles I. Vinsonhaler (2011). Advanced Topics in Linear Algebra: Weaving Matrix Problems through the Weyr Form. Oxford University Press. pp. 94–95.
  2. O'Connor, John J.; Robertson, Edmund F., "Eduard Weyr", MacTutor History of Mathematics archive, University of St Andrews.
  3. Eduard Weyr (1885). "Répartition des matrices en espèces et formation de toutes les espèces" (PDF). Comptes Rendus, Paris. 100: 966–969. Retrieved 10 December 2013.
  4. Eduard Weyr (1890). "Zur Theorie der bilinearen Formen". Monatshefte für Mathematik und Physik. 1: 163–236.
  5. Shapiro, H. (1999). "The Weyr characteristic". American Mathematical Monthly. 106 (10): 919–929. doi:10.2307/2589746. JSTOR 2589746.
  6. Kevin C. Meara; John Clark; Charles I. Vinsonhaler (2011). Advanced Topics in Linear Algebra: Weaving Matrix Problems through the Weyr Form. Oxford University Press. pp. 44, 81–82.
  7. Eduard Weyr at the Mathematics Genealogy Project
  8. "Sur l'équation des lignes géodésiques par M. Edouard Weyr". Mathematical papers read at the International Mathematical Congress held in connection with the World's Columbian Exposition. NY: Macmillan as publisher for the AMS. 1896. pp. 408–411.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.