Diffiety

In mathematics, a diffiety (/dəˈfaɪəˌtiː/) is a geometrical object introduced by Alexandre Mikhailovich Vinogradov (see Vinogradov (1984a) harvtxt error: no target: CITEREFVinogradov1984a (help)) playing the same role in the modern theory of partial differential equations as algebraic varieties play for algebraic equations.

Definition

To define a diffiety, we need to take a geometric approach to the description of differential equations and their solutions. This requires the notions of jet spaces, prolongation, and Cartan distribution which will be introduced below. The reader familiar with those notions can directly proceed to the definition.

Jet Spaces

Let ${\displaystyle E}$ be an ${\displaystyle m+e}$-dimensional smooth manifold. Two ${\displaystyle m}$-dimensional submanifolds ${\displaystyle M,M'}$ of ${\displaystyle E}$ are said to have the same ${\displaystyle k}$-th order Jet ${\displaystyle [M]_{p}^{k}}$ at ${\displaystyle p\in M\cap M'\subset E}$ if they are tangent up to order ${\displaystyle k}$. (To be tangent up to order ${\displaystyle k}$ means that if one locally describes the submanifolds as images of sections, then the derivatives of those sections agree up to order ${\displaystyle k}$.)

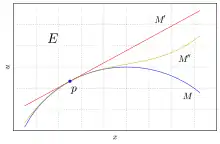${\displaystyle M}$ and ${\displaystyle M'}$ have the same 1-jet while ${\displaystyle M}$ and ${\displaystyle M''}$ have the same 3-jet.

One can show that being tangent up to order ${\displaystyle k}$ is a coordinate-invariant notion and an equivalence relation (see Saunders (1989) harvtxt error: no target: CITEREFSaunders1989 (help) for instance). Therefore a jet is an equivalence class. We can use jets to define jet spaces.

The Jet Space ${\displaystyle J^{k}(E,m)}$ is defined as the set of all jets of order ${\displaystyle k}$ of ${\displaystyle m}$-dimensional submanifolds in ${\displaystyle E}$ at all points of ${\displaystyle E}$, i.e. ${\displaystyle J^{k}(E,m):=\{[M]_{p}^{k}~|~M\ni p,~{\text{dim}}(M)=m,~p\in E\}}$

One can show that Jet Spaces are naturally endowed with the structure of a smooth manifold (see Saunders (1989) harvtxt error: no target: CITEREFSaunders1989 (help) again).

Remark regarding the relationship of Jet Spaces and Jet Bundles.

Instead of considering jets of submanifolds as above, it often suffices to define jets of sections of a fibered manifold ${\displaystyle \pi :E\rightarrow M}$. In this case one can describe those submanifolds that are horizontal to the projection ${\displaystyle \pi }$ as images of sections ${\displaystyle s}$ of the fibered manifold. A jet of sections is then an equivalence class of sections that are tangent up to order ${\displaystyle k}$ at some point ${\displaystyle p\in M}$. This gives rise to the definition of a Jet Bundle which is a slightly less general construction than a Jet Space. For more information, have a look at the Wikipedia page on Jet bundles.

Differential equations

A differential equation is a submanifold of a Jet Space, ${\displaystyle {\mathcal {E}}\subset J^{k}(E,m)}$.

If one defines solutions as below, then this geometric definition of PDEs in local coordinates gives rise to expressions that are usually used to define PDEs and their solutions in mathematical analysis.

Prolongation

The ${\displaystyle k}$-jet prolongation of a submanifold ${\displaystyle M\subset E}$, is the embedding ${\displaystyle j^{k}(M):M\rightarrow J^{k}(E,m)}$ given by ${\displaystyle j^{k}(M)(p):=[M]_{p}^{k}.}$ Furthermore, say that ${\displaystyle M^{k}:={\text{im}}(j^{k}(M))}$ is a prolongation of the submanifold ${\displaystyle M}$.

Furthermore, one can define prolongations of equations, i.e. of submanifolds of Jet spaces. To this end, consider a differential equation ${\displaystyle {\mathcal {E}}\subset J^{l}(E,m)}$. One would like the ${\displaystyle k}$-th prolongation of an equation of order ${\displaystyle l}$ to be an equation of order ${\displaystyle k+l}$, i.e. a submanifold of the jet space ${\displaystyle J^{k+l}(E,m)}$. To achieve this, one first constructs the jet space ${\displaystyle J^{k}({\mathcal {E}},m)}$ over ${\displaystyle m}$-dimensional submanifolds of ${\displaystyle {\mathcal {E}}}$. As ${\displaystyle {\mathcal {E}}}$ is embedded in ${\displaystyle J^{l}(E,m)}$, one can always naturally embed ${\displaystyle J^{k}({\mathcal {E}},m)}$ into ${\displaystyle J^{k}(J^{l}(E,m),m)}$. But since the latter is the space of repeated jets of submanifolds of ${\displaystyle E}$, one can also always embed ${\displaystyle J^{k+l}(E,m)}$ into ${\displaystyle J^{k}(J^{l}(E,m),m)}$. As a result, when considering both ${\displaystyle J^{k+l}(E,m)}$ and ${\displaystyle J^{k}({\mathcal {E}},m)}$ as subspaces of ${\displaystyle J^{k}(J^{l}(E,m),m)}$, their intersection is well-defined. This is used for the definition of the prolongation of ${\displaystyle {\mathcal {E}}}$.

The ${\displaystyle k}$-th prolongation of a differential equation ${\displaystyle {\mathcal {E}}\subset J^{l}(E,m)}$ is defined as ${\displaystyle {\mathcal {E}}^{k}:=J^{k}({\mathcal {E}},m)\cap J^{k+l}(E,m)}$

Note however that such an intersection is not necessarily a manifold again (i.e. does not always exist in the category of smooth manifolds). One therefore usually requires ${\displaystyle {\mathcal {E}}}$ to be nice enough such that at least its first prolongation is indeed a submanifold of ${\displaystyle J^{k+1}(E,m)}$.

It can also be shown that this definition still makes sense, even when ${\displaystyle k}$ goes to infinity.

Cartan distribution

Note that below a distribution is not understood in the sense of generalized functions but is considered to be a subbundle of the tangent bundle as is usually done when considering distributions in differential geometry.

An ${\displaystyle R}$-plane at a point ${\displaystyle \theta \in J^{k}(E,m)}$ is defined to be a subspace of the tangent space ${\displaystyle T_{\theta }(J^{k}(E,m))}$ of the form ${\displaystyle T_{\theta }(M^{k})}$ for any submanifold ${\displaystyle M}$ of ${\displaystyle E}$ (whose prolongation contains the point ${\displaystyle \theta }$).

The span of all ${\displaystyle R}$-planes at a point ${\displaystyle \theta \in J^{k}(E,m)}$ is denoted by ${\displaystyle {\mathcal {C}}_{\theta }}$. The map ${\displaystyle {\mathcal {C}}:J^{k}(E,m)\rightarrow TJ^{k}(E,m),\qquad \theta \mapsto {\mathcal {C}}_{\theta }\subset T_{\theta }(J^{k}(E,m))}$ is called Cartan Distribution (on ${\displaystyle J^{k}(E,m)}$).

The Cartan distribution is important in the algebro-geometric approach to differential equations because it allows to define generalized solutions of differential equations in purely geometric terms.

A generalized solution of a differential equation ${\displaystyle {\mathcal {E}}\subset J^{k}(E,m)}$ is defined to be an ${\displaystyle m}$-dimensional submanifold ${\displaystyle S\subset {\mathcal {E}}}$ that fulfills ${\displaystyle T_{\theta }S\subset {\mathcal {C}}_{\theta }}$ for all ${\displaystyle \theta \in S}$.

One can also look at the Cartan Distribution of a submanifold of ${\displaystyle J^{k}(E,m)}$ without the need to consider it inside ${\displaystyle J^{k}(E,m)}$. To do so, one defines the restriction of the Distribution to a submanifold of ${\displaystyle J^{k}(E,m)}$ as follows.

If ${\displaystyle {\mathcal {E}}\subset J^{k}(E,m)}$, then its Cartan Distribution is defined by ${\displaystyle {\mathcal {C}}({\mathcal {E}}):=\{{\mathcal {C}}_{\theta }\cap T_{\theta }({\mathcal {E}})~|~\theta \in {\mathcal {E}}\}}$

In this sense, the pair ${\displaystyle ({\mathcal {E}},{\mathcal {C}}({\mathcal {E}}))}$ encodes the information about the (generalized) solutions of the differential equation ${\displaystyle {\mathcal {E}}}$.

Definition of a diffiety

In Algebraic Geometry the main objects of study are varieties which include all algebraic consequences of a system of algebraic equations. For example, if one considers the zero locus of a set of polynomials, then applying algebraic operations to this set (like adding those polynomials to each other or multiplying them with any other polynomial) will give rise to the same zero locus, i.e. one can actually consider the zero locus of the algebraic ideal of the initial set of polynomials.

Now in the case of differential equations, apart from applying algebraic operations, one additionally has the option to differentiate. Therefore, the differential analogue of a variety should be like a differential ideal and should include all differential consequences. The natural object that does include the differential consequences of an equation ${\displaystyle {\mathcal {E}}}$ is its infinite prolongation ${\displaystyle {\mathcal {E}}^{\infty }}$. In general, it can be infinite dimensional. Additionally, one would like to pay attention to the geometric structure of the Cartan distribution defined above. Therefore, the pair ${\displaystyle ({\mathcal {E}}^{\infty },{\mathcal {C}}({\mathcal {E}}^{\infty }))}$ is defined as an elementary differential variety, or, for short, as an elementary diffiety.

If ${\displaystyle {\mathcal {E}}}$ is a ${\displaystyle k}$-th order differential equation, its elementary diffiety is the pair ${\displaystyle ({\mathcal {E}}^{\infty },{\mathcal {C}}({\mathcal {E}}^{\infty }))}$.

Note that when considering a differential equation ${\displaystyle {\mathcal {E}}\subset J^{k}(E,m)}$, then one can show that the Cartan distribution ${\displaystyle {\mathcal {C}}({\mathcal {E}}^{\infty })}$ is exactly ${\displaystyle m}$-dimensional unlike in the case of finitely many prolongations.

Elementary diffieties are geometric objects that play the same role in the theory of partial differential equations as affine algebraic varieties do in the theory of algebraic equations. Just like varieties or schemes are composed of irreducible affine varieties or affine schemes, one can also define a (non-elementary) diffiety as an object that locally looks like an elementary diffiety.

Suppose that ${\displaystyle {\mathcal {O}}}$ is a generally infinite dimensional manifold equipped with a smooth function algebra ${\displaystyle {\mathcal {F}}({\mathcal {O}})}$ and a finite dimensional distribution ${\displaystyle {\mathcal {C}}({\mathcal {O}})}$. A diffiety is a triple ${\displaystyle ({\mathcal {O}},{\mathcal {F}}({\mathcal {O}}),{\mathcal {C}}({\mathcal {O}}))}$ that is locally of the form ${\displaystyle ({\mathcal {E}}^{\infty },C^{\infty }({\mathcal {E}}^{\infty }),{\mathcal {C}}({\mathcal {E}}^{\infty }))}$ where ${\displaystyle {\mathcal {E}}}$ is a differential equation, ${\displaystyle C^{\infty }({\mathcal {E}}^{\infty })}$ denotes the class of infinitely differentiable functions on ${\displaystyle {\mathcal {E}}^{\infty }}$ and locally means a suitable localization with respect to the Zariski topology corresponding to the algebra ${\displaystyle {\mathcal {F}}({\mathcal {O}})}$.

Maps that are said to preserve the Cartan distribution are smooth maps ${\displaystyle \Phi$ :{\mathcal {O}}\rightarrow {\mathcal {O}}'} which are such that the pushforward ${\displaystyle d_{\theta }\Phi }$ at ${\displaystyle \theta \in {\mathcal {O}}}$ acts as follows:

${\displaystyle d_{\theta }\Phi (v\in {\mathcal {C}}_{\theta })\in {\mathcal {C}}_{\Phi (\theta )}}$

Diffieties together with maps that preserve the Cartan distribution are the objects and Morphisms of the Category of differential equations defined by Vinogradov. A thorough introduction to the topic is given in Vinogradov (2001) harvtxt error: no target: CITEREFVinogradov2001 (help).

Applications

Vinogradov sequence

The Vinogradov ${\displaystyle {\mathcal {C}}}$-spectral sequence (or, for short, Vinogradov sequence) is a spectral sequence related to the Cartan distribution ${\displaystyle {\mathcal {C}}}$ which Vinogradov invented (see Vinogradov (1978) harvtxt error: no target: CITEREFVinogradov1978 (help)) to calculate certain properties of the formal solution space of a differential equation. One may use diffieties to formulate it.

Assume that ${\displaystyle ({\mathcal {O}},{\mathcal {F}}({\mathcal {O}}),{\mathcal {C}}({\mathcal {O}}))}$ is a diffiety. Now define

${\displaystyle \Omega ({\mathcal {O}}):=\sum _{i\geq 0}\Omega ^{i}({\mathcal {O}})}$

to be the algebra of differential forms over ${\displaystyle {\mathcal {O}}}$. Consider the corresponding de Rham complex:

${\displaystyle C^{\infty }({\mathcal {O}})~{\color {Gray}\longrightarrow }~\Omega ^{1}({\mathcal {O}})~{\color {Gray}\longrightarrow }~\Omega ^{2}({\mathcal {O}})~{\color {Gray}\longrightarrow }~\cdots }$

Its cohomology groups ${\displaystyle H^{i}({\mathcal {O}}):={\text{ker}}({\text{d}}_{i})/{\text{im}}({\text{d}}_{i-1})}$ contain some structural information about the PDE. However, due to the Poincaré Lemma, they all vanish locally. In order to extract much more and even local information, one thus needs to take the Cartan distribution into account. This is what the Vinogradov sequence will facilitate. To this end, let

${\displaystyle {\mathcal {C}}\Omega ({\mathcal {O}})=\sum _{i\geq 0}{\mathcal {C}}\Omega ^{i}({\mathcal {O}})}$

be the submodule of differential forms ${\displaystyle \Omega ({\mathcal {O}})}$ over ${\displaystyle {\mathcal {O}}}$ whose restriction to the distribution vanishes. This means

${\displaystyle {\mathcal {C}}\Omega ^{p}({\mathcal {O}})\ni w{\text{ iff }}w(X_{1},\cdots ,X_{p})=0~\forall ~X_{1},\cdots ,X_{p}\in {\mathcal {C}}({\mathcal {O}}).}$

It is actually a so-called differential ideal since it is stable w.r.t. to the de Rham differential, i.e. ${\displaystyle {\text{d}}({\mathcal {C}}\Omega ^{i}({\mathcal {O}}))\subset {\mathcal {C}}\Omega ^{i+1}({\mathcal {O}})}$.

Now let ${\displaystyle {\mathcal {C}}^{k}\Omega ({\mathcal {O}})}$ be its ${\displaystyle k}$-th power, i.e. the linear subspace of ${\displaystyle {\mathcal {C}}\Omega }$ generated by ${\displaystyle w_{1}\wedge \cdots \wedge w_{k},~w_{i}\in {\mathcal {C}}\Omega }$. Then one obtains a filtration

${\displaystyle \Omega ({\mathcal {O}})\supset {\mathcal {C}}\Omega ({\mathcal {O}})\supset {\mathcal {C}}^{2}\Omega ({\mathcal {O}})\supset \cdots }$

and since all ideals ${\displaystyle {\mathcal {C}}^{k}\Omega }$ are stable, this filtration completely determines a spectral sequence. (For more information on how spectral sequences work, see spectral sequence.) We denote this sequence by

${\displaystyle {\mathcal {C}}E({\mathcal {O}})=\{E_{r}^{p,q},{\text{d}}_{r}^{p,q}\}\qquad {\text{where}}\qquad E_{0}^{p,q}:={\frac {{\mathcal {C}}^{p}\Omega ^{p+q}({\mathcal {O}})}{{\mathcal {C}}^{p+1}\Omega ^{p+q}({\mathcal {O}})}},\qquad {\text{and}}\qquad E_{r+1}^{p,q}:=H(E_{r}^{p,q},d_{r}^{p,q})}$

The filtration above is finite in each degree, that means

${\displaystyle \Omega ^{k}({\mathcal {O}})\supset {\mathcal {C}}^{1}\Omega ^{k}({\mathcal {O}})\supset \cdots \supset {\mathcal {C}}^{k+1}\Omega ^{k}({\mathcal {O}})=0}$

If the filtration is finite in this sense, then the spectral sequence converges to the de Rham cohomology ${\displaystyle H({\mathcal {O}})}$ (of the diffiety). Therefore, one can now analyse the terms of the spectral sequence order by order. This is done for example in chapter 5 of Krasilshchik (1999) harvtxt error: no target: CITEREFKrasilshchik1999 (help). Here will only be summarized which information is contained in the Vinogradov sequence.

1. ${\displaystyle E_{1}^{0,n}}$ corresponds to action functionals constrained by the PDE ${\displaystyle {\mathcal {E}}}$ and for ${\displaystyle {\mathcal {L}}\in E_{1}^{0,n}}$, the corresponding Euler-Lagrange equation is ${\displaystyle {\text{d}}_{1}^{0,n}{\mathcal {L}}=0}$.
2. ${\displaystyle E_{1}^{0,n-1}}$ corresponds to conservation laws for solutions of ${\displaystyle {\mathcal {E}}}$.
3. ${\displaystyle E_{2}}$ is interpreted as characteristic classes of bordisms of solutions of ${\displaystyle {\mathcal {E}}}$.
4. There are still many terms awaiting an interpretation.

Remark regarding the variational bicomplex.

If one considers a jet bundle instead of a jet space, then instead of the ${\displaystyle {\mathcal {C}}}$-spectral sequence, one obtains the slightly less general variational bicomplex. (Any bicomplex determines two spectral sequences. One of the two spectral sequences determined by the variational bicomplex is exactly the Vinogradov ${\displaystyle {\mathcal {C}}}$-spectral sequence. However, the variational bicomplex was also developed independently from the Vinogradov sequence.) Similarly to the terms of the spectral sequence, many of its terms can be given a physical interpretation if one considers the diffiety (that is, roughly, the solution space of a PDE) of a classical field theory. For example, one obtains cohomology classes corresponding to action functionals, conserved currents, gauge charges and other important notions in one unifiedly organized scheme. Since the Wikipedia article on the variational bicomplex is currently quite short, the reader is instead referred to the article of the nLab for more information.

Secondary Calculus

Vinogradov developed a theory, which is known as secondary calculus (see Vinogradov (1984b) harvtxt error: no target: CITEREFVinogradov1984b (help), Vinogradov (1998) harvtxt error: no target: CITEREFVinogradov1998 (help), Vinogradov (2001) harvtxt error: no target: CITEREFVinogradov2001 (help)), formalizing in cohomological terms the idea of a differential calculus on the space of solutions of a given system of PDEs, or, which is roughly the same, the space of integral manifolds of a given diffiety. In other words, secondary calculus provides substitutes for vector fields, differential forms, differential operators, etc., on a (generically) very singular space where these objects cannot be defined in the usual (smooth) way. (This summary was taken from the introduction of Vitagliano (2014) harvtxt error: no target: CITEREFVitagliano2014 (help).)

In Vitagliano (2009) harvtxt error: no target: CITEREFVitagliano2009 (help) is analyzed the relationship between Secondary Calculus and the Covariant Phase Space (which is the solution space of the Euler-Lagrange equations associated to a Lagrangian field theory).

See also

• Secondary calculus and cohomological physics
• Partial differential equations on Jet bundles
• Differential ideal
• Differential calculus over commutative algebras

Another way of generalizing ideas from algebraic geometry is differential algebraic geometry.

References

• Vinogradov, A. M. (1978), "A spectral sequence associated with a nonlinear differential equation and algebro-geometric foundations of Lagrangian field theory with constraints", Soviet Math. Dokl., 19: 144–148
• Vinogradov, A. M. (1984a), "Local symmetries and conservation laws", Acta Applicandae Mathematicae, 2 (1): 21–78, doi:10.1007/BF01405491, MR 0736872
• Vinogradov, A. M. (1984b), "The C-spectral sequence, Lagrangian formalism and conservation laws I, II", J. Math. Anal. Appl., 100: 1–129, doi:10.1016/0022-247X(84)90071-4
• Saunders, D. J. (1989). The Geometry of Jet Bundles. London Mathematical Society Lecture Note Series. Cambridge University Press.
• Vinogradov, A. M. (1998), "Introduction to secondary calculus", in M. Henneaux; I. S. Krasil’shchik; A. M. Vinogradov (eds.), Secondary Calculus and Cohomological Physics, Contemporary Mathematics, 219, American Mathematical Society, pp. 241–272, ISBN 978-0-8218-0828-3
• Krasilshchik, I. S.; Vinogradov, A. M.; Bocharov, A. V.; Chetverikov, V. N.; Duzhin, S. V.; Khor’kova, N. G.; Samokhin, A. V.; Torkhov, Y. N.; Verbovetsky, A. M. (1999). Symmetries and Conservation Laws for Differential Equations of Mathematical Physics. Translations of Mathematical Monographs. American Mathematical Society.
• Vinogradov, Aleksandr Mikhaĭlovich (2001), Cohomological analysis of partial differential equations and secondary calculus, AMS Bookstore, ISBN 978-0-8218-2922-6
• Vitagliano, Luca (2009), "Secondary Calculus and the Covariant Phase Space", Journal of Geometry and Physics, 59 (4): 426–447, arXiv:0809.4164, Bibcode:2009JGP....59..426V, doi:10.1016/j.geomphys.2008.12.001
• Vitagliano, Luca (2014), "On the Strong Homotopy Lie-Rinehart Algebra of a Foliation", Communications in Contemporary Mathematics, 16 (6): 1450007, arXiv:1204.2467, doi:10.1142/S0219199714500072

External links

• The Diffiety Institute (frozen since 2010 but contains useful, related material)
• The Levi-Civita Institute (successor of above site with current information on diffiety schools)
• Geometry of Differential Equations