Conway's 99-graph problem

In graph theory, Conway's 99-graph problem is an unsolved problem asking whether there exists an undirected graph with 99 vertices, in which each two adjacent vertices have exactly one common neighbor, and in which each two non-adjacent vertices have exactly two common neighbors. Equivalently, every edge should be part of a unique triangle and every non-adjacent pair should be one of the two diagonals of a unique 4-cycle. John Horton Conway offered a $1000 prize for its solution.[1]

Unsolved problem in mathematics:
Does there exist a strongly regular graph with parameters (99,14,1,2)?
(more unsolved problems in mathematics)
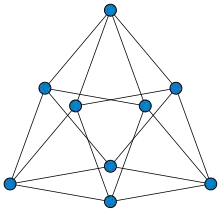
A 9-vertex graph in which every edge belongs to a unique triangle and every non-edge is the diagonal of a unique quadrilateral. The 99-graph problem asks for a 99-vertex graph with the same property.

Properties

If such a graph exists, it would necessarily be a locally linear graph and a strongly regular graph with parameters (99,14,1,2). The first, third, and fourth parameters encode the statement of the problem: the graph should have 99 vertices, every pair of adjacent vertices should have 1 common neighbor, and every pair of non-adjacent vertices should have 2 common neighbors. The second parameter means that the graph is a regular graph with 14 edges per vertex.[2]

If this graph exists, it does not have any symmetries of order 11, which implies that its symmetries cannot take every vertex to every other vertex.[3] Additional restrictions on its possible groups of symmetries are known.[4]

History

The possibility of a graph with these parameters was already suggested in 1969 by Norman L. Biggs,[5] and its existence noted as an open problem by others before Conway.[3][6][7][8] Conway himself had worked on the problem as early as 1975,[6] but offered the prize in 2014 as part of a set of problems posed in the DIMACS Conference on Challenges of Identifying Integer Sequences. Other problems in the set include the thrackle conjecture, the minimum spacing of Danzer sets, and the question of who wins after the move 16 in the game sylver coinage.[1]

More generally, there are only five possible combinations of parameters for which a strongly regular graph could exist with each edge in a unique triangle and each non-edge forming the diagonal of a unique quadrilateral. It is only known that graphs exist with two of these five combinations. These two graphs are the nine-vertex Paley graph (the graph of the 3-3 duoprism) with parameters (9,4,1,2) and the Berlekamp–van Lint–Seidel graph with parameters (243,22,1,2). The parameters for which graphs are unknown are: (99,14,1,2), (6273,112,1,2) and (494019,994,1,2). The 99-graph problem describes the smallest of these combinations of parameters for which the existence of a graph is unknown.[4]

References
  1. Conway, John H., Five $1,000 Problems (Update 2017) (PDF), On-Line Encyclopedia of Integer Sequences, retrieved 2019-02-12. See also OEIS sequence A248380.
  2. Zehavi, Sa'ar; David de Olivera, Ivo Fagundes (2017), Not Conway's 99-graph problem, arXiv:1707.08047
  3. Wilbrink, H. A. (August 1984), "On the (99,14,1,2) strongly regular graph", in de Doelder, P. J.; de Graaf, de, J.; van Lint, J. H. (eds.), Papers dedicated to J. J. Seidel (PDF), EUT Report, 84-WSK-03, Eindhoven University of Technology, pp. 342–355
  4. Makhnev, A. A.; Minakova, I. M. (January 2004), "On automorphisms of strongly regular graphs with parameters , ", Discrete Mathematics and Applications, 14 (2), doi:10.1515/156939204872374, MR 2069991, S2CID 118034273
  5. Biggs, Norman (1971), Finite Groups of Automorphisms: Course Given at the University of Southampton, October–December 1969, London Mathematical Society Lecture Note Series, 6, London and New York: Cambridge University Press, p. 111, ISBN 9780521082150, MR 0327563
  6. Guy, Richard K. (1975), "Problems", in Kelly, L. M. (ed.), Proceedings of a Conference held at Michigan State University, East Lansing, Mich., June 17–19, 1974, Lecture Notes in Mathematics, 490, Berlin and New York: Springer-Verlag, pp. 233–244, doi:10.1007/BFb0081147, MR 0388240. See problem 7 (J. J. Seidel), pp. 237–238.
  7. Brouwer, A. E.; Neumaier, A. (1988), "A remark on partial linear spaces of girth 5 with an application to strongly regular graphs", Combinatorica, 8 (1): 57–61, doi:10.1007/BF02122552, MR 0951993, S2CID 206812356
  8. Cameron, Peter J. (1994), Combinatorics: topics, techniques, algorithms, Cambridge: Cambridge University Press, p. 331, ISBN 0-521-45133-7, MR 1311922
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.