Clique percolation method

The clique percolation method[1] is a popular approach for analyzing the overlapping community structure of networks. The term network community (also called a module, cluster or cohesive group) has no widely accepted unique definition and it is usually defined as a group of nodes that are more densely connected to each other than to other nodes in the network. There are numerous alternative methods for detecting communities in networks,[2] for example, the Girvan–Newman algorithm, hierarchical clustering and modularity maximization.

Definitions

Clique Percolation Method (CPM)

The clique percolation method builds up the communities from k-cliques, which correspond to complete (fully connected) sub-graphs of k nodes. (E.g., a k-clique at k = 3 is equivalent to a triangle). Two k-cliques are considered adjacent if they share k − 1 nodes. A community is defined as the maximal union of k-cliques that can be reached from each other through a series of adjacent k-cliques. Such communities can be best interpreted with the help of a k-clique template (an object isomorphic to a complete graph of k nodes). Such a template can be placed onto any k-clique in the graph, and rolled to an adjacent k-clique by relocating one of its nodes and keeping its other k − 1 nodes fixed. Thus, the k-clique communities of a network are all those sub-graphs that can be fully explored by rolling a k-clique template in them, but cannot be left by this template.

This definition allows overlaps between the communities in a natural way, as illustrated in Fig.1, showing four k-clique communities at k = 4. The communities are color-coded and the overlap between them is emphasized in red. The definition above is also local: if a certain sub-graph fulfills the criteria to be considered as a community, then it will remain a community independent of what happens to another part of the network far away. In contrast, when searching for the communities by optimizing with respect to a global quantity, a change far away in the network can reshape the communities in the unperturbed regions as well. Furthermore, it has been shown that global methods can suffer from a resolution limit problem,[3] where the size of the smallest community that can be extracted is dependent on the system size. A local community definition such as here circumvents this problem automatically.

Since even small networks can contain a vast number of k-cliques, the implementation of this approach is based on locating all maximal cliques rather than the individual k-cliques.[1] This inevitably requires finding the graph's maximum clique, which is an NP-hard problem. (We emphasize to the reader that finding a maximum clique is much harder than finding a single maximal clique.) This means that although networks with few million nodes have already been analyzed successfully with this approach,[4] the worst case runtime complexity is exponential in the number of nodes.

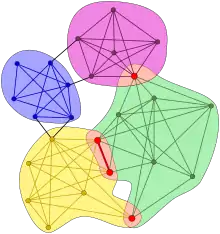  • Fig.1. Illustration of the k-clique communities at k = 4.

Directed Clique Percolation Method (CPMd)

On a network with directed links a directed k-clique is a complete subgraph with k nodes fulfilling the following condition. The k nodes can be ordered such that between an arbitrary pair of them there exists a directed link pointing from the node with the higher rank towards the node with the lower rank. The directed Clique Percolation Method defines directed network communities as the percolation clusters of directed k-cliques.

Weighted Clique Percolation Method (CPMw)

On a network with weighted links a weighted k-clique is a complete subgraph with k nodes such that the geometric mean of the k (k - 1) / 2 link weights within the k-clique is greater than a selected threshold value, I. The weighted Clique Percolation Method defines weighted network communities as the percolation clusters of weighted k-cliques. Note that the geometric mean of link weights within a subgraph is called the intensity of that subgraph.[5]

Clique Graph Generalizations

Clique percolation methods may be generalized by recording different amounts of overlap between the various k-cliques. This then defines a new type of graph, a clique graph,[6] where each k-clique in the original graph is represented by a vertex in the new clique graph. The edges in the clique graph are used to record the strength of the overlap of cliques in the original graph. One may then apply any community detection method to this clique graph to identify the clusters in the original graph through the k-clique structure.

For instance in a simple graph, we can define the overlap between two k-cliques to be the number of vertices common to both k-cliques. The Clique Percolation Method is then equivalent to thresholding this clique graph, dropping all edges of weight less than (k-1), with the remaining connected components forming the communities of cliques found in CPM. For k=2 the cliques are the edges of the original graph and the clique graph in this case is the line graph of the original network.

In practice, using the number of common vertices as a measure of the strength of clique overlap may give poor results as large cliques in the original graph, those with many more than k vertices, will dominate the clique graph. The problem arises because if a vertex is in n different k-cliques it will contribute to n(n-1)/2 edges in such a clique graph. A simple solution is to let each vertex common to two overlapping kcliques to contribute a weight equal to 1/n when measuring the overlap strength of the two k-cliques.

In general the clique graph viewpoint is a useful way of finding generalizations of standard clique-percolation methods to get around any problems encountered. It even shows how to describe extensions of these methods based on other motifs, subgraphs other than k-cliques. In this case a clique graph is best thought of a particular example of a hypergraph.

Percolation transition in the CPM

The Erdős–Rényi model shows a series of interesting transitions when the probability p of two nodes being connected is increased. For each k one can find a certain threshold probability pc above which the k-cliques organize into a giant community.[7][8][9](The size of the giant community is comparable to the system size, in other words the giant community occupies a finite part of the system even in the thermodynamic limit.) This transition is analogous to the percolation transition in statistical physics. A similar phenomenon can be observed in many real networks as well: if k is large, only the most densely linked parts are accepted as communities, thus, they usually remain small and dispersed. When k is lowered, both the number and the size of the communities start to grow. However, in most cases a critical k value can be reached, below which a giant community emerges, smearing out the details of the community structure by merging (and making invisible) many smaller communities.

Applications

The clique percolation method had been used to detect communities from the studies of cancer metastasis[10][11] through various social networks[4][12][13][14][15] to document clustering[16] and economical networks.[17]

Algorithms and software

There are a number of implementations of clique percolation. The clique percolation method was first implemented and popularized by CFinder (freeware for non-commercial use) software for detecting and visualizing overlapping communities in networks. The program enables customizable visualization and allows easy strolling over the found communities. The package contains a command line version of the program as well, which is suitable for scripting.

A faster implementation (available under the GPL) has been implemented by another group.[18] Another example, which is also very fast in certain contexts, is the SCP algorithm.[19]

Parallel algorithms

A parallel version of the clique percolation method was designed and developed by S. Mainardi et al..[20] By exploiting today's multi-core/multi-processor computing architectures, the method enables the extraction of k-clique communities from very large networks such as the Internet.[21] The authors released the source code of the method under the GPL and made it freely available for the community.

See also
  • Social network
  • Community structure
  • Survey Article Communities in Networks
  • Fortunato, Santo (2010). "Community detection in graphs". Physics Reports. 486 (3–5): 75–174. arXiv:0906.0612. Bibcode:2010PhR...486...75F. doi:10.1016/j.physrep.2009.11.002.
  • Bibliography of community structure links

References
  1. Palla, Gergely (2005). "Uncovering the overlapping community structure of complex networks in nature and society". Nature. 435 (7043): 814–818. arXiv:physics/0506133. Bibcode:2005Natur.435..814P. doi:10.1038/nature03607. PMID 15944704.
  2. Fortunato, Santo (2010). "Community detection in graphs". Physics Reports. 486 (3–5): 75–174. arXiv:0906.0612. Bibcode:2010PhR...486...75F. doi:10.1016/j.physrep.2009.11.002.
  3. Fortunato, S. (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences. 104 (1): 36–41. arXiv:physics/0607100. Bibcode:2007PNAS..104...36F. doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818.
  4. Palla, Gergely (2007). "Quantifying social group evolution". Nature. 446 (7136): 664–667. arXiv:0704.0744. Bibcode:2007Natur.446..664P. doi:10.1038/nature05670. PMID 17410175.
  5. Onnela, Jukka-Pekka; Saramäki, Jari; Kertész, János; Kaski, Kimmo (2005). "Intensity and coherence of motifs in weighted complex networks". Physical Review E. 71 (6): 065103. arXiv:cond-mat/0408629. Bibcode:2005PhRvE..71f5103O. doi:10.1103/PhysRevE.71.065103. PMID 16089800.
  6. Evans, T S (2010). "Clique graphs and overlapping communities". Journal of Statistical Mechanics: Theory and Experiment. 2010 (12): P12037. arXiv:1009.0638. Bibcode:2010JSMTE..12..037E. doi:10.1088/1742-5468/2010/12/P12037.
  7. Derényi, Imre; Palla, Gergely; Vicsek, Tamás (2005). "Clique Percolation in Random Networks". Physical Review Letters. 94 (16): 160202. arXiv:cond-mat/0504551. Bibcode:2005PhRvL..94p0202D. doi:10.1103/PhysRevLett.94.160202. PMID 15904198.
  8. Palla, Gergely; Derényi, Imre; Vicsek, Tamás (2006). "The Critical Point of k-Clique Percolation in the Erdős–Rényi Graph". Journal of Statistical Physics. 128 (1–2): 219–227. arXiv:cond-mat/0610298. Bibcode:2007JSP...128..219P. doi:10.1007/s10955-006-9184-x.
  9. Li, Ming; Deng, Youjin; Wang, Bing-Hong (2015). "Clique percolation in random graphs". Physical Review E. 92 (4): 042116. arXiv:1508.01878. Bibcode:2015PhRvE..92d2116L. doi:10.1103/PhysRevE.92.042116. PMID 26565177.
  10. Jonsson, P. F. (2006). "Global topological features of cancer proteins in the human interactome". Bioinformatics. 22 (18): 2291–2297. doi:10.1093/bioinformatics/btl390. PMC 1865486. PMID 16844706.
  11. Jonsson, PF; Cavanna, T; Zicha, D; Bates, PA (2006). "Cluster analysis of networks generated through homology: automatic identification of important protein communities involved in cancer metastasis". BMC Bioinformatics. 7: 2. doi:10.1186/1471-2105-7-2. PMC 1363365. PMID 16398927.
  12. González, Marta C.; Lind, Pedro G.; Herrmann, Hans J. (2006). "System of Mobile Agents to Model Social Networks". Physical Review Letters. 96 (8): 088702. arXiv:physics/0602091. Bibcode:2006PhRvL..96h8702G. doi:10.1103/PhysRevLett.96.088702. PMID 16606237.
  13. Kumpula, Jussi M.; Onnela, Jukka-Pekka; Saramäki, Jari; Kaski, Kimmo; Kertész, János (2007). "Emergence of Communities in Weighted Networks". Physical Review Letters. 99 (22): 228701. arXiv:0708.0925. Bibcode:2007PhRvL..99v8701K. doi:10.1103/PhysRevLett.99.228701. PMID 18233339.
  14. Toivonen, Riitta; Onnela, Jukka-Pekka; Saramäki, Jari; Hyvönen, Jörkki; Kaski, Kimmo (2006). "A model for social networks". Physica A: Statistical Mechanics and Its Applications. 371 (2): 851–860. arXiv:physics/0601114. Bibcode:2006PhyA..371..851T. doi:10.1016/j.physa.2006.03.050.
  15. González, M.C.; Herrmann, H.J.; Kertész, J.; Vicsek, T. (2007). "Community structure and ethnic preferences in school friendship networks". Physica A: Statistical Mechanics and Its Applications. 379 (1): 307–316. arXiv:physics/0611268. Bibcode:2007PhyA..379..307G. doi:10.1016/j.physa.2007.01.002.
  16. Gao, Wei; Wong, Kam-Fai (2006). Natural Document Clustering by Clique Percolation in Random Graphs. Lecture Notes in Computer Science. 4182. pp. 119–131. doi:10.1007/11880592_10. ISBN 978-3-540-45780-0.
  17. Heimo, Tapio; Saramäki, Jari; Onnela, Jukka-Pekka; Kaski, Kimmo (2007). "Spectral and network methods in the analysis of correlation matrices of stock returns". Physica A: Statistical Mechanics and Its Applications. 383 (1): 147–151. arXiv:physics/0703061. Bibcode:2007PhyA..383..147H. doi:10.1016/j.physa.2007.04.124.
  18. Reid, F.; McDaid, A.; Hurley, N.; Vicsek, Tamas (2012). "Percolation Computation in Complex Networks". 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. pp. 274–281. arXiv:1205.0038. doi:10.1109/ASONAM.2012.54. ISBN 978-1-4673-2497-7.
  19. Kumpula, Jussi M.; Kivelä, Mikko; Kaski, Kimmo; Saramäki, Jari (2008). "Sequential algorithm for fast clique percolation". Physical Review E. 78 (2): 026109. arXiv:0805.1449. Bibcode:2008PhRvE..78b6109K. doi:10.1103/PhysRevE.78.026109. PMID 18850899.
  20. Gregori, Enrico; Lenzini, Luciano; Mainardi, Simone (2013). "Parallel k-Clique Community Detection on Large-Scale Networks" (PDF). IEEE Transactions on Parallel and Distributed Systems. 24 (8): 1651–1660. doi:10.1109/TPDS.2012.229.
  21. Gregori, Enrico; Lenzini, Luciano; Orsini, Chiara (2011). "K-clique Communities in the Internet AS-level Topology Graph". 2011 31st International Conference on Distributed Computing Systems Workshops. pp. 134–139. doi:10.1109/ICDCSW.2011.17. ISBN 978-1-4577-0384-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.