Bevan point
The Bevan point, named after Benjamin Bevan, is a triangle center. It is defined as center of the Bevan circle, that is the circle through the centers of the three excircles of a triangle.
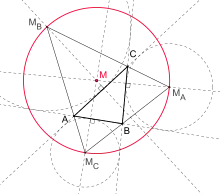
Bevan point M and Bevan Circle (red) of triangle ABC
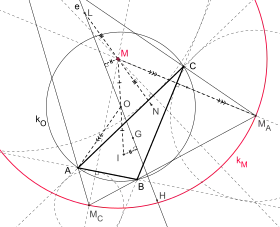
Bevan point M, Bevan circle kM, orthocenter H, gravity center G, circumcenter O, incenter I, Euler line e, circumcircle kO
The Bevan point M of triangle ABC has the same distance from its Euler line e as its incenter I and the circumcenter O is the midpoint of the line segment MI. The length of MI is given by
where R denotes the radius of the circumcircle and a, b and c the sides of the triangle ABC. The Bevan is point is also the midpoint of the line segment NL connecting the Nagel point N and the Longchamps point L. The radius of the Bevan circle is 2R, that is twice the radius of the circumcircle.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.