Bayesian optimization
Bayesian optimization is a sequential design strategy for global optimization of black-box functions[1] that does not assume any functional forms. It is usually employed to optimize expensive-to-evaluate functions.
History
The term is generally attributed to Jonas Mockus and is coined in his work from a series of publications on global optimization in the 1970s and 1980s.[2][3][4]
Strategy
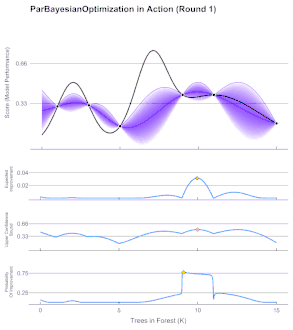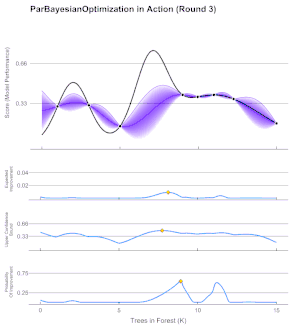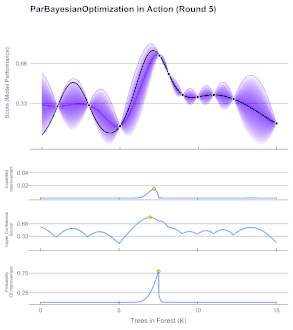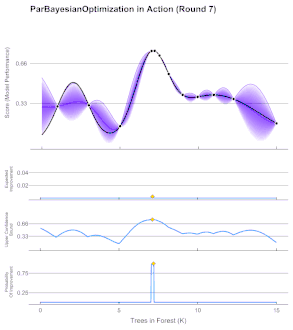
Bayesian optimization is typically used on problems of the form , where is a set of points whose membership can easily be evaluated. Bayesian optimization is particularly advantageous for problems where is difficult to evaluate, is a black box with some unknown structure, relies upon less than 20 dimensions, and where derivatives are not evaluated.[6]
Since the objective function is unknown, the Bayesian strategy is to treat it as a random function and place a prior over it. The prior captures beliefs about the behavior of the function. After gathering the function evaluations, which are treated as data, the prior is updated to form the posterior distribution over the objective function. The posterior distribution, in turn, is used to construct an acquisition function (often also referred to as infill sampling criteria) that determines the next query point.
There are several methods used to define the prior/posterior distribution over the objective function. The most common two methods use Gaussian Processes in a method called Kriging. Another less expensive method uses the Parzen-Tree Estimator to construct two distributions for 'high' and 'low' points, and then finds the location that maximizes the expected improvement.[7]
Standard Bayesian optimization relies upon each being easy to evaluate, and problems that deviate from this assumption are known as exotic Bayesian optimization problems. Optimization problems can become exotic if it is known that there is noise, the evaluations are being done in parallel, the quality of evaluations relies upon a tradeoff between difficulty and accuracy, the presence of random environmental conditions, or if the evaluation involves derivatives.[6]
Examples
Examples of acquisition functions include probability of improvement, expected improvement, Bayesian expected losses, upper confidence bounds (UCB), Thompson sampling and hybrids of these.[8] They all trade-off exploration and exploitation so as to minimize the number of function queries. As such, Bayesian optimization is well suited for functions that are expensive to evaluate.
Solution methods
The maximum of the acquisition function is typically found by resorting to discretization or by means of an auxiliary optimizer. Acquisition functions are typically well-behaved and are often maximized with implementations of Newton's Method such as Broyden–Fletcher–Goldfarb–Shanno algorithm or the Nelder-Mead method.
Applications
The approach has been applied to solve a wide range of problems,[9] including learning to rank,[10] computer graphics and visual design,[11][12] robotics,[13][14][15][16] sensor networks,[17][18] automatic algorithm configuration,[19][20] automatic machine learning toolboxes,[21][22][23] reinforcement learning, planning, visual attention, architecture configuration in deep learning, static program analysis, experimental particle physics,[24][25] chemistry, material design, and drug development.[6][26][27]
References
- Jonas Mockus (2012). Bayesian approach to global optimization: theory and applications. Kluwer Academic.
- Jonas Mockus: On Bayesian Methods for Seeking the Extremum. Optimization Techniques 1974: 400-404
- Jonas Mockus: On Bayesian Methods for Seeking the Extremum and their Application. IFIP Congress 1977: 195-200
- J. Mockus, Bayesian Approach to Global Optimization. Kluwer Academic Publishers, Dordrecht, 1989
- Wilson, Samuel (2019-11-22), ParBayesianOptimization R package, retrieved 2019-12-12
- Frazier, Peter I. (2018-07-08). "A Tutorial on Bayesian Optimization". arXiv:1807.02811 [stat.ML].
- J. S. Bergstra, R. Bardenet, Y. Bengio, B. Kégl: Algorithms for Hyper-Parameter Optimization. Advances in Neural Information Processing Systems: 2546–2554 (2011)
- Matthew W. Hoffman, Eric Brochu, Nando de Freitas: Portfolio Allocation for Bayesian Optimization. Uncertainty in Artificial Intelligence: 327–336 (2011)
- Eric Brochu, Vlad M. Cora, Nando de Freitas: A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. CoRR abs/1012.2599 (2010)
- Eric Brochu, Nando de Freitas, Abhijeet Ghosh: Active Preference Learning with Discrete Choice Data. Advances in Neural Information Processing Systems: 409-416 (2007)
- Eric Brochu, Tyson Brochu, Nando de Freitas: A Bayesian Interactive Optimization Approach to Procedural Animation Design. Symposium on Computer Animation 2010: 103–112
- Yuki Koyama, Issei Sato, Daisuke Sakamoto, Takeo Igarashi: Sequential Line Search for Efficient Visual Design Optimization by Crowds. ACM Transactions on Graphics, Volume 36, Issue 4, pp.48:1–48:11 (2017). DOI: https://doi.org/10.1145/3072959.3073598
- Daniel J. Lizotte, Tao Wang, Michael H. Bowling, Dale Schuurmans: Automatic Gait Optimization with Gaussian Process Regression. International Joint Conference on Artificial Intelligence: 944–949 (2007)
- Ruben Martinez-Cantin, Nando de Freitas, Eric Brochu, Jose Castellanos and Arnaud Doucet. A Bayesian exploration-exploitation approach for optimal online sensing and planning with a visually guided mobile robot. Autonomous Robots. Volume 27, Issue 2, pp 93–103 (2009)
- Scott Kuindersma, Roderic Grupen, and Andrew Barto. Variable Risk Control via Stochastic Optimization. International Journal of Robotics Research, volume 32, number 7, pp 806–825 (2013)
- Roberto Calandra, André Seyfarth, Jan Peters, and Marc P. Deisenroth Bayesian optimization for learning gaits under uncertainty. Ann. Math. Artif. Intell. Volume 76, Issue 1, pp 5-23 (2016) DOI:10.1007/s10472-015-9463-9
- Niranjan Srinivas, Andreas Krause, Sham M. Kakade, Matthias W. Seeger: Information-Theoretic Regret Bounds for Gaussian Process Optimization in the Bandit Setting. IEEE Transactions on Information Theory 58(5):3250–3265 (2012)
- Roman Garnett, Michael A. Osborne, Stephen J. Roberts: Bayesian optimization for sensor set selection. ACM/IEEE International Conference on Information Processing in Sensor Networks: 209–219 (2010)
- Frank Hutter, Holger Hoos, and Kevin Leyton-Brown (2011). Sequential model-based optimization for general algorithm configuration, Learning and Intelligent Optimization
- J. Snoek, H. Larochelle, R. P. Adams Practical Bayesian Optimization of Machine Learning Algorithms. Advances in Neural Information Processing Systems: 2951-2959 (2012)
- J. Bergstra, D. Yamins, D. D. Cox (2013). Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms. Proc. SciPy 2013.
- Chris Thornton, Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown: Auto-WEKA: combined selection and hyperparameter optimization of classification algorithms. KDD 2013: 847–855
- Jasper Snoek, Hugo Larochelle and Ryan Prescott Adams. Practical Bayesian Optimization of Machine Learning Algorithms. Advances in Neural Information Processing Systems, 2012
- Philip Ilten, Mike Williams, Yunjie Yang. Event generator tuning using Bayesian optimization. 2017 JINST 12 P04028. DOI: 10.1088/1748-0221/12/04/P04028
- Evaristo Cisbani et al. AI-optimized detector design for the future Electron-Ion Collider: the dual-radiator RICH case 2020 JINST 15 P05009. DOI: 10.1088/1748-0221/15/05/P05009
- Gomez-Bombarelli et al. Automatic Chemical Design using a Data-Driven Continuous Representation of Molecules. ACS Central Science, Volume 4, Issue 2, 268-276 (2018)
- Griffiths et al. Constrained Bayesian Optimization for Automatic Chemical Design using Variational Autoencoders Chemical Science: 11, 577-586 (2020)
External links
- GPyOpt, Python open-source library for Bayesian Optimization based on GPy.
- Bayesopt, an efficient implementation in C/C++ with support for Python, Matlab and Octave.
- Spearmint, a Python implementation focused on parallel and cluster computing.
- SMAC, a Java implementation of random-forest-based Bayesian optimization for general algorithm configuration.
- ParBayesianOptimization, A high performance, parallel implementation of Bayesian optimization with Gaussian processes in R.
- pybo, a Python implementation of modular Bayesian optimization.
- Bayesopt.m, a Matlab implementation of Bayesian optimization with or without constraints.
- MOE MOE is a Python/C++/CUDA implementation of Bayesian Global Optimization using Gaussian Processes.
- SigOpt SigOpt offers Bayesian Global Optimization as a SaaS service focused on enterprise use cases.
- Mind Foundry OPTaaS offers Bayesian Global Optimization via web-services with flexible parameter constraints.
- bayeso, a Python implementation of Bayesian optimization.
- BoTorch, a modular and modern PyTorch-based open-source library for Bayesian optimization research with support for GPyTorch.
- GPflowOpt, a TensorFlow-based open-source package for Bayesian optimization.