Activation function

In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard integrated circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the behavior of the linear perceptron in neural networks. However, only nonlinear activation functions allow such networks to compute nontrivial problems using only a small number of nodes, and such activation functions are called nonlinearities.[1]

Logistic activation function

Classification of activation functions

The most common activation functions can be divided in three categories: ridge functions, radial functions and fold functions.

Ridge activation functions

Ridge functions are multivariate functions acting on a linear combination of the input variables. Often used examples include:

• Linear activation: ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$,
• ReLU activation: ${\displaystyle \phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )}$,
• Heaviside activation: ${\displaystyle \phi (\mathbf {v} )=1_{a+\mathbf {v} '\mathbf {b} >0}}$,
• Logistic activation: ${\displaystyle \phi (\mathbf {v} )=(1+\exp(-a-\mathbf {v} '\mathbf {b} ))^{-1}}$.

In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell.[2] In its simplest form, this function is binary—that is, either the neuron is firing or not. The function looks like ${\displaystyle \phi (\mathbf {v} )=U(a+\mathbf {v} '\mathbf {b} )}$, where ${\displaystyle U}$ is the Heaviside step function.

A line of positive slope may be used to reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$.

As biological neurons cannot lower their firing rate below zero, rectified linear activation functions are used: ${\displaystyle \phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )}$. They introduce a non-linearity at zero that can be used for decision making.[3]

Rectified linear unit and Gaussian error linear unit activation functions

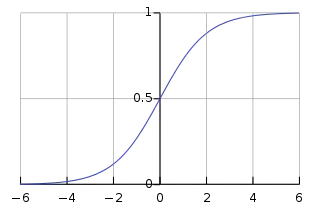
Neurons also cannot fire faster than a certain rate, motivating sigmoid activation functions whose domain is a finite interval.

Radial activation functions

A special class of activation functions known as radial basis functions (RBFs) are used in RBF networks, which are extremely efficient as universal function approximators. These activation functions can take many forms, but they are usually found as one of the following functions:

• Gaussian: ${\displaystyle \,\phi (\mathbf {v} )=\exp \left(-{\frac {\|\mathbf {v} -\mathbf {c} \|^{2}}{2\sigma ^{2}}}\right)}$
• Multiquadratics: ${\displaystyle \,\phi (\mathbf {v} )={\sqrt {\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}}}}$
• Inverse multiquadratics: ${\displaystyle \,\phi (\mathbf {v} )=\left(\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}\right)^{-{\frac {1}{2}}}}$
• Polyharmonic splines

where ${\displaystyle \mathbf {c} }$ is the vector representing the function center and ${\displaystyle a}$ and ${\displaystyle \sigma }$ are parameters affecting the spread of the radius.

A computationally efficient radial basis function has been proposed,[4] called Square-law based RBF kernel (SQ-RBF) which eliminates the exponential term as found in Gaussian RBF.

• SQ-RBF: ${\displaystyle f(\mathbf {v} )={\begin{cases}1-{\frac {1}{2}}\|\mathbf {v} -\mathbf {c} \|^{2}&:\|\mathbf {v} -\mathbf {c} \|\leq 1\\{\frac {1}{2}}(2-\|\mathbf {v} -\mathbf {c} \|)^{2}&:1\leq \|\mathbf {v} -\mathbf {c} \|\leq 2\\0&:\|\mathbf {v} -\mathbf {c} \|\geq 2.\end{cases}}}$

Folding activation functions

Folding activation functions are extensively used in the pooling layers in convolutional neural networks, and in output layers of multiclass classification networks. These activations perform aggregation over the inputs, such as taking the mean, minimum or maximum. In multiclass classification the softmax activation is often used.

Comparison of activation functions

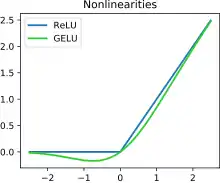
There are numerous activation functions. Hinton et al.'s seminal 2012 paper on automatic speech recognition uses a logistic sigmoid activation function.[5] The seminal 2012 AlexNet computer vision architecture uses the ReLU activation function, as did the seminal 2015 computer vision architecture ResNet. The seminal 2018 language processing model BERT uses a smooth version of the ReLU, the GELU.[6]

Aside from their empirical performance, activation functions also have different mathematical properties:

Nonlinear

When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator.[7] This is known as the Universal Approximation Theorem. The identity activation function does not satisfy this property. When multiple layers use the identity activation function, the entire network is equivalent to a single-layer model.

Range

When the range of the activation function is finite, gradient-based training methods tend to be more stable, because pattern presentations significantly affect only limited weights. When the range is infinite, training is generally more efficient because pattern presentations significantly affect most of the weights. In the latter case, smaller learning rates are typically necessary.

Continuously differentiable

This property is desirable (ReLU is not continuously differentiable and has some issues with gradient-based optimization, but it is still possible) for enabling gradient-based optimization methods. The binary step activation function is not differentiable at 0, and it differentiates to 0 for all other values, so gradient-based methods can make no progress with it.[8]

Monotonic

When the activation function is monotonic, the error surface associated with a single-layer model is guaranteed to be convex.[9]

Smooth functions with a monotonic derivative

These have been shown to generalize better in some cases.

Approximates identity near the origin

When activation functions have this property, the neural network will learn efficiently when its weights are initialized with small random values. When the activation function does not approximate identity near the origin, special care must be used when initializing the weights.[10] In the table below, activation functions where ${\displaystyle f(0)=0}$ and ${\displaystyle f'(0)=1}$ and ${\displaystyle f'}$ is continuous at 0 are indicated as having this property.

These properties do not decisively influence performance, nor are they the only mathematical properties that may be useful. For instance, the strictly positive range of the softplus makes it suitable for predicting variances in variational autoencoders.

The following table compares the properties of several activation functions that are functions of one fold x from the previous layer or layers:

Name	Plot	Function, ${\displaystyle f(x)}$	Derivative of ${\displaystyle f}$, ${\displaystyle f'(x)}$	Range	Order of continuity	Mono­tonic	Monotonic derivative	Approximates identity near the origin
Identity		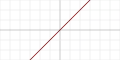${\displaystyle x}$	${\displaystyle 1}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{\infty }}$	Yes	Yes	Yes
Binary step		${\displaystyle {\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle {\begin{cases}0&{\text{if }}x\neq 0\\{\text{undefined}}&{\text{if }}x=0\end{cases}}}$	${\displaystyle \{0,1\}}$	${\displaystyle C^{-1}}$	Yes	No	No
Logistic, sigmoid, or soft step		${\displaystyle \sigma (x)={\frac {1}{1+e^{-x}}}}$	${\displaystyle f(x)(1-f(x))}$	${\displaystyle (0,1)}$	${\displaystyle C^{\infty }}$	Yes	No	No
tanh		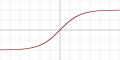${\displaystyle \tanh(x)={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$	${\displaystyle 1-f(x)^{2}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{\infty }}$	Yes	No	Yes
Rectified linear unit (ReLU)[11]		${\displaystyle {\begin{aligned}&{\begin{cases}0&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}\\{}={}&\max\{0,x\}=x{\textbf {1}}_{x>0}\end{aligned}}}$	${\displaystyle {\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x>0\\{\text{undefined}}&{\text{if }}x=0\end{cases}}}$	${\displaystyle [0,\infty )}$	${\displaystyle C^{0}}$	Yes	Yes	No
Gaussian error linear unit (GELU)[6]		${\displaystyle {\begin{aligned}&{\frac {1}{2}}x\left(1+{\text{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right)\\{}={}&x\Phi (x)\end{aligned}}}$	${\displaystyle \Phi (x)+x\phi (x)}$	${\displaystyle (-0.17\ldots ,\infty )}$	${\displaystyle C^{\infty }}$	No	No	No
Softplus[12]		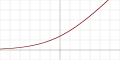${\displaystyle \ln \left(1+e^{x}\right)}$	${\displaystyle {\frac {1}{1+e^{-x}}}}$	${\displaystyle (0,\infty )}$	${\displaystyle C^{\infty }}$	Yes	Yes	No
Exponential linear unit (ELU)[13]		${\displaystyle {\begin{cases}\alpha \left(e^{x}-1\right)&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}}$ with parameter ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x>0\\1&{\text{if }}x=0{\text{ and }}\alpha =1\end{cases}}}$	${\displaystyle (-\alpha ,\infty )}$	${\displaystyle {\begin{cases}C^{1}&{\text{if }}\alpha =1\\C^{0}&{\text{otherwise}}\end{cases}}}$	Iff ${\displaystyle \alpha \geq 0}$	Iff ${\displaystyle 0\leq \alpha \leq 1}$	Iff ${\displaystyle \alpha =1}$
Scaled exponential linear unit (SELU)[14]		${\displaystyle \lambda {\begin{cases}\alpha (e^{x}-1)&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$ with parameters ${\displaystyle \lambda =1.0507}$ and ${\displaystyle \alpha =1.67326}$	${\displaystyle \lambda {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\lambda \alpha ,\infty )}$	${\displaystyle C^{0}}$	Yes	No	No
Leaky rectified linear unit (Leaky ReLU)[15]		${\displaystyle {\begin{cases}0.01x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle {\begin{cases}0.01&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$	Yes	Yes	No
Parameteric rectified linear unit (PReLU)[16]		${\displaystyle {\begin{cases}\alpha x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$ with parameter ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha &{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$	Iff ${\displaystyle \alpha \geq 0}$	Yes	Iff ${\displaystyle \alpha =1}$
ElliotSig,[17][18] softsign[19][20]		${\displaystyle {\frac {x}{1+|x|}}}$	${\displaystyle {\frac {1}{(1+|x|)^{2}}}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{1}}$	Yes	No	Yes
Square nonlinearity (SQNL)[21]		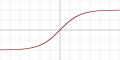${\displaystyle {\begin{cases}1&{\text{if }}x>2.0\\x-{\frac {x^{2}}{4}}&{\text{if }}0\leq x\leq 2.0\\x+{\frac {x^{2}}{4}}&{\text{if }}-2.0\leq x<0\\-1&{\text{if }}x<-2.0\end{cases}}}$	${\displaystyle 1\mp {\frac {x}{2}}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{1}}$	Yes	No	Yes
S-shaped rectified linear activation unit (SReLU)[22]		${\displaystyle {\begin{cases}t_{l}+a_{l}(x-t_{l})&{\text{if }}x\leq t_{l}\\x&{\text{if }}t_{l}<x<t_{r}\\t_{r}+a_{r}(x-t_{r})&{\text{if }}x\geq t_{r}\end{cases}}}$ where ${\displaystyle t_{l},a_{l},t_{r},a_{r}}$ are parameters.	${\displaystyle {\begin{cases}a_{l}&{\text{if }}x\leq t_{l}\\1&{\text{if }}t_{l}<x<t_{r}\\a_{r}&{\text{if }}x\geq t_{r}\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$	No	No	No
Bent identity		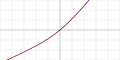${\displaystyle {\frac {{\sqrt {x^{2}+1}}-1}{2}}+x}$	${\displaystyle {\frac {x}{2{\sqrt {x^{2}+1}}}}+1}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{\infty }}$	Yes	Yes	Yes
Sigmoid linear unit (SiLU,[6] SiL,[23] or Swish-‍1[24])		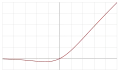${\displaystyle {\frac {x}{1+e^{-x}}}}$	${\displaystyle {\frac {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}}$	${\displaystyle [-0.278\ldots ,\infty )}$	${\displaystyle C^{\infty }}$	No	No	For ${\displaystyle 2f(x)}$
Gaussian		${\displaystyle e^{-x^{2}}}$	${\displaystyle -2xe^{-x^{2}}}$	${\displaystyle (0,1]}$	${\displaystyle C^{\infty }}$	No	No	No
SQ-RBF		${\displaystyle {\begin{cases}1-{\frac {x^{2}}{2}}&{\text{if }}|x|\leq 1\\{\frac {1}{2}}(2-|x|)^{2}&{\text{if }}1<|x|<2\\0&{\text{if }}|x|\geq 2\end{cases}}}$	${\displaystyle {\begin{cases}-x&{\text{if }}|x|\leq 1\\x-2\operatorname {sgn}(x)&{\text{if }}1<|x|<2\\0&{\text{if }}|x|\geq 2\end{cases}}}$	${\displaystyle [0,1]}$	${\displaystyle C^{0}}$	No	No	No

^ Here, ${\displaystyle \sigma }$ is the logistic function.

^ ${\displaystyle \alpha >0}$ for the range to hold true.

The following table lists activation functions that are not functions of a single fold x from the previous layer or layers:

Name	Equation, ${\displaystyle f_{i}\left({\vec {x}}\right)}$	Derivatives, ${\displaystyle {\frac {\partial f_{i}\left({\vec {x}}\right)}{\partial x_{j}}}}$	Range	Order of continuity
Softmax	${\displaystyle {\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}}$    for i = 1, …, J	${\displaystyle f_{i}\left({\vec {x}}\right)\left(\delta _{ij}-f_{j}\left({\vec {x}}\right)\right)}$	${\displaystyle (0,1)}$	${\displaystyle C^{\infty }}$
Maxout[25]	${\displaystyle \max _{i}x_{i}}$	${\displaystyle {\begin{cases}1&{\text{if }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{if }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$
FReLU[26]	${\displaystyle \max(x_{c,i,j},x_{c,i,j}^{\omega }\cdot p_{c}^{\omega })}$		${\displaystyle (-\infty ,\infty )}$

^ Here, ${\displaystyle \delta _{ij}}$ is the Kronecker delta.

^ For instance, ${\displaystyle j}$ could be iterating through the number of kernels of the previous neural network layer while ${\displaystyle i}$ iterates through the number of kernels of the current layer.

See also

• Logistic function
• Rectifier (neural networks)
• Stability (learning theory)
• Softmax function

References

1. Hinkelmann, Knut. "Neural Networks, p. 7" (PDF). University of Applied Sciences Northwestern Switzerland.
2. Hodgkin, A. L.; Huxley, A. F. (1952-08-28). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–544. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
3. Behnke, Sven (2003). Hierarchical Neural Networks for Image Interpretation. Lecture Notes in Computer Science. 2766. Springer. doi:10.1007/b11963. ISBN 978-3-540-40722-5. S2CID 1304548.
4. Wuraola, Adedamola; Patel, Nitish (2018), "Computationally Efficient Radial Basis Function", 2018 International Conference on Neural Information Processing (ICONIP), Siem reap Cambodia: Springer, pp. 103–112, doi:10.1007/978-3-030-04179-3_9
5. Hinton, Geoffrey; Deng, Li; Deng, Li; Yu, Dong; Dahl, George; Mohamed, Abdel-rahman; Jaitly, Navdeep; Senior, Andrew; Vanhoucke, Vincent; Nguyen, Patrick; Sainath, Tara; Kingsbury, Brian (2012). "Deep Neural Networks for Acoustic Modeling in Speech Recognition". Cite journal requires |journal= (help)
6. Hendrycks, Dan; Gimpel, Kevin (2016). "Gaussian Error Linear Units (GELUs)". arXiv:1606.08415 [cs.LG].
7. Cybenko, G. (December 1989). "Approximation by superpositions of a sigmoidal function". Mathematics of Control, Signals, and Systems. 2 (4): 303–314. doi:10.1007/BF02551274. ISSN 0932-4194. S2CID 3958369.
8. Snyman, Jan (3 March 2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Science & Business Media. ISBN 978-0-387-24348-1.
9. Wu, Huaiqin (2009). "Global stability analysis of a general class of discontinuous neural networks with linear growth activation functions". Information Sciences. 179 (19): 3432–3441. doi:10.1016/j.ins.2009.06.006.
10. Sussillo, David; Abbott, L. F. (2014-12-19). "Random Walk Initialization for Training Very Deep Feedforward Networks". arXiv:1412.6558 [cs.NE].
11. Nair, Vinod; Hinton, Geoffrey E. (2010), "Rectified Linear Units Improve Restricted Boltzmann Machines", 27th International Conference on International Conference on Machine Learning, ICML'10, USA: Omnipress, pp. 807–814, ISBN 9781605589077
12. Glorot, Xavier; Bordes, Antoine; Bengio, Yoshua (2011). "Deep sparse rectifier neural networks" (PDF). International Conference on Artificial Intelligence and Statistics.
13. Clevert, Djork-Arné; Unterthiner, Thomas; Hochreiter, Sepp (2015-11-23). "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". arXiv:1511.07289 [cs.LG].
14. Klambauer, Günter; Unterthiner, Thomas; Mayr, Andreas; Hochreiter, Sepp (2017-06-08). "Self-Normalizing Neural Networks". Advances in Neural Information Processing Systems. 30 (2017). arXiv:1706.02515. Bibcode:2017arXiv170602515K.
15. Maas, Andrew L.; Hannun, Awni Y.; Ng, Andrew Y. (June 2013). "Rectifier nonlinearities improve neural network acoustic models". Proc. ICML. 30 (1). S2CID 16489696.
16. He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015-02-06). "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification". arXiv:1502.01852 [cs.CV].
17. Elliot, David L. (1993), "A better activation function for artificial neural networks", ISR Technical Report TR 93-8, University of Maryland, College Park, MD 20742., CiteSeerX 10.1.1.46.7204
18. "elliotsig, Elliot symmetric sigmoid transfer function", command introduced in Matlab R2012b, Matlab Documentation, MathWorks.
19. Bergstra, James; Desjardins, Guillaume; Lamblin, Pascal; Bengio, Yoshua (2009). "Quadratic polynomials learn better image features". Technical Report 1337". Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Archived from the original on 2018-09-25.
20. Glorot, Xavier; Bengio, Yoshua (2010), "Understanding the difficulty of training deep feedforward neural networks" (PDF), International Conference on Artificial Intelligence and Statistics (AISTATS'10), Society for Artificial Intelligence and Statistics
21. Wuraola, Adedamola; Patel, Nitish (2018), "SQNL:A New Computationally Efficient Activation Function", 2018 International Joint Conference on Neural Networks (IJCNN), Rio Rio de Janeiro, Brazil: IEEE, pp. 1–7
22. Jin, Xiaojie; Xu, Chunyan; Feng, Jiashi; Wei, Yunchao; Xiong, Junjun; Yan, Shuicheng (2015-12-22). "Deep Learning with S-shaped Rectified Linear Activation Units". arXiv:1512.07030 [cs.CV].
23. Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji (2018). "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning". Neural Networks. 107: 3–11. arXiv:1702.03118. doi:10.1016/j.neunet.2017.12.012. PMID 29395652. S2CID 6940861.
24. Ramachandran, Prajit; Zoph, Barret; Le, Quoc V (2017). "Searching for Activation Functions". arXiv:1710.05941 [cs.NE].
25. Goodfellow, Ian J.; Warde-Farley, David; Mirza, Mehdi; Courville, Aaron; Bengio, Yoshua (2013). "Maxout Networks". JMLR Workshop and Conference Proceedings. 28 (3): 1319–1327. arXiv:1302.4389. Bibcode:2013arXiv1302.4389G.
26. Ma, Ningning. "Funnel Activation for Visual Recognition". ECCV 2020. 12356: 351–368. arXiv:2007.11824. doi:10.1007/978-3-030-58621-8_21.