6-6 duoprism

In geometry of 4 dimensions, a 6-6 duoprism or hexagonal duoprism is a polygonal duoprism, a 4-polytope resulting from the Cartesian product of two hexagons.

Uniform 6-6 duoprism

Schlegel diagram
TypeUniform duoprism
Schläfli symbol{6}×{6} = {6}2
Coxeter diagrams
Cells12 hexagonal prisms
Faces36 squares,
12 hexagons
Edges72
Vertices36
Vertex figureTetragonal disphenoid
Symmetry[[6,2,6]] = [12,2+,12], order 288
Dual6-6 duopyramid
Propertiesconvex, vertex-uniform, facet-transitive

It has 36 vertices, 72 edges, 48 faces (36 squares, and 12 hexagons), in 12 hexagonal prism cells. It has Coxeter diagram , and symmetry [[6,2,6]], order 288.

Images


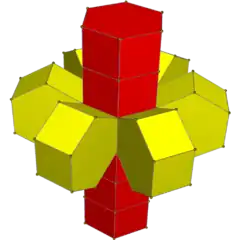
Net

Seen in a skew 2D orthogonal projection, it contains the projected rhombi of the rhombic tiling.

6-6 duoprism Rhombic tiling
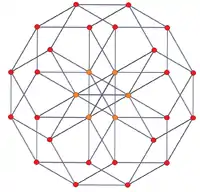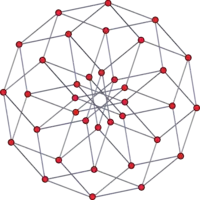6-6 duoprism 6-6 duoprism
Orthogonal projection shows 6 red and 6 blue outlined 6-edges

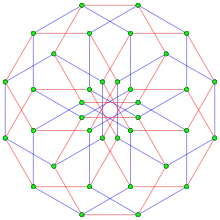
The regular complex polytope 6{4}2, , in has a real representation as a 6-6 duoprism in 4-dimensional space. 6{4}2 has 36 vertices, and 12 6-edges. Its symmetry is 6[4]2, order 72. It also has a lower symmetry construction, , or 6{}×6{}, with symmetry 6[2]6, order 36. This is the symmetry if the red and blue 6-edges are considered distinct.[1]

6-6 duopyramid
6-6 duopyramid
TypeUniform dual duopyramid
Schläfli symbol{6}+{6} = 2{6}
Coxeter diagrams
Cells36 tetragonal disphenoids
Faces72 isosceles triangles
Edges48 (36+12)
Vertices12 (6+6)
Symmetry[[6,2,6]] = [12,2+,12], order 288
Dual6-6 duoprism
Propertiesconvex, vertex-uniform,
facet-transitive

The dual of a 6-6 duoprism is called a 6-6 duopyramid or hexagonal duopyramid. It has 36 tetragonal disphenoid cells, 72 triangular faces, 48 edges, and 12 vertices.

It can be seen in orthogonal projection:

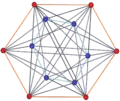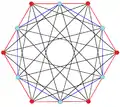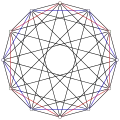Skew [6] [12]
Orthographic projection

The regular complex polygon 2{4}6 or has 12 vertices in with a real representation in matching the same vertex arrangement of the 6-6 duopyramid. It has 36 2-edges corresponding to the connecting edges of the 6-6 duopyramid, while the 12 edges connecting the two hexagons are not included.

The vertices and edges makes a complete bipartite graph with each vertex from one pentagon is connected to every vertex on the other.[2]

The 3-3 duoantiprism is an alternation of the 6-6 duoprism, but is not uniform. It has a highest symmetry construction of order 144 uniquely obtained as a direct alternation of the uniform 6-6 duoprism with an edge length ratio of 0.816 : 1. It has 30 cells composed of 12 octahedra (as triangular antiprisms) and 18 tetrahedra (as tetragonal disphenoids). The vertex figure is a gyrobifastigium, which has a regular-faced variant that is not isogonal. It is also the convex hull of two uniform 3-3 duoprisms in opposite positions.


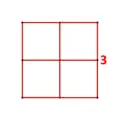
Vertex figure for the 3-3 duoantiprism

See also

Notes
  1. Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
  2. Regular Complex Polytopes, p.114

References
  • Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
  • Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
    • Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
    • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • Catalogue of Convex Polychora, section 6, George Olshevsky.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.